Keresse a kiskorúak és kofaktorokat elemeinek az alfa - dokumentum - oldal
Keresse a kiskorúak és algebrai α12 elemek kiegészítések. α32. Számítsuk determináns: a) kiterjesztve azt az elemek az első sor és a második oszlopon; b) befogadja az a előgyártmány nullák az első sorban.
Szóba jöhető elemek A12 és A32 rendre:
a) számítjuk a meghatározó, kiterjesztve azt a elemei az első sorban:
+ = 1-3 (8 + 2 + 4 - 4) - 2 (- 8 - 16 + 6 + 12 + 4 - 16) + (16 - 12 - - 4 + 32) = 38;
Bővítjük meghatározó elemei által a második oszlop:
= - 2 - 2 + 1 = - 2 (- 8 + 6 - 16 + + 12 + 4 - 16) - 2 (12 + 6 - 6 - 16) + (- 6 + 16 - 12 - 4) = 38;
b) kiszámítjuk a vett előre nullák az első sorban. Mi használjuk a megfelelő tulajdonságát meghatározó. Megszorozva a harmadik oszlop 3 meghatározó, és adjunk hozzá, hogy az első, majd szorozza -2 és hozzá a második. Ezután, az első sorban az összes elemet, egy kivételével, nulla lesz. Felbontjuk így kapott meghatározó elemei által az első sor és számítsuk ki:
(A meghatározója a harmadik rend kapott nullák az első oszlopban az ugyanaz, mint a fenti tulajdonságokat determinánsok.) ◄
Adott egy lineáris inhomogén algebrai egyenletek
Ellenőrizze, hogy a rendszer koherenciáját, abban az esetben a kompatibilitás megoldani: a) a Cramer-szabály; b) a fordított mátrix (mátrix módszer); c) a Gauss módszer.
►Sovmestnost a rendszer ellenőrzést egy tétele Kronecker - Capelli. Elemi transzformációk megtalálják a rangot a mátrix
Ez a rendszer, és a rangot a kibővített mátrix
Ehhez, megszorozzuk az első sorban a mátrix B 2 és adja ki egy második, majd szorozzuk az első sor a -3, és adjunk hozzá egy harmadik, az adatcsere a második és harmadik oszlop. megkapjuk
Következésképpen, csengett A = Rang B = 3 (t. E. A ismeretlenek száma). Tehát az eredeti rendszer következetes és egyedi megoldás.
a) a Cramer szabály
b) a megoldásokat találjanak a rendszer használatával a fordított mátrixba levelet az egyenletrendszert mátrix formában, mint Ax =. Megoldás A rendszer mátrix formában x = A-1. A képlet szerint találunk a fordított mátrixba A-1 (amely létezik, mivel a = det A = - 16 ≠ 0):
c) Oldjuk a rendszer a Gauss módszer. X kizárják a második és a harmadik egyenlet. Ebből a célból az első egyenletben megszorozzuk 2 és vonjuk a második, majd megszorozzuk az első egyenlet 3 és vonjuk ki a harmadik:
A kapott rendszer lelet X = - 4, y = 1, z = -2. ◄
A tetejét a piramisok pontokon A (2; 3; 4), B (4, 7, 3), C (1, 2, 2) és a D (- 2, 0, - 1). Számítsuk: a) azon felületének ABC; b) a keresztmetszeti területe, közepén áthaladó az AB bordák. AC. AD; c) a térfogata ABCD piramis.
►a) Ismeretes, hogy SABC =. Azt találjuk: = (2; 4; - 1)
b) Közép-AB bordák. BC és AD találhatók pontok (3; 5; 3,5)
Az erő F = (2; 3 - 5) alkalmazva, hogy a pont A (február 01-02). Számítsuk: a) a működési F erő, ha a pont az alkalmazás, mozgó egyenes vonalban mozog a helyzetben az A a B pozíció (1; 4; 0); b) egy egységet pillanatában F erő tekintetében pont B.
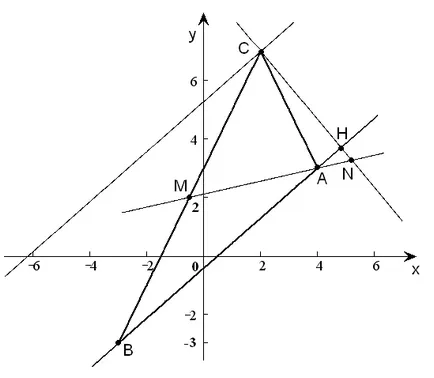
Ismert csúcsok G (0, 0), A (- 2, 0) a paralelogramma OASD és a metszéspont a átlók a (2; -2). Írja az egyenletek a paralelogramma oldalai.
►Uravnenie használt OA lehet írva egyszerre: y = 0. Továbbá, mivel a B pont az a felezőpontja az átlós AD (. 1. ábra), elosztjuk a szegmens két képlet tudja számítani a koordinátáit a vertex D (x; y):
Most már meg az egyenleteket összes többi felet. Figyelembe véve a párhuzamosság az OA és a CD irányban. Alkotunk az egyenlet CD oldalon: y = -4. Az egyenlet OD oldalán készült két ismert pontok:
Végül találunk az egyenlet AC oldal. tekintettel arra a tényre. hogy áthalad egy ismert pont (- 2, 0) párhuzamosan ismert közvetlen OD:
a) egyenlet AB oldali;
b) az egyenlet magasság CH;
b) a medián egyenlet AM;
g) a metszéspontja N AM és átlagos magasságuk CH;
e) az egyenlet a vonal áthalad a vertex C párhuzamos AB oldal;
e) a távolság a C pont, hogy a vonal AB.
►a) egyenletet használva az egyenes átmenő két pontot. megkapjuk az egyenlet AB oldalán:
b) Az egyenlet szerint
c) A jól ismert képletekkel találunk koordinátáit x. y a középső M a szegmens BC:
Most két ismert pont, A és M forma az egyenlet medián AM:
g), hogy megtalálja a koordinátáit a metszéspontja N AM és átlagos magasságuk CH össze az egyenletrendszert
Megoldására, megkapjuk N (26/5; 49/15);
d) Mivel a vonal áthalad a C csúcs párhuzamos az AB oldal. ezek szögletes együtthatók k1 = 6/7. Ezután a következő egyenlet szerint:
e) A távolság a C pont, hogy a vonal AB kiszámítása az ismert képlet:
A megoldás erre a problémára ábrán mutatjuk be. 2. ◄
►a) A sík egyenlete segítségével három pontot. képezik az egyenlet A1A2A3 sík:
ahol 6x - 7V - 9Z + 97 = 0;
b) Figyelembe véve az egyenlet a vonal áthalad a két pontot. A1A2 közvetlen egyenlet felírható
c) A feltétele merőlegességi pryamoyA4Mi ploskostiA1A2A3 az következik, hogy az az irány vektort a vonal s vehet a normál vektor n = (6 - 7 - 9) A1A2A3 síkban. Ekkor az egyenlet a sor A4M figyelembevételével kanonikus egyenletek egy egyenes vonal felírható
d) A képlet szerint a megállapítás közötti szög az egyenes vonal és a sík
e) képlet szerinti megtalálni a szöget a síkok közötti
Az egyenlet a áthaladó sík M pont (4; 3; 1) és
N (- 2, 0, - 1), amely párhuzamos a húzott pontokon keresztül Egy (1, 1, - 1) és
►Soglasno képletű egyenes egyenletek a térben. áthaladó két pont, egyenes egyenlet formájában AB
Ha a sík átmegy az M pont (4; 3; 1). az egyenlet lehet írva, mint a (X- 4) + B (y- 3) + C (Z- 1) = 0. Mivel ebben a síkban, és áthalad ponton N (- 2, 0, - 1). akkor a feltétel
A (- 2 - 4) + B (0 - 3) + C (- 1 - 1) = 0, vagy 6A + 3B + 2C = 0.
Mivel a kívánt sík párhuzamos az AB talált. tehát az a feltételeket, a képletek a párhuzamos vonalak és síkok, van:
-4A + 0B + 1C = 0 vagy 4A - C = 0.
találják, hogy a C = 4A, B = -A. Behelyettesítve a értékei a C és B a kívánt síkban egyenletet, megkapjuk
Mivel A ≠ 0 a kapott egyenlet egyenértékű az egyenlet
3 (x - 4) - 14 (y - 3) + 12 (Z - 1) = 0. ◄
►Zapishem paraméteres egyenletek az egyenes M1M2. erre a síkra merőleges: X = 6 + t, y = - 4 + T, Z = - 2 + t. Megoldása őket az egyenlet adott síkban, megkapjuk t = 1, és ezáltal közvetlen M1M2 metszéspontja M e sík: M (7 - 3; - 1). Mivel az M pont a középpontját a szegmens M1M2. A valódi egyenlőség
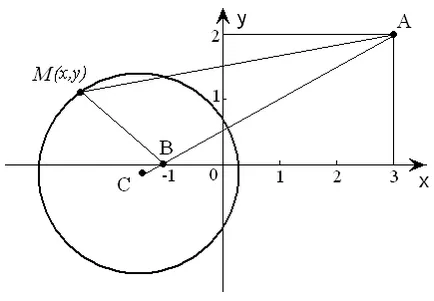
A vonal egyenlete, minden pontja M amely bizonyos távolságra van pont
A (3, 2) a parttól háromszor nagyobb, mint a B pontból (- 1, 0).
►Pust M (x; y) - minden egyes pontja a kívánt sort (3. ábra). Ezután a feltétel a probléma | DE | = 3 | BM | . mert
akkor az egyenlet a szükséges vonal
Mi átalakítja azt felemelt mindkét oldalán a tér. Van:
Kiemelve a teljes négyzetek az utolsó egyenletet, megkapjuk az egyenlet formájában
amely az egyenlet a kör középpontja pontban
Készítsen kanonikus egyenletek: a) egy ellipszis, a fél nagytengely a egyenlő 3. A hangsúly pont F (0); b) a képzetes tengelyének a hiperbola, a hangsúly a 2. és F (-, 0); c) olyan parabolát jelent, amelynek direktrix x = -3.
►a) kanonikus egyenlet formájában egy ellipszis. Nyilatkozata szerint a probléma félig főtengelye a = 3, p =. Egy ellipszis, az egyenlőség
b) A kanonikus egyenlet formájában hiperbola. A hipotézis képzetes tengelyük b = 2 és c =. Mert túlzás egyenlőség b2 = c2-a2. Ezért a2 = c2-b2 = () 2- 22 = 9. Write kívánt hiperbola egyenlete:
c) A kanonikus egyenlete a parabola ebben az esetben kell az űrlap y2 = 2px. és annak direktrix egyenlete x = - p / 2. De állapot egyenlet probléma direktrix x = - 3. Ezért - p / 2 = - p = 3 6, és a szükséges kanonikus egyenlet formájában parabola
Kapcsolódó dokumentumok:
meghatározó naytiminory és algebraicheskiedopolneniyaelementov AI2. ez az elem i-edik sorának. 3; 7; -5), B (2, -4, 1). 7. feladat Tekintettel két vektor: = <8; 4; 1>, = <2;–2; 1>. Keresse vektor. és egy síkban vektorok. merőleges a vektorba.
találni egy négyzetes mátrix) minorelementa; b) algebraicheskoedopolnenieelementa; c). Találd) minorelementa; b) algebraicheskoedopolnenieelementa; c) a meghatározó, a technika nullák az első sorban. Megoldás a) Minoromelementa.
elem mátrix. " Definíció. Algebraicheskimdopolneniemelementa aіk mátrix nevezzük Minor MIK ez a mátrix szorozva (-1) és a +: Algebraicheskoedopolnenieelementa. módszer. 1. példa megkeresni az adott mátrix det A. Megoldás. Transform.
edik oszlop; úgynevezett minoromelementa. Aztán, definíció szerint, helység (1) - algebraicheskoedopolnenieelementa. majd (2). Lineáris műveleteket mátrixok feladat. Keresse meg az összeget a matricát és a termék. kompatibilis, arra van szükség, hogy megtalálja a megfelelő általános megoldást.
Ez meghatározó hívják minoromelementa aij. Kijelölt Minor - Mij. Példa: A Naytiminorelementa determináns a12. egységnyi alábbi Minor: Algebraicheskimdopolneniemelementa meghatározó hívják annak csekély venni vele.