Keresse időközönként növekedését és csökkenését a származtatott funkciók CSE

\ (\ Blacktriangleright \) Ha a derivált pozitív intervallumban \ ((a; b) \). A funkció szigorúan növekszik. \ (F „(x)> 0 \ Longrightarrow f (x) \ uparrow \)

Ha a származék negatív intervallumban \ ((a; b) \). A funkció szigorúan csökkenő. \ (F „(x)<0 \Longrightarrow f(x) \downarrow\)

Megjegyezzük, hogy az ellenkezője nem igaz. Azaz, ha a függvény szigorúan növekvő néhány intervallum, akkor ebből nem következik, hogy minden ebben az időszakban a deriváltja pozitív. Például:

függvény \ (f (x) = x ^ 3 \) időközzel \ ([- 1; 1] \) szigorúan növekszik, de a-származék nem pozitív mindenhol: a \ (x = 0 \) származéka \ (f ' (0) = 0 \) (például a \ (f „(x) = 3x ^ 2 \)).

\ (\ Blacktriangleright \) Ha a függvény nem csökken (növekedés és / vagy állandó) intervallumban \ ((a, b) \). akkor ezen az intervallumon deriváltja nem-negatív (\ (\ GEQ 0 \)). Az ellenkezője igaz.

\ (\ Blacktriangleright \) Ha a funkció nemnövekv® (csökkenésével és / vagy állandó) intervallumban \ ((a, b) \). akkor ezen az intervallumon deriváltja nem pozitív (\ (\ leq 0 \)). Az ellenkezője igaz.

\ (\ Blacktriangleright \) a pontokon a törés (az ábrán ezt a pontot \ (A \) és \ (B \)) származéka nem létezik.

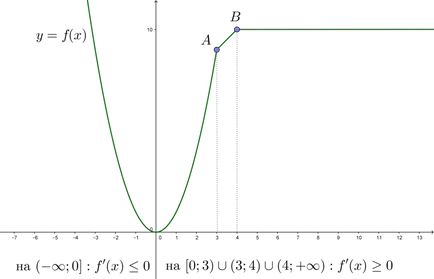
Megjegyezzük, hogy az intervallum \ ((4; + \ infty) \) származékot \ (f „(x) = 0 \). mert ebben az intervallumban egy konstans függvényt (\ (f (x) = 10 \)).

Példa: kap a pontok száma, ahol a származék egyenlő nulla, ha a ábra egy grafikon, jellemzői:

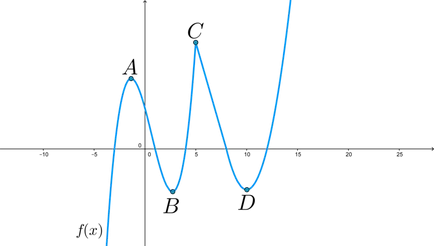
A származék nulla pontok \ (A, B, D \). és azon a ponton \ (C \) nem létezik, hiszen az a pont a törés.

Végső munka formájában EGE 11 osztályosok feltétlenül hivatkozást tartalmaz számítani korlátok és hiányosságok csökkenő növekvő differenciálhányados, a keresés a extrémuma pontot és nyomtatás. Jól ismeri a téma lehetővé teszi, hogy helyesen válaszolni néhány teszt kérdésekre, és nem tapasztal problémákat a szakmai továbbképzés.

Alapjai differenciálszámítás - az egyik fő témája a modern iskolában a matematika. Tanul a használata származékok a tanulmány a függő változó - az a származék lehet elemezni növekedését és csökkenését funkció hivatkozás nélkül a rajz.

Komplex készítmény diplomások át a vizsgán az oktatási portál „Shkolkovo” lesz mélyen megérteni az elveket a differenciálás - részletesen megérteni az elméletet, hogy tanulmányozza a példák megoldása a közös feladatok, és próbálja meg a kezét önálló munkát. Segíthetünk töltse ki a hézagokat tudás - meghatározására, hogy a lexikális fogalmakat és témákat a függő változók. A tanulók képesek lesznek megismételni, hogyan kell megtalálni monotónia időközönként, ami azt jelenti, az emelkedés vagy csökkenés differenciálhányados egy bizonyos intervallumban, amikor a végpontok is beletartoznak, amelyek nem tartoznak az eredményeket időközönként.

A választás a szakasz „kivitelező”, a hallgatók képesek lesznek gyakorolni a tanulmány a növekedés és csökkenés differenciálhányados az igazi vizsga változat folyamatosan frissül a legújabb változások és újítások.