Kinematikája egy merev test
Abszolút szilárd test törzsének nevezzük, amikor a vezetés közötti távolság két fix pont nem változik. A szilárd test lehet a kétféle - transzlációs és rotációs.
Amikor az előre mozgó bármelyik vonal mereven kapcsolódik a testtel párhuzamos marad az eredeti irányba és pályája bármely két kapcsolódó szervezet, pontok azonosak (ezek teljes mértékben igazítsa párhuzamos fordítás). Egy példa a transzlációs mozgást a talajhoz képest lehet a felvonó autó, „óriáskerék” utastérbe, iránytű egy tetszőleges mozgó testét vízszintes irányban, stb
Az előre irányuló mozgás növekménye a sugár vektorok az összes pixel azonos szilárd test, ezért ugyanazzal a sebességgel és a gyorsulás. Következésképpen transzlációs merev test mozgása által leírt kinematikai egyenletek, annak bármely pont.
Ha a merev test forgása két A és B pontok álló helyzetben marad, akkor bármely C. pontjában feküdt egy egyenes vonal AB is rögzítve van. Ha a C pont mozog, az AC és BC hosszúságú szegmenst változások, ami ellentmond a meghatározása a merev test. Egy egyenes, amely átmegy a szegmens AB nevezzük a forgástengely. egy merev test mozgása nevezik a test forgását körülbelül egy rögzített tengely.
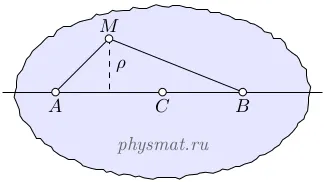
Ábra. 1 Abszolút szilárd
Tekintsünk egy tetszőleges pontja M a test nem illeszkedik a forgástengely AB (1. ábra). Mivel a szegmensek hossza MA. MB és az MN. ahol N metszéspontja merőleges csökkent az M pont a tengelyen AB. mozgás közben állandó marad, akkor az összes pontot a forgó test leírja a körön p egyenlő a távolság a lényeg, hogy a forgástengely, merőleges síkban a tengelye körül forog. Egy példa a forgás mintegy egy rögzített tengely a rotor lehet egy elektromos motor, vagy turbina.
Ha egy merev test rögzített egy ponton, hogy állásfoglalásra nevezzük a test forgását egy rögzített pont körül. és az igen pont az úgynevezett forgási középpontja. Amikor egy ilyen mozgás meg tudja határozni a pillanatnyi forgástengely, mint a forgástengely közepén keresztül húzódó, és síkjára merőleges mozgás. A helyzet a pillanatnyi tengely viszonyítva a fix keret, és a szervezet maga is idővel változnak.
Ellentétben transzlációs mozgást, forgómozgást pont v sebességgel. található különböző távolságokban a forgástengely más lesz. Ezért során forgómozgás sebessége v az egyedi pont nem szolgálhat a kinematikai jellemző mozgást az egész test.
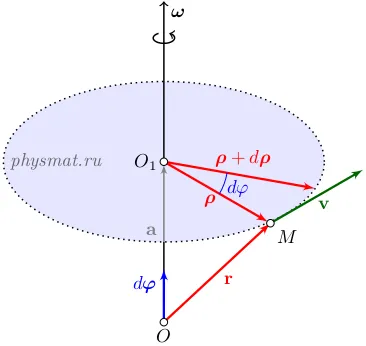
Ábra. 2 Forgatás merev test
Tekintsük a forgási mozgása a testet a forgásközépponti O OO1 pillanatnyi forgástengely. ahol a pont O1 megfelel a központ a körív, amely mozgatja az M pont (2. ábra). A sugár vektor az M pont tekintetében a forgási középpont O jelöli r. sugara vektor az M pont tekintetében O1 jelöljük ρ. és a vektor, a pont O pont O1 jelölésére. Ezeket a vektorokat a kapcsolódó által
A kis dt időintervallum ρ vektor forog a síkban a tengelyre merőleges OO1 szöget dφ. A sugár vektor bármely pontján a szilárd test (kivéve a pontokat a tengelyen, mivel a sugár vektor nulla) egy időben dt is elforgatja szögben dφ. különben ez azt eredményezné, hogy a változás, és a pontok közötti távolság, ami ellentmond a meghatározása merev test. Kiderült, hogy a forgatás szögét dφ jellemzi a forgómozgást a szervezetben. Bemutatjuk a vektor az elemi test forgásának (kis test forgása) dφ. számszerűen egyenlő a forgatási szög dφ és tengelyének irányába OO1. Az irány ezen vektor egybeesik azzal az iránnyal haladási elmondható, hogy a nyél együtt forog a test, azaz engedelmeskedik jobb kéz szabályt>.
A sorozat két elemi fordulat dφ1 és dφ2. vektor kívül engedelmeskedik a szabály, azaz sumarno elemi forgatás egyenlő egy fordulat
A változási sebességének a forgásszög φ nevezett skorostyuω szögsebességgel és definíció szerint, mint az arány a kis szög növekmény egy kis idő dt van:
A szögsebesség-vektora ω nagyságát jellemzi, és a változás iránya a kormányzási szöget. Ha a szögsebessége állandó ω = const. A mozgás az úgynevezett egységes körüli forgás rögzített tengely.
A sebesség v mozgásának egy pont M nevezzük lineáris sebesség. Amikor a test forog szögsebességgel ω egy időben dt M pont megy keresztül egy körív sugara ρ útvonal egyenlő DS. A lineáris sebesség
A 2. ábra azt mutatja, hogy a lineáris sebesség vektor merőleges a vektorok ω és ρ. és annak iránya egybeesik a vektorral terméket [ω. ρ]. Továbbá, a vektor ω és ρ kölcsönösen merőleges, így [ω. ρ] = ρω = v. ezért
Balra a vektor ω. Mint egy vektor ω kollineáris és keresztezett termék nulla, megkapjuk
Megvizsgáltuk a legáltalánosabb esetben a test forgásának képest egy fix pont - O. forgásközépponti Abban az esetben, ha a szervezet képest elfordul a rögzített tengely mint egy O pont lehet választani bármely pontján található, a forgástengely.
Jellemzésére egységes forgómozgást sorozatának alkalmazásával fogalmak.- vrascheniyaT időszakban nevezett időintervallumot, amelyre a egyenletesen forgó szögsebességgel ω szervezet látja egy teljes fordulatot, azaz elforgatható szögben φ = 2π.
- Vrascheniyaf frekvencia fordulatok számának a test, az 1 második egyenletes forgást szögsebességgel ω.
Ezeket a mennyiségeket a kapcsolódó következők:
Ha a test forog egyenletesen, majd bemutatjuk a jellemző változási sebessége szögsebesség - szögletes uskorenieε.
Abban az esetben, forgatás egy test egy rögzített tengely irányában szöggyorsulással vektor nem változik, de a változások csak a nagyságának. Ε szöggyorsulás vektor mentén irányul forgástengely irányában a szögsebesség, ha értéke pozitív (gyorsított elfordulás), valamint az ellenkező irányba az a szögsebesség, amikor értéke negatív (lassú forgatás).
Mi kifejezetten a tangenciális és a normál gyorsulás tetszőleges pontja M a test, körül forgó rögzített tengely a ferde jellemzők:
Vektor mennyiségek, a következő összefüggések:
Vegyünk néhány speciális esetben a szilárd test forgása:- egyenletes forgás
Transzlációs és rotációs mozgás egy merev test a legegyszerűbb típusú mozgás. Általában a szilárd végezhet összetett akaratlagos mozgás. Az az elméleti mechanika bebizonyosodik, hogy bármilyen bonyolult merev test mozgása tekinthető az összeg a transzlációs és rotációs mozgások.
Irodalom- AA Detlaf, BM Jaworski, LB Milkovskaya. Fizika persze. M. Higher School. 1973-tól.