Kinematikája és dinamikája a probléma

Fajlagos mechanikai energiaveszteség a súrlódás következtében a helyszínen élő szakaszok 1-1 és 2-2

Így a Bernoulli-egyenlet az elemi folyamok egy igazi folyadék esetében folyamatos mozgás is képviselteti magát

Jellemző a folyadék mozgása a fogalom a piezometrikus és hidraulikus gradiens.

Ábra. 3.8 ábra a görbék jellemzik a Bernoulli-egyenlet. Az átmenő pontot megfelelő piezometrikus magasságot életben szakaszok 1-1 és 2-2 piezometrikus sor.

Piezometrikus gradiens az úgynevezett változás hidrosztatikus nyomás vízfolyások mentén egységnyi hosszúságú. Hosszú adatfolyamok része közötti szakaszok 1-1 és 2-2 piezometrikus meredekség

Piezometrikus lejtőn megfelelő infinitezimális hossza (a), - előfeszítő pont:

Az átmenő pontértékeinek különleges mechanikai energia az élő szakaszok folyamok napornoyliniey (teljes vonal fej). Ez az úgynevezett hidraulikus gradiens csökkenése összes fajlagos mechanikus energia vízfolyások mentén egységnyi hossza:

Amikor egy elemi fajlagos energiafogyasztás csökkentése per infinitezimális rész hidraulikus gradiens

Mivel a teljes nyomás görbe mentén csökken a hossza áramok, a megjelölés expressziót (3,51) mínusz [- csökkenő függvény].

Abban az esetben, állandó keresztmetszetű hossza mentén élő stream piezometrikus vonal és a vonal párhuzamos a fej teljes.

3.9. Differenciálegyenletek MOTION ideális folyadék (Euler egyenlet)

A tér tele van mozgó ideális sűrűségű folyadékok lemerült elemi parallelepipedon, amelynek szélei az oldalaik párhuzamosak a koordináta-tengelyek (ábra. 3.9). Menet közben folyékony ideális nincs belső súrlódási erő. Volume elem, amely téglatest mozog abszolút sebesség. Az összetevői a sebesség mellett a koordináta tengelyek ,,.

Az elemi térfogat fogja alkalmazni a tömeg és felületi erők. A súrlódási erők mozgatásakor paralelepipedon nulla.

a folyékony massza egy elemi térfogata a paralelepipedon

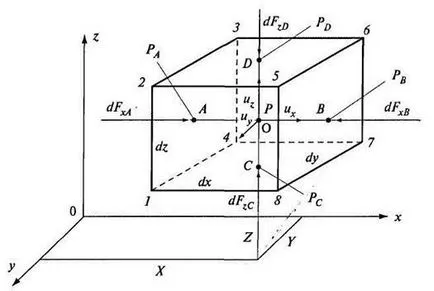
Ábra. 3.9. Származtatása az Euler-egyenlet a mozgás

A kiemelkedések a tömeg erők irányában a koordinátatengelyek:

ahol, - a komponensek egységnyi tömegű erők tengelyek körül (ezek a nyúlványok gyorsulási erők).

Felületi erők határozzák meg a nyomás tulajdonítható, hogy az arc a dobozból.

Tegyük fel, hogy a súlypont a doboz (azaz. O) egyenlő a hidrosztatikus nyomás, a koordinátáit e pont ,. A mozgás sebessége ezen a ponton. Összetevői a sebesség végig a koordináta-tengelyek egyenlő ,.

Keresztül m. A vízszintes vonal, párhuzamos tengely. A metszéspontok az arcát a rovatban (arc 1234), A (arc 5678). Nyomás ezeken a pontokon, és a tengely mentén.

A folyékony folytonos közeg nyomást azon a ponton van kifejezve folyamatos koordináták függvényeként a folyamatos helyét a térben. Hidrosztatikus nyomás lineárisan változik a folyamatos, és a nyomás növekmény egy egységnyi hosszúságú - - -

Következésképpen a nyomás A és B pontok különböznek nagyságú.

A nyomás és B pontok expresszálható a következő formában:

Mivel a kis területeken a arcok lehet tekinteni, hogy a nyomás, és az átlagos hidrosztatikus nyomást az arcok 1234, és 5678. Felületi nyomás erőt a következő arcokat tengelyirányban nyomás megegyezik a termék a tér arcok:

Hasonlóképpen, a felületi nyomás erő szélén a Z tengely körül (arcok 1478i 2365):