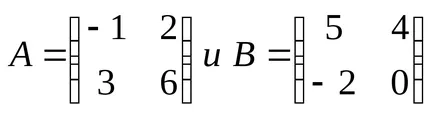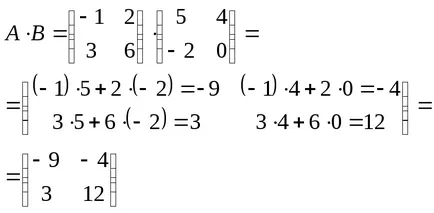Kiszámítása a determinánst gauss
Kiszámítjuk a meghatározója a Gauss módszer.
A módszer abban áll, a következő: a meghatározó csökkenti, hogy háromszög alakban segítségével elemi transzformációk, és ha egyenlő a terméket az elemek a fő diagonális.
ötlet módszer a következő: adott egy meghatározója a harmadik rend
elem
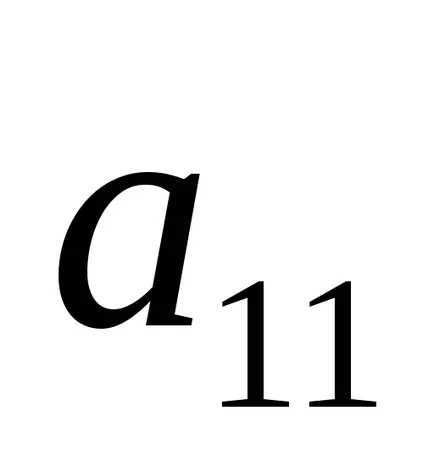
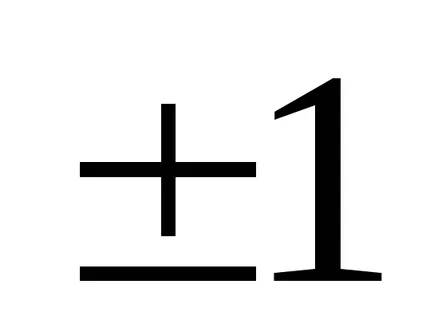
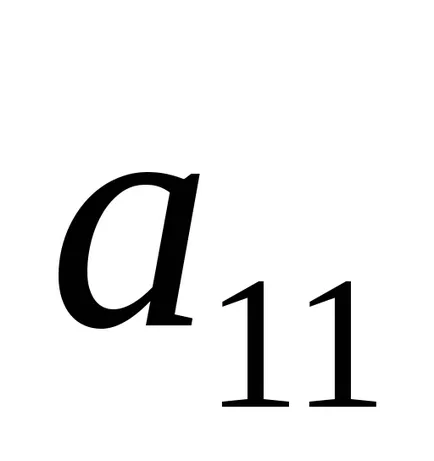
Megkapjuk a meghatározója a forma

Nullázni elemek állva az első oszlopban az első kivételével. Ehhez első vonjuk ki a második sorban szorozva
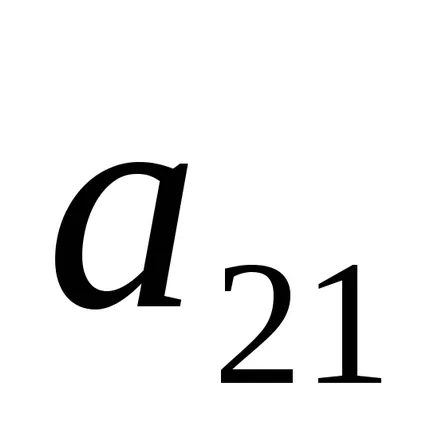

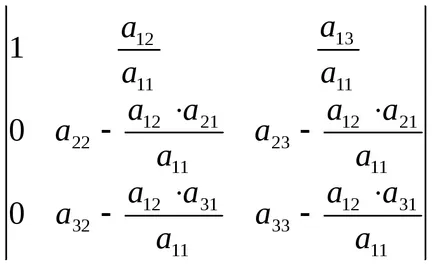
Jelöljük elemei betű c, akkor
Most meg kell állítani elem

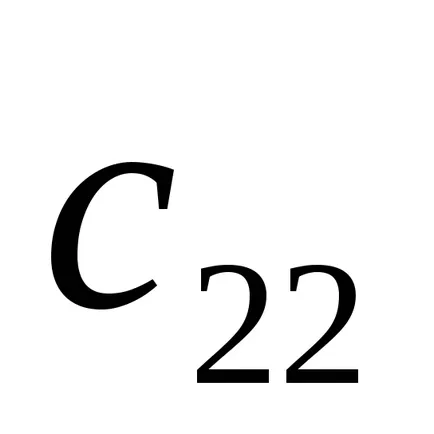
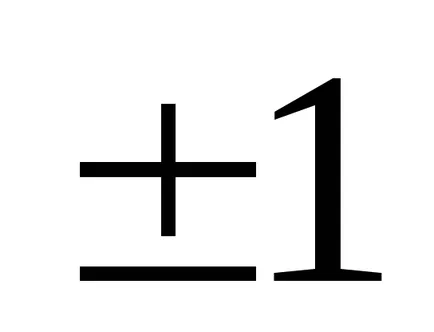
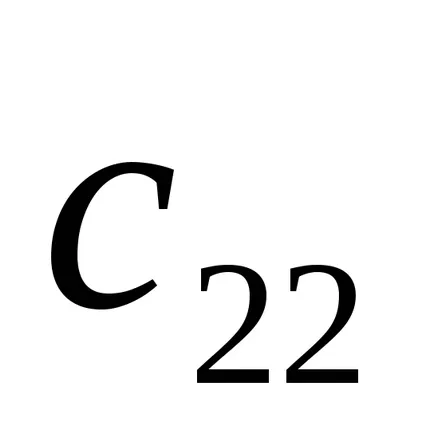
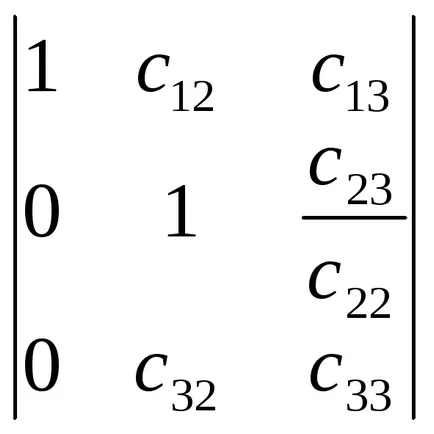
Ezután egy harmadik sor vonjuk ki a második szorozva

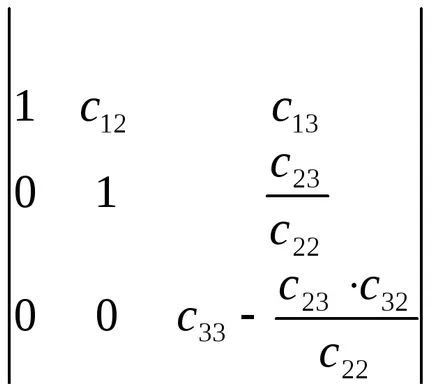
Jelöljük elemei a T betű, akkor
Itt vagyunk vezetett a meghatározója egy háromszög alakú, most már
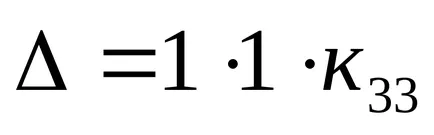
Vizsgáljuk meg most ezt a konkrét példát.
4. példa: Számítsuk determináns
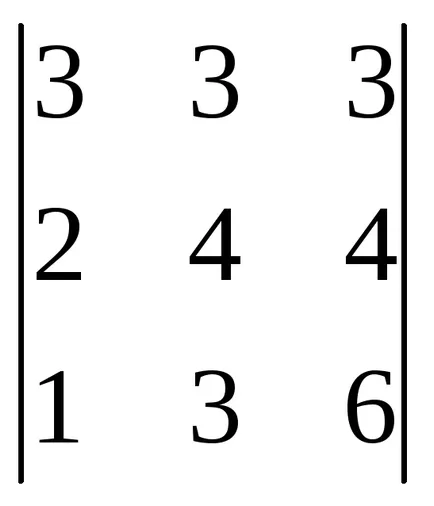
Megoldás: csere az első és a harmadik sorban (a csere két oszlop (sor) meghatározó változások ellentétes előjellel).
kivonjuk az első a második sorban, szorozva 2, majd vonjuk egy harmadik sorban első szorozni 3. Got

Ezután egy harmadik sor vonjuk ki a második szorozva 3.
§2.Matritsy mátrixok típusai
Definíció 7: Ha matritsemstrok instolbtsov, akkor nazyvaetsyarazmernostyu m

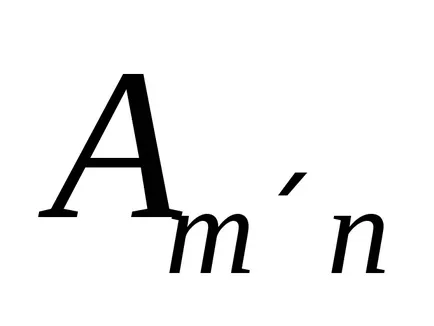
Definíció 8: Amennyiben
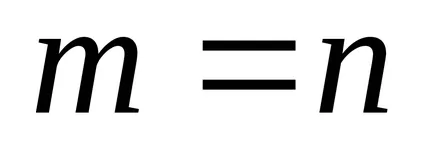
Definíció 9: álló mátrixot csak egy sor (oszlop) nevezzük a mátrix-sor (oszlop).
10 Meghatározás: A mátrix áll nullák, a mátrix az úgynevezett nulla.
Definíció 11: diagonális mátrix egy négyzetes mátrix, amelyben minden elem, amely nem tartozik a fő átló nulla.
Definíció 12: az identitás mátrix az úgynevezett diagonális mátrix, amelyben az összes elem a fő diagonális egyenlő eggyel.
Definíció 13: háromszögletű nevezett négyzetes mátrix, amelynek elemei vannak elhelyezve az egyik oldalon a fő diagonális nullával egyenlő.
Deystviyanad mátrixok.
Definíció 14: Két mátrix megegyezik, ha azonos számú sort és oszlopot, és megegyezik a megfelelő elemek.
A mátrixok A és B egyenlő legyen, azaz,
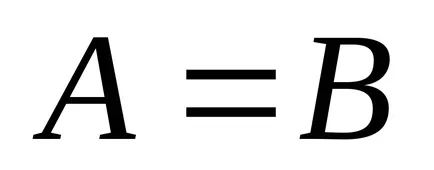
15 Definíció: Az összeget (a különbség) a mátrixok A és B jelentése C mátrix, amelyben minden elem megegyezik
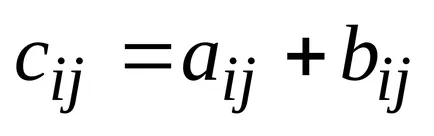
6. példa: Find a mátrix
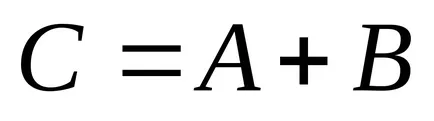
Tulajdonságok hozzáadás
0 2 A + D = A, ahol a D-nullmátrix
3 0 A + (B + C) = (A + B) + C (elosztó)
4 0 A + (- A) = O, ahol - szemben a mátrix
(Azaz, az elemek ellenkező előjelű)
16: A termék az A mátrix a számok
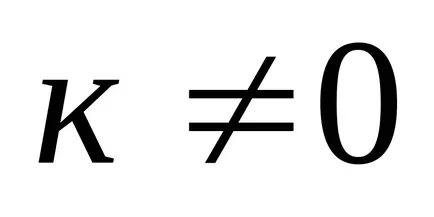

szorzás Matica
Ez az intézkedés vonatkozik az úgynevezett harmonizált mátrixban.
17 Meghatározás: A mátrix A koherens a B mátrix, ha az oszlopok száma a mátrix megegyezik a sorok számát a mátrix V.
8. példa:
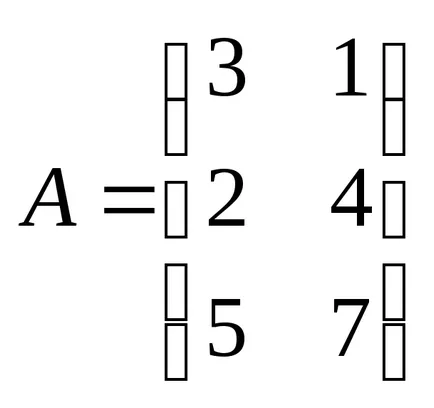
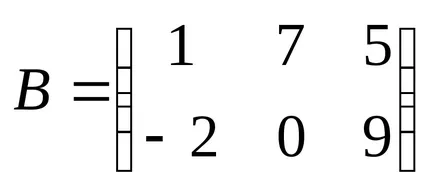
18 Meghatározás: A termék a két A és B mátrix egy mátrix C, ahol minden egyes elem összegével egyenlő termékek elementovistroki mátrix megfelelő elementyj-edik oszlopa mátrix V.
Ha az A mátrix méretükben
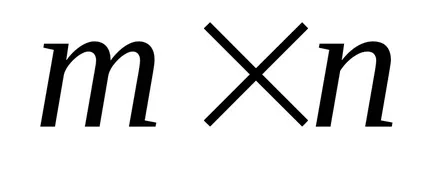
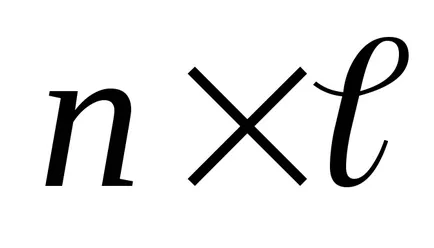
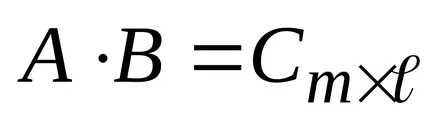
9. példa: Szorzás mátrix