Kommunikáció integráció differenciálás
Tekintsük a határozott integrál, amelynek alsó határa konstans és a felső megváltozott.
Amely a felső határa a különböző értékeket, akkor megkapjuk különböző értékeket az integrál; Következésképpen, ilyen körülmények között a integráljának függvényében annak felső határa
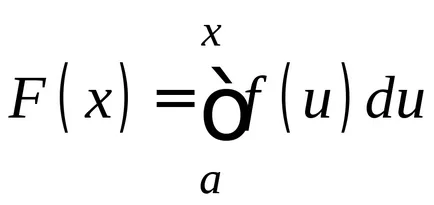
itt

Tétel 1.Proizvodnaya a szerves annak felső határa egyenlő a integrandust
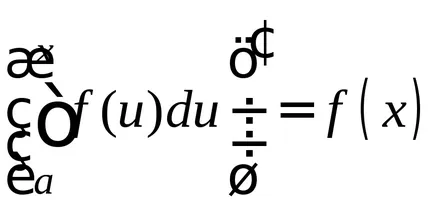
Tekintsünk egy folytonos részesülő nemnegatív értéket az intervallum
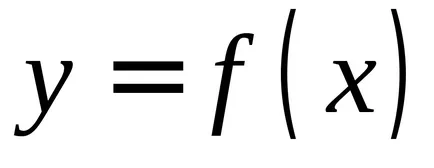

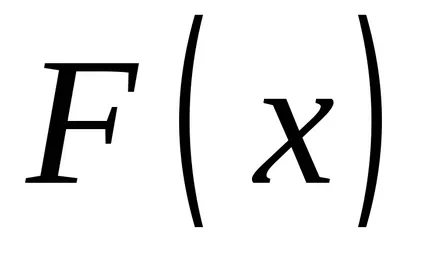
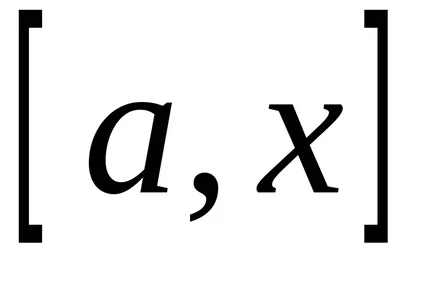
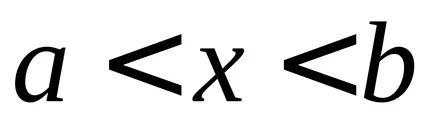
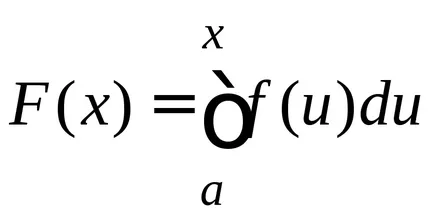
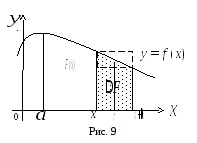
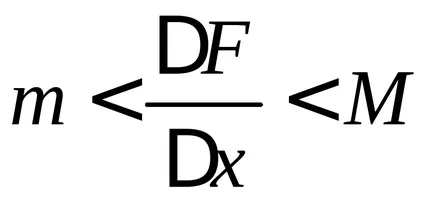
Ha a változó
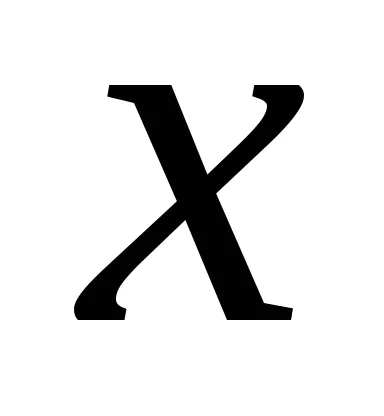

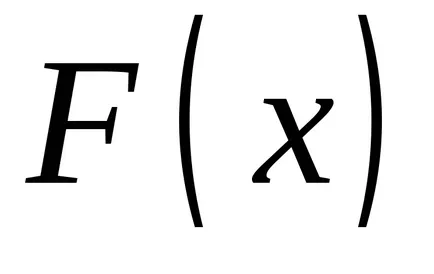

,
ahol
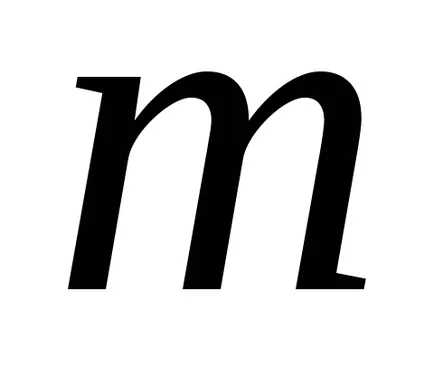
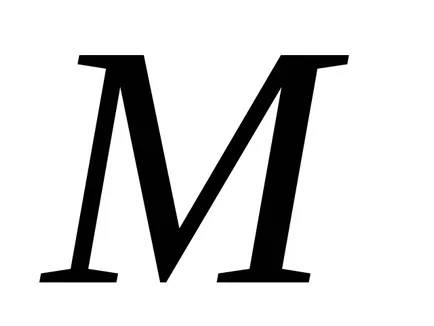
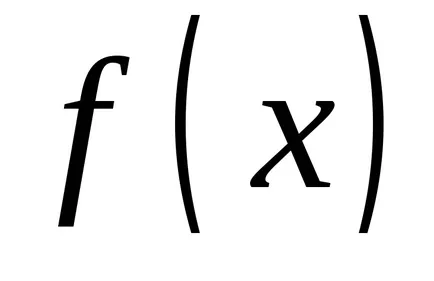
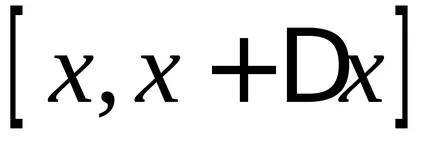


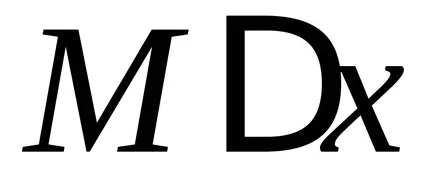

mert
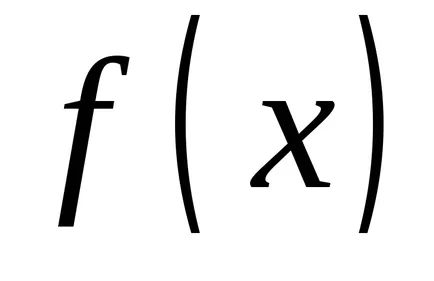
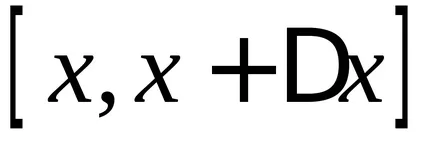
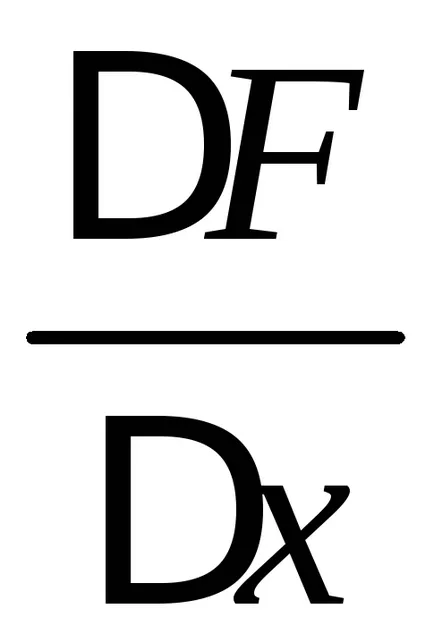
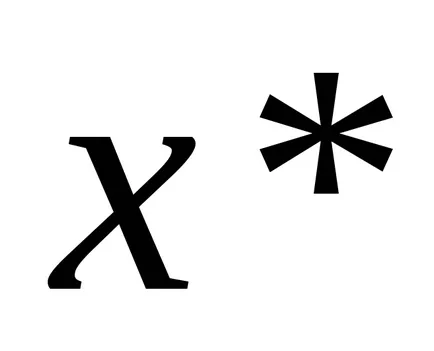
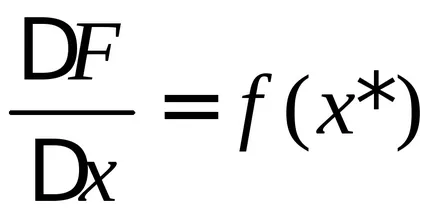
Tekintsük a határ ez a kifejezés, azzal a megkötéssel, hogy


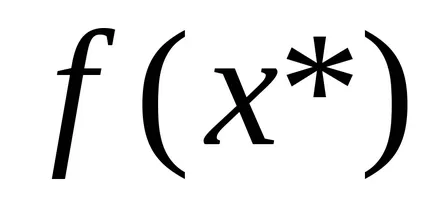
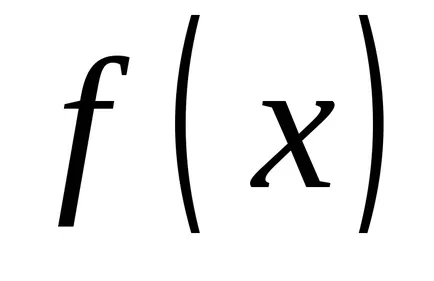
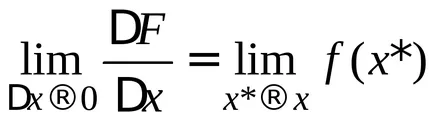
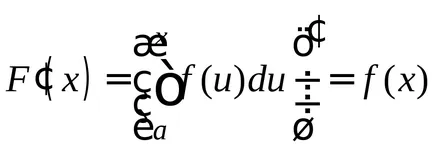
Megjegyzés: Ez a tétel azt mutatja, hogy az integráció és a differenciálás - az inverz műveleteket.
A határozatlan integrál
OPREDELENIE.FunktsiyuF (x), amely a származék az integrandus függvény úgynevezett primitív.
Hogyan lehet megtalálni a származékos volt az egyik fő feladata a differenciálszámítás, így arra a primitív ez az egyik fő célkitűzése az integrálszámítás.
Vegyük például a függvény
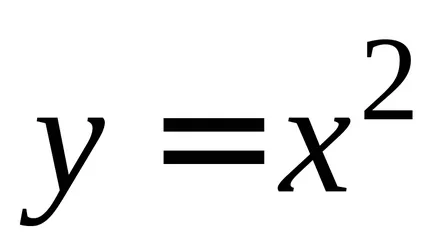
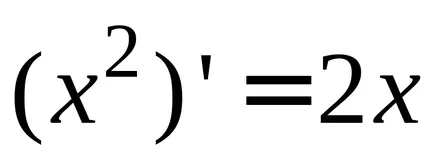
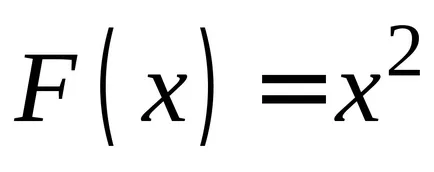
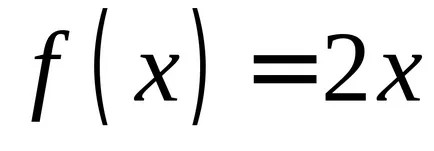
Ha úgy találja, a származékok funkciók
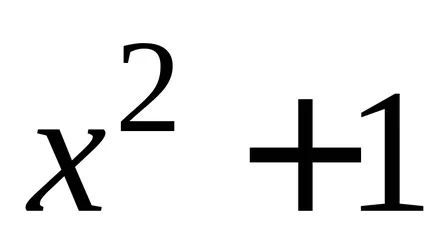
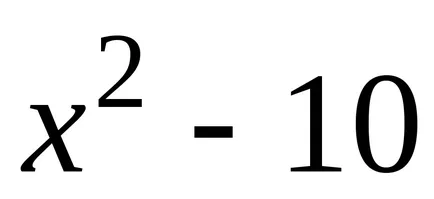
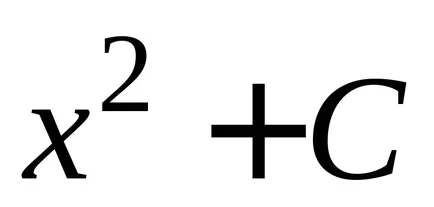

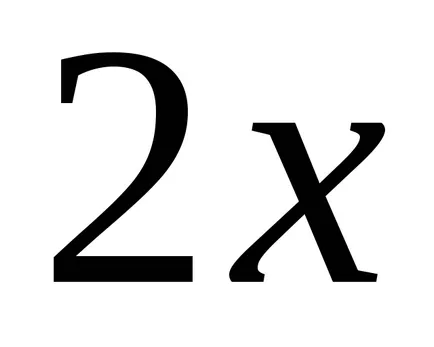
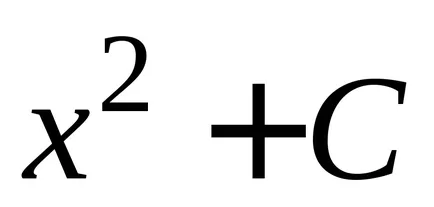
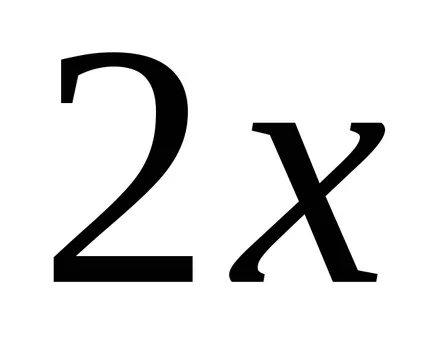
2. tétel minden folytonos függvény végtelen számú primitívek, és bármely kettő eltér egymástól csak konstans kifejezést.
Tegyük fel, hogy a függvény
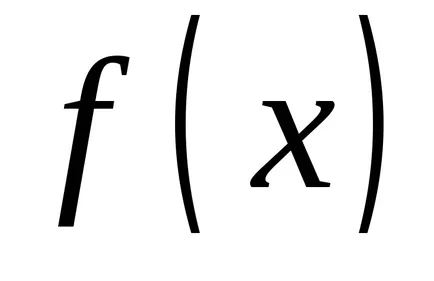
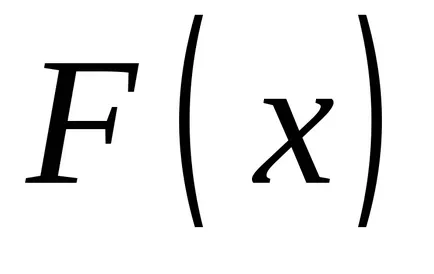
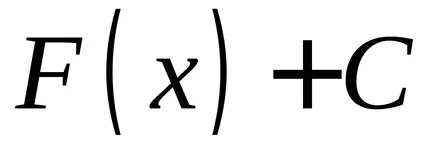

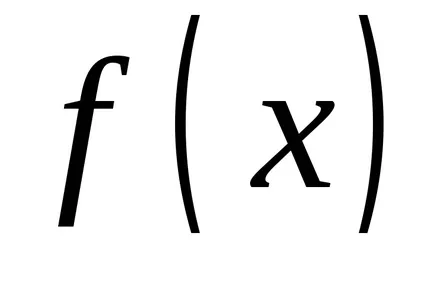
Let funkció
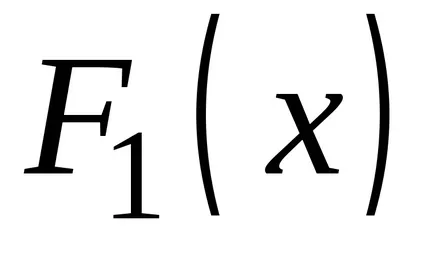
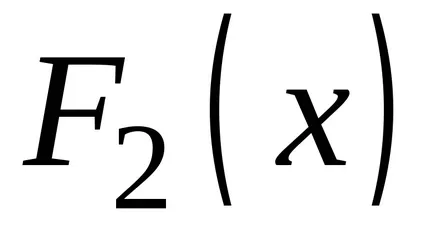
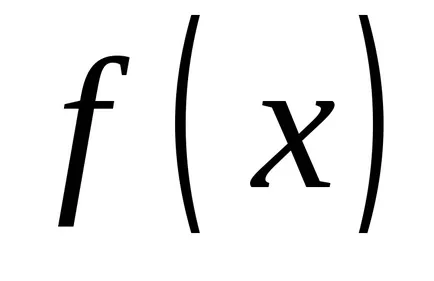
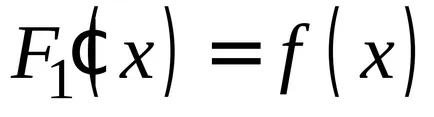
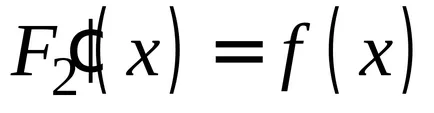
OPREDELENIE.Sovokupnost minden primitívek a integrandusz nevezzük határozatlan integrál.
A határozatlan integrál is nevezik specifikus, csak a határok nélküli, azaz ha
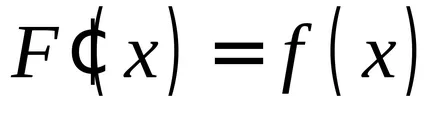
.
és

,
,
.
Menetrend primitív függvény
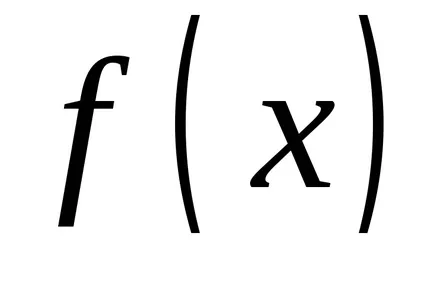
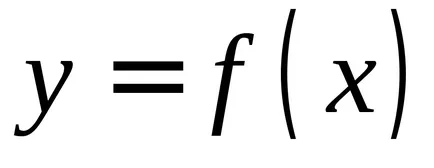
A meghatározása a határozatlan integrál, mint a több primitívek
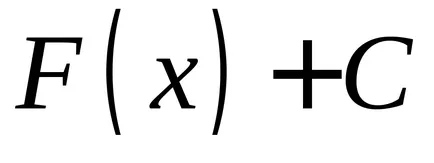
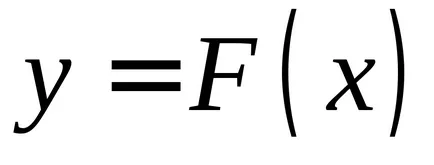

Az 1. táblázat mutatja a származékok és az alapvető primitívek elemi funkciók.