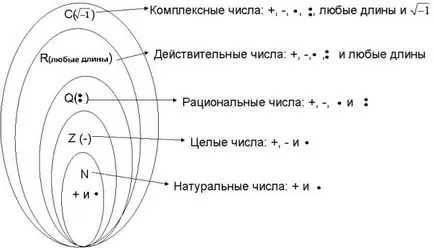
komplex számok

Komplex számok. Komplex az a szám, a forma z = a + biabRi2 = -1

Megjegyzés.
A tényleges száma a - a valós része a Z és jelöli a = Rez
A tényleges száma b - a képzetes részét Z és jelöljük b = lmz
A valós számok egy sor számok és műveletek őket, ami úgy tűnik, hogy ahhoz, hogy megoldja az összes feladatot a matematika. De hogyan lehet megoldani ezt az egyenletet a valós számok x2 + 1 = 0? Van még egy mellék szám - komplex számok. A komplex számok lehet venni a gyökerek a negatív számok.

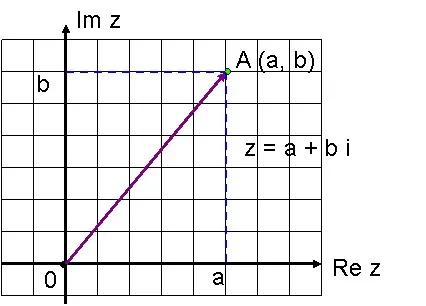
Algebrai alak a komplex szám. Algebrai formájában komplex szám van Vidz = a + bi (aRbRi2 = -1)

Megjegyzés. Ha a = Rez = 0b = lmz = 0, akkor Z jelentése nevezzük képzetes számot. Ha a = Rez = 0b = lmz = 0, akkor a hívott szám tisztán képzetes z

Geometriai értelmezése a valós számok egy igazi vonalat. Ezen túlmenően, a számegyenesen „nincs helye az új pontok”, azaz minden pont a valós tengelyen megfelel egy valós szám. Következésképpen a komplex számok ezen a vonalon nem lehet elhelyezni, de megpróbálhatod, hogy fontolja meg, valamint a valós tengelyt, amelyen fogjuk halasztani a valós része egy komplex szám, még egy tengely merőleges rá; hívjuk a képzetes tengelynek. Ezután minden z = a + ib komplex szám tudunk levelezésben a pont a koordináta síkon. A vízszintes tengelyen mi a telek valós része a komplex szám, és a függőleges tengely - egy képzeletbeli része. Ez létrehozza az egy-egy levelezés között a komplex számok, és minden pont a síkon. Ha ez a vonal épült, a koordinátasík úgynevezett komplex síkon. Értelmezése a komplex szám z = a + b i egy olyan vektor, OA koordinátái (a, b) kezdve az O pont (0,0), és befejezve pontnál (a, b)

A konjugátumok. Száma Z = a + bi, és z = a-bi konjugált komplex számok

Az ingatlan. Az összeg és a termék két komplex konjugált szám valós számok: z + z = 2azz = a2 + b2

Ellentett. Száma Z = a + bi és -z = -A-bi ellenkező komplex hívott számot.

Az ingatlan. Az összeg két ellentétes komplex számok nulla:
Z + (- Z) = 0

Egyenlő számban. Két komplex számok azt mondják, hogy egyenlő, ha azok a valós és képzetes része.

Hozzászólások komplex számok, adott algebrai formában:

tulajdonsága továbbá: összege két komplex szám Z1 = a + bi és Z2 = c + di van a komplex szám az űrlap Z = Z1 + z2 = a + bi + c + di = a + c + (b + d) i
Példa: 5 + 3i + 3i = 8 + 2i

kivonó Tulajdonság: A különbség a két komplex szám Z1 = a + bi és Z2 = c + di van a komplex szám az űrlap z = z1-z2 = a + bi-c + di = a-c + (b-d) i

megszorozzuk Tulajdonság: A termék két komplex szám Z1 = a + bi és Z2 = c + di van a komplex szám az űrlap z = z1z2 = a + BIC + di = AC-bd + (ad + bc) i

elosztjuk Property Self két komplex szám z1 = a + bi és z2 = c + di van a komplex szám vidaz = z2z1 = c + dia + bi = c2 + d2ac + bd + c2 + d2bc-adi

Hozzászólások komplex számok megadott trigonometrikus formában

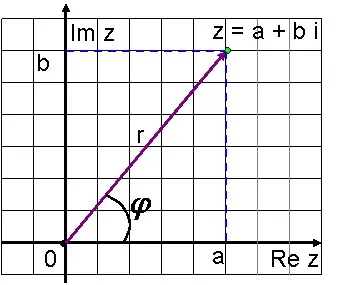
Rögzítése egy komplex szám z = a + bi formájában z = rcos + ISIN nevezett trigonometrikus forma egy komplex szám.

Modul komplex szám: r = a2 + b2

Az érv egy komplex szám: cos = műgyanta = rb

Képzeletbeli és a komplex számok

Tekintsük hiányos másodfokú egyenlet:
x 2 = a,
ahol egy - egy ismert mennyiségű. A megoldás az egyenlet felírható:
Három lehetőség van:

1). A = 0. Ha x = 0, akkor.

ahol a, b - valós szám, i - imaginárius egység.

Példa Példa komplex számok s 3 + 4 i. 7-13,6 i. 0 + 25 25 i = i. 2 + i.

Ismerkedés a képzeletbeli és a komplex számok, lásd „imaginárius és komplex számok.” Szükség van egy új típusú számok jelentek meg Másodfokú egyenletek megoldása esetén a D
Beszorozva számláló és a nevező 2 + 3i

kezdve az összes változás, megkapjuk:
Geometriai ábrázolása komplex számok. A valós számok képviselik pont a számegyenesen: ahol számát jelöli 3. pont B pont - a 2 és O - nulla. Ezzel szemben a komplex számok képviselik pontokat a koordináta síkon. Mi választjuk ki ezt a téglalap (derékszögű) koordináták azonos méretű mindkét tengelyen. Ezután a komplex szám egy + bibudet képviseli P pont a abszcissza a és ordináta b (lásd. Ábra.). Ez koordinátarendszer úgynevezett komplex síkon.

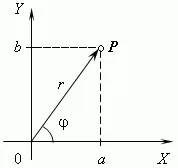
A modulus komplex szám a vektor hosszának OP, ábrázol egy komplex számot a koordináta (komplex) síkon. komplex szám a + bi modul kijelölt | a + bi | vagy írni, és r egyenlő:
Konjugált komplex számok azonos modult. __

Az érv egy komplex szám - az a szög között OX tengelye és a vektor OP, ábrázol egy komplex szám. Ennélfogva, tan = b / a.

Trigonometrikus forma egy komplex szám. Abszcissza a és ordináta b komplex szám a + bi fejezhető ki a modulusa R, és egy érv.
Műveletek komplex számok képviselik a trigonometrikus formában.

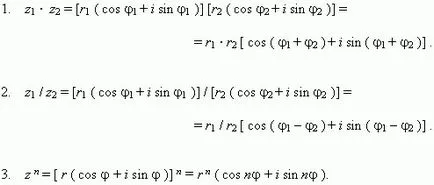
Ezt a formulát Moivre.
Itt k - egységet. Annak érdekében, hogy különböző értékeket gyökér n n-edik hatványa Z szükséges adja meg értékeket az n egymást követő k (például K = 0, 1, 2, ..., n - 1).