Központ párhuzamos erők - előadások és példák megoldások teormeh feladatok szilárdságtani, műszaki és
Képzeljünk el egy rendszert a párhuzamos erők 1. F2. Fn>. Elfordításával az összes rendszer erők egy és ugyanazon szög a hatóirányának az eredő erő párhuzamos rendszer viszont az azonos irányban azonos szögben a körül a pont (1.5 ábra, a).
Ez a pont az úgynevezett központja párhuzamos erők.
Szerint Pierre Varignon tétel. ha a rendszer rendelkezik az eredő erő, a pillanat bármilyen központ (tengely) az összege a pillanatokban a rendszer erői viszonyítva ugyanolyan középpontja (tengelye).
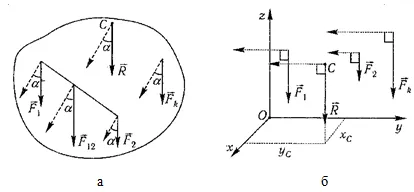
Annak megállapításához, a középpontjának koordinátáit párhuzamos erők használják ezt a tételt.
Relatív, hogy az x-tengelyen
az y
Annak megállapításához, a koordináta-ZC. minden erő forgatni 90 ° -kal úgy, hogy azok párhuzamosak az y tengelyhez (1.5 ábra, b). majd
Ezért, a képlet meghatározására sugár középpontjához vektor válik párhuzamos erők
Tulajdonságai központjában párhuzamos erők:
- Összege a pillanatok az erők Fk képest a C pont nullával egyenlő ΣMC (Fk) = 0.
- Ha minden bekapcsolást egy bizonyos szögben α. megváltoztatása nélkül pontok az erő alkalmazása, a közepén egy új rendszer párhuzamos erők ugyanazon a ponton C.