Lecke „mozgalom
Rövid leírása a dokumentum:
Szöveg kódolása tanulság:
Mi továbbra is tanulmányozza a mozgást.
A legutóbbi leckében megismerkedtem egy fajta mozgás - tükörszimmetriával.
Emlékezzünk, hogy tükörszimmetrikusan egy térkép saját magára, amelyben minden egyes pontban K válik szimmetrikus síkban β s pont K1.
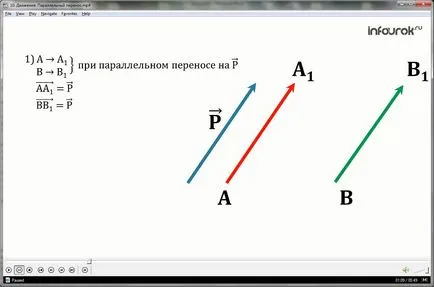
Feltérképezése saját magára, miáltal bármely ponton M megy egy pont M1, MM1, hogy a vektor p vektor -nazyvaetsya párhuzamos fordítást a vektor által p.
1. A definíció szerint a párhuzamos átvitel a p vektor, bármely két pont, A és B vált a ponton az A1 és a B1, úgy, hogy a vektor p vektor AA1 és a BB1 vektor vektor p.
2. szabály a háromszög van:
3.Priravnyaem jobb oldali egyenletek:
Mivel a vektor AA1 és BB1 - ez egy p vektor, megkapjuk:
= 1. így elérjük, hogy a pontok közötti távolság az A és A1, B és B1 van tárolva, akkor a párhuzamos transzlációs vektor által p mozgását.
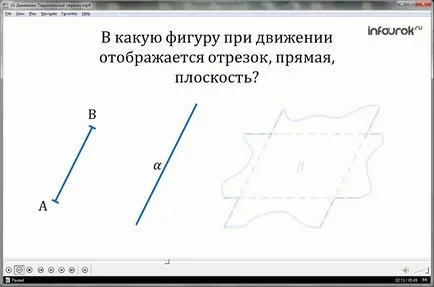
Melyik ábra egy olyan szegmenst, a mozgás, vonal, sík? (Szünet)
Amikor a mozgó egy szegmens mozog a szegmens, egyenes - egyenes vonalban, egy síkban - a síkban.
Bármilyen bevezetését, amellyel bizonyítjuk, hogy a számok, mint a mozgás.
Alkalmazzuk ezt a tudást, hogy megoldja a problémákat.
Triangle A1V1S1 kapott párhuzamos fordítását ABC háromszög a vektor által p. Pontok M és M1 - illetve, a metszéspont a medián az ABC és A1V1S1 háromszögek. Igazoljuk, hogy a párhuzamos átviteli vektor által p válik az M pont az a pont M1.
1. Mozgás - ez a leképezés magára, amely megőrzi a két pont közötti távolság. Párhuzamos közlekedés mozgás, akkor AB = A1B1, BC = B1C1, A1C1 AC =.
Háromszögek ABC és A1V1S1 megegyezik a harmadik egyenlősége alapján háromszögek.
2.Dopolnitelnoe konstrukció: töltik a szegmens AM és A1M1. Azt is kerül (sor egyenlő háromszögek).
3. Egy lapos négyszög AMM1A1 van: AM║ A1M1 és A1M1 AM =
4.Takim módon, alapján a paralelogramma AMM1A1 - paralelogramma vektort a vektor MM1 AA1 egyenlő a vektor p.

Bebizonyítottuk, hogy a párhuzamos fordítás a p vektor M pont a lényeg az M1.
QED.
Mi az a pont kell építeni MN híd a folyón, amely elválasztja a két falu adatokat az A és a B úton AMNV faluról falura A B volt a legrövidebb? (River bankok tartják párhuzamos vonal, a híd épül merőleges a folyó).
1.Predpolozhim, hogy bizonyos rendelkezések talált a hídon.
Ezzel párhuzamosan elmozdulás figyelembe az M pont-pont N, A pont fog mozogni egy pont A1.

2. Ezután az AM + NB = MN + AA 1 + + A1N NB AA1 + A1B (három pont nem illeszkedik egy egyenes vonalat kell végezni háromszög-egyenlőtlenség - az összeget a két fél több mint egyharmada), valamint az egyenlő érhető el, ha az a pont A1, N és B hazugság egy sorban.
3.Otsyuda eljárás magában foglalja az alábbi konstrukciót: elvégzésére párhuzamos átviteli pont a vektor. Az A pont mozog egy pont A1.
A kapcsolódási pont A1 a B pont, megkapjuk a D pont, amely a kiindulási pont a híd.