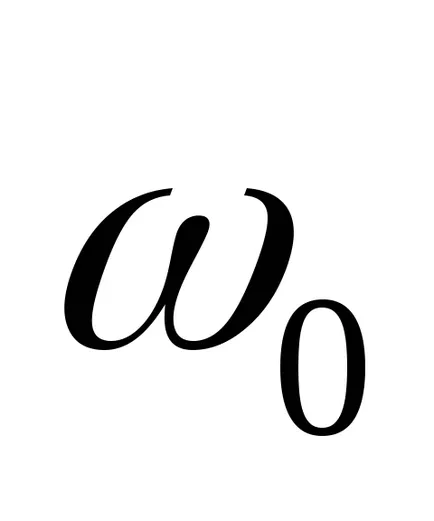Lengyelek és nullák

Sok a dinamikus rendszer tulajdonságai (pl, sebesség, túllövés) határozza meg a pólusok az átviteli függvény (vagy ezzel ekvivalens, a sajátértékei mátrix

modell az állam térben).

Az átviteli függvény felírható a termék a átviteli függvények elemi egységet az első és másodrendű. Így több pólust az átviteli függvény egy stabil rendszert képeznek pólus átviteli függvények a két típusú elemi egységek: aperiodikus és oszcillációs.

Aperiodikus kapcsolatot az átviteli függvénnyel

Ez egy egyedi jellemzője - az időállandó. Körülbelül 5 frekvencia , Frekvenciaátvitel a link csökkenni kezd, a nullához közelít.

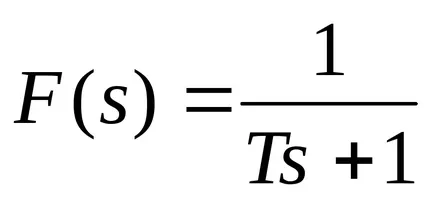
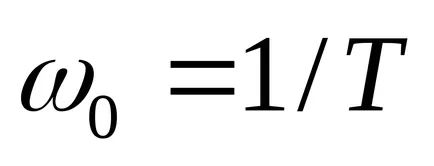
Az oszcilláló egység rendelkezik egy átviteli függvény

, ahol- időállandó és. frekvencianazyvaetsyasobstvennoy frekvencia (naturalfrequency), a paraméterParaméterek csillapítás csillapító ilikoeffitsientom (dampingfactor). A csökkenéspulzus és átmeneti funkciók válnak kifejezettebbé oszcillációs jellegű, és úgy tűnik, az AFC „púp” a terület frekvencia. A határesetbencsillapítatlan rezgések, és a link nazyvaetsyakonservativnym. Másrészt, havalódi gyökere a nevező, és az egység lesz aperiodikus eleme a másodrendű.

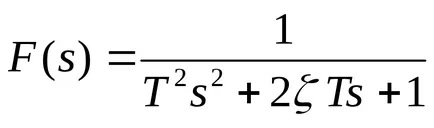
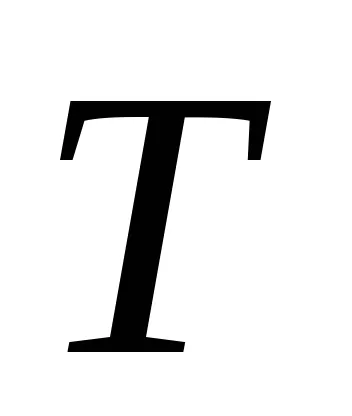
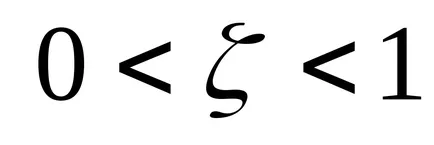
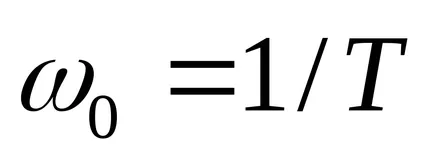
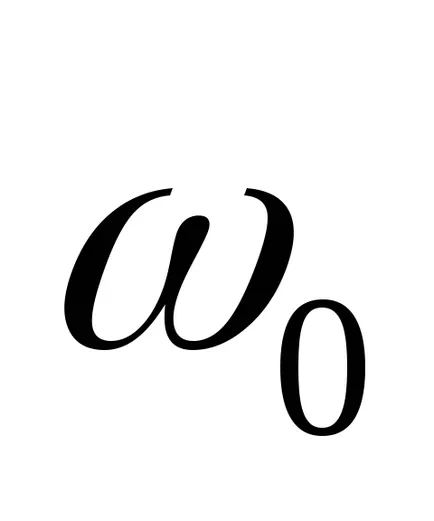
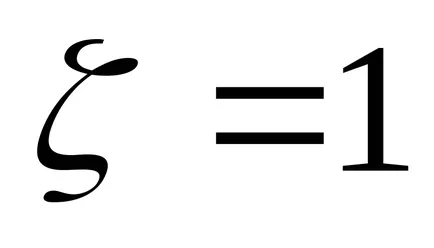
Ahhoz, hogy megtalálja a pólusok az átviteli függvény f használhatja a

>> [w0, zéta, p] = nyirkos (f)

Ez lehetővé teszi, hogy megtalálja a nem csak a pole p. hanem a megfelelő saját chastotyw0 és tényezők dempfirovaniyazeta tömbként.

A nullák az átviteli függvény f számítjuk

A rendszer stabilitásának nem függ a helyét a nullákat, de jelentősen befolyásolják az átmenet folyamatában. csapat

az épület egy térképet helyét nullák (amely jelzi körök) és a lengyelek (keresztek) rendszerek a komplex síkban.

1Chernym szín jelzi a felhasználó által megadott, a kék - sredyMatlab választ.

2B külföldi szakirodalomban egydimenziós rendszerekben használt sokraschenieSISO = SingleInputSingleOutput.

3Polyusa átviteli függvény sajátértékei mátrix

. Így, ha az átviteli függvény pólus pontnál, mátrixEz degenerált.

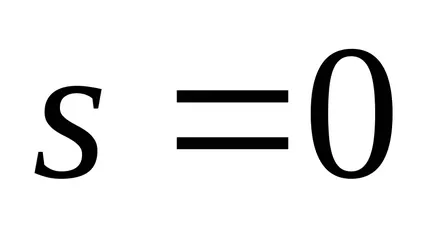
4A nemlineáris rendszerek nem igaz.

5Znachenie

funktsieydamp visszatér a természetes frekvencia az igazi pole.