Lineáris harmonikus oszcillátor kvantummechanikai
Lineáris harmonikus oszcillátor -
teljesítő rendszerben egy egydimenziós mozgás feszültségű alatt quasielastic B-ly - a használt modell sok problémát a klasszikus és a kvantumelmélet (lásd §142.). Tavaszi egyének ég és a matematikai inga - a méretre klasszikus harmonikus Oszcilloszkópok szigetelők.
A potenciális energiája a harmonikus oszcillátor, a második (lásd. (141,5)) a
ahol W0 - sajátfrekvencia oszcillátor, m - részecske tömege. Tengely-függőség (222,1) formájában van a parabola (ris.300), azaz „Lehetséges jól” ebben az esetben parabola. Kis amplitúdójú rezgések osztályú oszcillátor, határozza meg a teljes energiafelhasználás E (lásd. Ábra. 16). A point-esek koordinátákkal ± xmax teljes Ener-lógia E egyenlő a potenciális energia. Ebben, a klasszikus szempontból rész-ca nem léphet túl a pályát (-hmax. + Xmax). Az ilyen visszavonás azt jelentené, hogy a potenciális energia nagyobb, mint a fele távon, ami abszurd, hiszen ez vezet téged, a víz, a kinetikus energia negatív-nek. Így a klasszikus egy-tsillyator egy „potenciális
pit „koordinátákkal -xmax £ x £ xmax
„Anélkül, hogy kijuss” belőle.

A harmonikus oszcillátor kvantummechanikai-üvöltés - egy kvantum oszcillátor -
Schrödinger-egyenlet írja le (217,5), figyelembe véve a kifejezést (222,1) a potenciális energia. Tor-állami és stacionárius kvantum oszcillátor határozza meg a Schrödinger egyenlete formájában
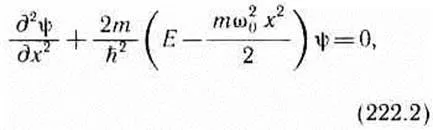
ahol E - teljes energia az oszcillátor. Az elmélet differenciálegyenletek bizonyítást nyer, hogy az egyenlet (222,2) újra gyűrődések csak a saját energiáit
Képlet (222,3) azt mutatja, hogy az energia egy kvantum oszcillátor lehet csak diszkrét értékeket, azaz. E. kvantálja Xia. Energia korlátos alábbiakban nem nulla, mint egy négyszögletes „lyuk” a végtelenül magas „falak” (lásd. §220), a minimális érték Ener-ology E0 = 1/2 hw0. Létezik egy minimális távú energia - ez az úgynevezett nullpont energia - jellemző kvantum rendszerek és társ-mérkőzés közvetlen következménye nedves típusú bú-ratio-meghatározás.
A jelenléte nulla oszcilláció azt jelenti, hogy a részecske nem lehet az alján a „potenciál jól”, és ezt a következtetést független annak alakját. Tény, „drop hogy az alján a jól” van társítva a húzott-niem nulla lendület a részecske és ugyanabban az időben és bizonytalansága. Ezután a nem meghatározására koordináták válik tetszőlegesen nagy, ami ellentmond viszont a részecskék maradnak a „potenciális jól”.
Arra a következtetésre jut, hogy van-e áram nullára-oszcilláció egy kvantum oszcillátor anti-rechit következtetéseit a klasszikus elmélet, amely szerint a CO-legalacsonyabb energiájú, Koto-Rui lehet egy oszcillátor nullával egyenlő (megfelelő pihenni az egyensúlyi helyzet a részecske). Például a klasszikus fizika ság arra a következtetésre vezet, hogy a
T = 0, az energia a rezgőmozgás atomok egy kristály kell tűnnie. Következésképpen meg kell tűnnie, és a fényszóró miatt vibrációs-niyami tartalmaz. Azonban, amíg a kísérlet azt mutatja, hogy a fényszórás-intenzitás csökken, ha a hőmérséklet nem jól lu, és hajlamos arra, hogy egy határértéket, jelezve, hogy a T -> 0 atomi rezgések a kristály nem törik. Ez validált nulla niem oszcillációk.
Képlet (222,3) az is következik, hogy az energia szintjét a lineáris harmonikus oszcillátor vannak elrendezve egyenlő távolságra egymástól (ris.300), nevezetesen, a távolság a szomszédos energiaszintet egyenlő hw0. ahol a minimális energia értéke
A szigorú problémájának megoldása kvantum oszcillátor vezet újabb zna jelentősen eltér a klasszikus versenyt figyeli. Kvantummechanikai számítások azt mutatják, hogy a részecske lehet érzékelés-kívül élni a megengedett területen | x | £ xmax (lásd a 16. ábrát ..) mivel a klasszikus szempontból, akkor nem megy túl a szántóföldön (-hmax, + x: max). Így, van egy nem nulla valószínűsége, hogy a részecske a régióban, amely klasszikusan tilos. Ez az eredmény (anélkül, hogy a vízben) ábrán látható. 301, ahol annak a valószínűsége, sűrűsége a kvantum-Ness w oszcillátor kimutatására állapotának n = 1. Az ábra azt mutatja, hogy a kvantum oszcillátor Valóban
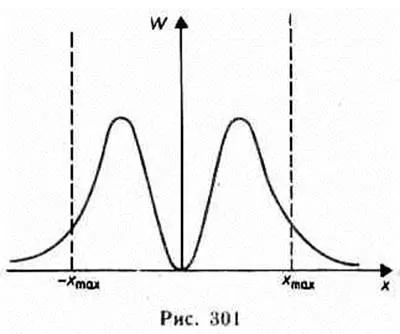
de a valószínűsége sűrűsége w véges-értékei kívül klasszikusan megengedett régió | x | £ xmax. t. e. rendelkezik Xia véges (de kicsi) valószínűsége, hogy egy részecske területén predela-
E „potenciális jól”. A létezése nem nulla értékek aw limit mi „potenciális jól” magyarázza cart-lehetőséget mikrorészecskék áthaladó potenciálfal (lásd. §221).
• Mik a fázis és csoport sebesség a foton?
• Ebben az esetben, miért és mikor Dvx / vx feltételek <<1 и Dvx /vx »1 можно говорить о движении частицы
egy bizonyos utat?
• Mivel az alapja a határozatlansági reláció, magyarázza a jelenléte a természetes szélessége spektrális vonalak?
• Mi a tér a hullám funkció? Miért kvantummechanika statisztikai elmélet? Mi a különbség a megértés az okság klasszikus és kvantummechanikai?
• Hogyan lesz a potenciális akadályt az átláthatóság tényező a növekedés a szélessége a felére?
• A Can részecske alján a „potenciális jól”? Vajon által meghatározott formában a „jól”?
• Mi a különbség a kvantummechanikai és a klasszikus leírását harmonikus oszcillátor-ra? A következtetések ezen leírások?
28.1. Szabad részecske mozog sebességgel. Bizonyítsuk be, hogy a kapcsolat
28.2. Az elektron mozog a hidrogénatom az első Bohr pályán. Feltételezve, hogy a megengedett-ráta bizonytalanság május 1% annak számérték, hogy meghatározzuk a koordinátákat az elektron bizonytalanság. Akár alkalmazható ebben az esetben a koncepció az elektron pályája? [Dx = 33 nm; no]
28.3. y-funkciója a részecske által adott y = (A / R) e -r / a, ahol r - távolság a részecske
Power Center, a - állandó. Határozza meg az átlagos távolság
28.4. Feljegyezzük a Schrödinger-egyenlet egy elektron stacionárius állapot található a hidrogénatom.
28.5. Elektron az egydimenziós téglalap „potenciális jól” végtelen L szélessége-Sure magas „falak”. Határozza meg a középső harmadában „gödör”, ha az elektron a gerjesztett állapotban elektron detektálás valószínűsége W (n = 2). EGYÉNI magyarázni-nek értelmében az eredményt grafikusan felismerés sűrűségfüggvénye az elektron egy adott állapotban. [W = 0,195]
28.6. Négyszögletes potenciálgát szélessége 0,1 nm. Határozza meg a elektron végrendeletek perces különbség energiák U-E, amelyekben a valószínűsége az elektron halad át a gáton lesz 0,99. [0,1 MeV]