lineáris programozási

x1. x2. xn - bemeneti változók, xn + 1. xn + 2. xn + m - további változókat. Minden további változókat vettük alapul. és kiindulási változók, mint nem-bázikus (további rögzített első oszlopában az asztal és a szimplex kiindulási az első sorban). Mindegyik ismétlésnél a szimplex táblázat elemei újratervezi bizonyos szabályok szerint.

Szimplex módszer algoritmus.

Itt látható a LP probléma kanonikus

Abban az esetben, ha az eredeti probléma kell találni legalább - a az együtthatók előjelei a célfüggvény F fordított a0, n = -a0, n. Jelek megszorítások koefficiensek „≥” megjelölés csak megfordult. Ha az állapot tartalmazza a jel „≤” - együtthatók vannak írva változatlan.

0. lépés alkotunk a szimplex tábla megfelelő eredeti probléma

1. lépés: Ellenőrzés valódiságát.

Ellenőrizze a pozitív elemei a B oszlop (konstans kifejezések), ha egyikük sem negatív, akkor azt találtuk, a lehetséges megoldást (oldat egyikének megfelelő a csúcsai a poliéder körülmények között), és mi folytassa a 2. lépéssel Ha vannak negatív elemeket az oszlopban a tagok, hogy válasszon közülük legfeljebb modul - ez határozza meg a vezető k húr. Ez a vonal megtalálható a maximális modulus negatív elem ak, l - ez határozza meg a vezető oszlop A - l és az egyik vezető tagja. Változó megfelelő a vezető sorban van zárva a alapján, a megfelelő változót tartalmazza a vezető oszlop alapján. Újraszámolja a szimplex tábla szabályai szerint.

Ha vannak negatív elemek, amelyek a szabad tagok - és a megfelelő sorban - nincs a feladat feltételei ellentmondásosak, és nincs megoldásokat.

Ha ezek után újratervezés szabad tagjai az oszlop maradt otritsaetelnye elemeket, akkor folytassa az első lépés, ha nincs, akkor a második.

2. lépés: Ellenőrizze optimalitást.

Az előző szakaszban találtunk egy lehetséges megoldást. Ellenőrizze, hogy az optimum Ha elemei között a szimplex tábla nahodschihsya sorban F (figyelmen kívül hagyva az elem b0 - az aktuális érték a célfüggvény) nem negatív, akkor megtaláltuk az optimális megoldást.

Ha az F sorban, vannak negatív elemei az oldat javítani kell. Közötti választás a negatív elemeket az F sorban a maximális modulus (kivéve az a függvény értékét B0)

l - egy oszlopon, melyben ő, hogy a vezető. Annak érdekében, hogy megtalálják a vezető vonal, meg az arány a megfelelő szabad tagja és vezető oszlop, feltéve, hogy azok nem negatív.

A K - sorok, amelyeknél ez az arány minimális - vezető. ak elem, L - Presenter (lehetővé teszi). Változó megfelelő a vezető sor (xk) ki van zárva alapján a változó megfelelő a vezető oszlop (xl) benne van az alapon.

Mi újraszámolja a szimplex tábla képleteket. Ha negatív elemek továbbra is az új kiosztási tábla után az F sorban folytassa a 2. lépéssel

Ha nem talál egy vezető vonal, mivel nincs pozitív elem a vezető oszlop területén megvalósítható megoldásokat a probléma a funkció nem kizárólag - az algoritmus leáll.

Ha a vonal F oszlopban tagjainak valamennyi elem pozitív, akkor azt találtuk, az optimális megoldást.

Transzformációs szabályokat simplex asztalra.

Kidolgozásakor az új szimplex tábla benne az alábbi változások történnek:

• Ehelyett az alapvető változó xk írási XL; ahelyett, hogy a nem-bázikus változók xl levelet xk.
• a meghajtó elem helyébe a reciproka ak, l „= 1 / ak, l
• minden elem vezető oszlopon (kivéve ak, l) szorozva -1 / ak, l
• minden elem vezető sorban (kivéve ak, l) szorozva 1 / ak, l
• fennmaradó elemeit szimplex táblázatban alakítjuk a képletű ai, J „= ai, j - ai, l x ak, J / ak, l

Reakcióvázlat konverziós elemeket simplex táblázat (kivéve a vezető sor és oszlop ólom) rendszer az úgynevezett „téglalap”.

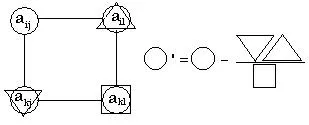
Átalakítható elem ai, J és a megfelelő három tényező csak a tetején a „négyszög”.