Másodrendű polinom közelítését, a számítást a átviteli koefficiensek - automatikus
A modell által leírt egy másodfokú egyenlet a következő formában:
Ahhoz, hogy megtalálja az együtthatók a, b, c, valamennyi feltétel teljesül az objektum alkotják a szabályozási rendszer a másodrendű algebrai egyenletek száma, egyenletek a rendszer állapotainak száma a tárgy a kísérlet:
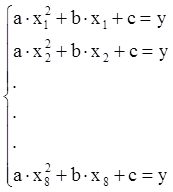
Hogy oldja meg a rendszer algebrai egyenletek használjuk a mátrix legkisebb négyzetek módszerével. A mátrix kialakításához a bemeneti és kimeneti jelek:
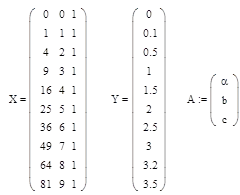
Kapunk egy rendszer három ismeretlennel: X. A = Y
Mi megoldjuk a mátrix egyenlet:
ahol A - mátrix a másodrendű polinom együtthatók.
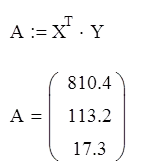
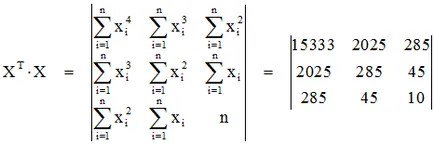
Mi olyan rendszert három algebrai egyenletek
Döntés, mi határozza meg az együtthatók a, b, c.
Mi található a fő meghatározója a rendszer:
Találunk a meghatározó kiegészítő rendszerek:
Keressük az együtthatók a, b, c:
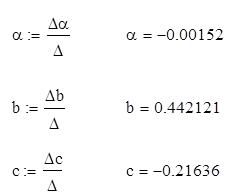
Így van másodrendű polinom:
y = -0,00152. xi 2 + 0,442121. xi -,21636
Kiszámításához az értékelést kapott értéket polinom függvények, és hasonlítsa össze őket a kísérleti adatokkal:
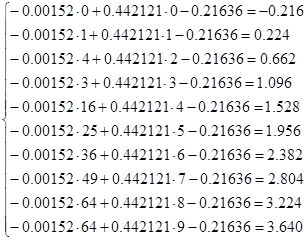
Az eredményeket a 3. táblázat foglalja össze
A négyzetösszege eltérések egyenlő: yi 2 = 0,173
A következő egy olyan számítás az ellenőrzés modell az objektum az elsőrendű egy számítógépes rendszer MathCad.

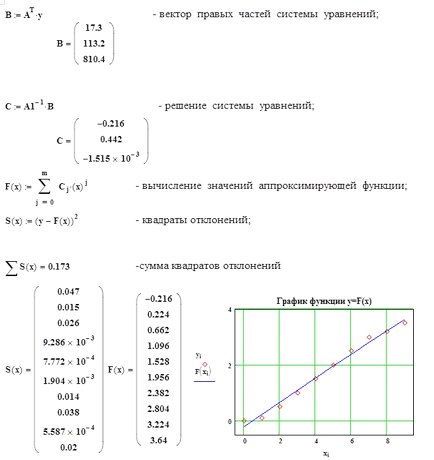
Összehasonlítva a eltérések négyzetösszegét azt mutatja, hogy a másodrendű polinom csak kissé pontosabban viselkedését írja le a tárgyat, mint az első polinomot. Amiből az következik, hogy a viselkedése egy tárgy engedelmeskedik az egyenlet nagyon közel egyenlet sorban. Számításokhoz egyenlet segítségével találtak a másodrendű polinom.
Kiszámítása átviteli együtthatók
A statikus modell az elsőrendű átviteli tényező meghatározása, mint a származék a kimeneti változó:
objektum együttható megmutatja, milyen irányba és milyen mértékben van jel változás, amikor áthalad egy tárgy, amely az erősítő egy objektum tulajdonságait.
A statikus modell az elsőrendű átviteli tényező meghatározása, mint a származék a kimeneti változó:
A statikus modell másodrendű együttható meghatározása a származékot a kimeneti változó:
Kiszámítása végrehajtott együtthatószám a továbbító 10, 50 és 90%
Mi az A értékét az átviteli együttható 10% az alábbi képlet szerint:
ahol - a maximális érték a folyamatos jelet.
- a minimális érték jel.
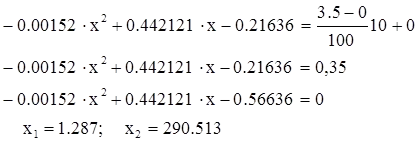
Behelyettesítve ezeket az adatokat, kapjuk:
Válassza x1, mert ha belép a tartományban a kísérleti értékek. Helyettesítő x1 értéke (1,2), és megszerezni az értéke a nyereség 10% névleges működés:
Számítsuk ki a értéke a nyereség 50%, amelyet a képlet:
Behelyettesítve ezeket az adatokat, kapjuk:
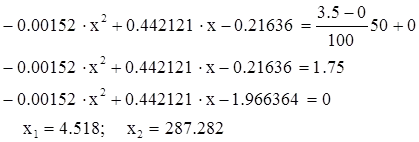
Válassza x1. azaz. a pillanatban, amikor belép a tartományban a kísérleti értékek. Behelyettesítve a értéke x1 (1.2), és megkapjuk az érték az erősítés 50% a névleges üzemmódban:
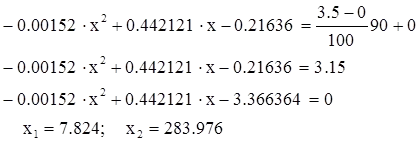
Mi az A értékét az átviteli együttható 90% az alábbi képlet szerint:
Válassza x1. azaz. a pillanatban, amikor belép a tartományban a kísérleti értékek. Helyettesítő x1 értéke (1,2), és így a értéke a nyereség 90% -a névleges mód:
A számítási eredmények a táblázatban.