Matekórán szög 10 vonalak között az űrben
A bezárt szög két egymást metsző egyenes vonalak mérjük a leírt módon síkrajzi (mert keresztül ezeket a sorokat lehet sík). Így a szög két egymást metsző vonal a térben a legkisebb a szögek által alkotott sugarai ezeket a sorokat a csúcspontot a metszéspontja.
A szög a két párhuzamos vonal úgy vesszük, hogy 0 vagy 180 °.
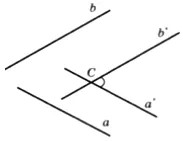
A szög két keresztező egyenes vonalak a és b jelentése a következő: bármilyen ponton C hajtjuk a'i gerendák b „úgy, hogy a || a „és b || b”. Ezután a szög között a „és b” vesszük egyenlő a szög ab. Más szóval, a vonalak a és b át egy új párhuzamos helyzetbe magukat átlépése előtt. Közelebbről, a C pont lehet venni az egyik vonal a és b, amely ebben az esetben rögzítve van.
Így a szög a sorok között az úgynevezett ferdeségi szög közötti metsző vonalak, illetve párhuzamos adat.
Merőleges egyenesek a térben
Két sor az úgynevezett merőleges az űrben, ha a köztük lévő szög a 0-90
Lemma: Ha az egyik a két vonal merőleges harmadik sorban, a másik vonal merőleges legyen erre sor.
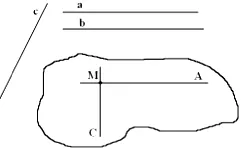
Miután t. M (M egy, M és M c) végezzen közvetlen MA és MB || a || c. Mivel a (a feltételezés), majd AMC = 90 ° -ra. A feltétel az a || b és MA || egy (az építési) azt jelenti, b || MA (a három párhuzamos vonalak tétel). Ezután a B és C vonalak párhuzamosak rendre MA és az MS közötti szög, amely 90 ° -ra b c, szükség szerint.
Ezt a vonalat nevezzük síkjára merőlegesen, ha merőleges bármely egyenes feküdt a gépen.
(Lehet rögzíteni: a α vagy α a).
Egy egyenes merőleges a sík metszi a sík.
és ai a b, a c, a d.
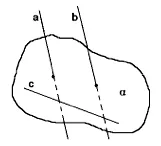
Ha a két párhuzamos vonal merőleges a síkra, a másik vonal is erre merőleges síkban.
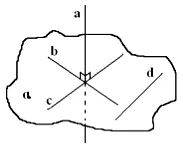
Döntetlen a síkban α egy tetszőleges sorban. Mivel egy α, majd (definíció szerint). Lemma, ha a merőleges c, és b, valamint párhuzamosan a merőleges. Mivel c - tetszőleges egyenes és merőleges a α (definíció szerint). QED.
Ha 2 vonalak síkjára merőlegesen, akkor párhuzamosak.
Ha egy sor nem hazudik merőleges síkban két egymást metsző vonal egy síkban van, akkor az egyenes és merőleges síkban.
m α, n α, m n = 0,1 m, 1 n
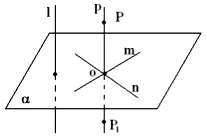
Rajzolj egy vonalat p úgy, hogy G p és p || 1. N 1 és p 1 || p n és p m. Legyen P és P1 - pontos vonal p oly módon, hogy az OP = OP1. Ezután, m és n - és így a szimmetriatengely, α - középső szimmetriasíkjához ezeket a pontokat, és így a p α. és p α p || január 1 α. QED.
A tulajdonságait merőleges vonalak és síkok:
- Keresztül bármely pontján tér sík merőleges az adott sort.
- Ha két A és B síkok merőlegesek a vonal egy, akkor azok párhuzamosak.
- Ha az egyik a két párhuzamos sík merőleges az egyenes vonal, és a másik sík merőleges erre a vonalra.
Tétel: Through bármely pontján tér nem tartozik a sík átmegy a merőleges erre a síkra, és csak egy.
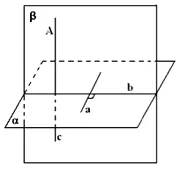
-
- Döntetlen a síkban α és az önkényes vonal konstrukció síkban β α, áthalad t β α = b β a sík a döntetlen egy vonalat |. c α (c β és szerkezet, például a β α). Tehát, hogy a kívánt vonalat.
- Lássuk be, hogy ez az egyetlen. Tegyük fel, hogy ez nem így van, és van egy közvetlen c1 alfa, majd a || c1. ez nem lehetséges, mert C1 = A. Így egy áthalad csak egy sor, hogy síkban α.
QED.