Mátrix algebra - ültették mátrix
Mátrix algebra - ültették mátrix

sorok rendre oszlopok ad az úgynevezett ültették mátrix dimenzió n × m:

Különösen, a strokitransponirovannoy vektor-mátrix, oszlopvektor
A fő tulajdonságai az átültetett mátrix:
1) kétszer ültették mátrixot egybeesik az eredeti:
2) az összege az átültetett mátrix mátrixok egyenlő az összege az átültetett mátrix kifejezések, azaz,
3) a transzponáltját mátrix termék mátrixok a termék az átültetett mátrix tényezők, hozott fordított sorrendben:
Egy négyzetes mátrix nyilvánvaló egyenlőség:
Ha a mátrix egybeesik annak transzponáltját
ez az úgynevezett szimmetrikus. Az utóbbi egyenletből következik, hogy a szimmetrikus mátrix tér és annak elemei is szimmetrikus a fő diagonális egyenlő:
Nyilvánvaló, hogy a termék egy szimmetrikus mátrix segítségével ingatlan 3, megkapjuk:
Példa Példa. Mivel az A mátrix és a transzponáltja a mátrix:
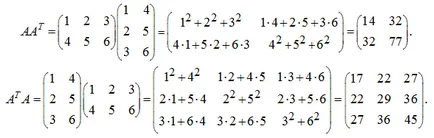
Ahogy az várható volt, kapott szimmetrikus mátrixok.