mátrix szorzás
Mátrixszorzással - az egyik leggyakoribb műveletek mátrixok. A mátrix, amelyet úgy kapunk, szorzás után az úgynevezett terméke mátrixok.
A terméket a mátrix Am × n mátrix, hogy Bn × k mátrix Cm × k olyan, hogy mátrix eleme C. található az i-edik sorban és j-edik oszlop, hogy az elem CIJ az összege a termékek elemek i -edik sorának A mátrix megfelelő elemek j-edik oszlopának mátrix B.
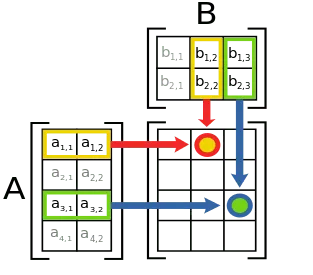
Process mátrixszorzással csak akkor lehetséges, ha az oszlopok száma az első mátrix a sorok számát a második mátrix.
például:
Lehetséges, hogy szaporodnak a mátrixban a mátrix?
m = n. Ez azt jelenti, megszorozva az adatok mátrix lehet.
Ha a mátrix felcseréljük, majd, az ilyen mátrixok, szorzás már nem lehetséges.
m ≠ n. így lehetetlen elvégezni a szorzást:
Elég gyakran megtalálható a munka egy trükk, ha a hallgató felkérik, hogy szaporodnak mátrixok. ami nyilvánvalóan nem lehet a szorzás.
Kérjük, vegye figyelembe, hogy néha lehet, hogy szaporodnak a matricát és így és így. Például, a mátrix, és esetleg szorzás MN. és szorzás NM.
Mátrixszorzással.
A művelet a mátrixszorzással - ez nem egy nagyon bonyolult művelet. Mátrix szorzást jobban megérthető konkrét példák, hiszen Csak meghatározása nagyon zavaró lehet.
Kezdjük egy nagyon egyszerű példa:
Meg kell szorozni. Először is, hogy a képlet ebben az esetben:
- van jó szabályszerűségét figyelhető meg.
Ezután egy bonyolultabb példa:
A képlet ebben az esetben :.
Mátrixszorzással eredmény:
Az eredmény egy úgynevezett nullmátrix.
Fontos megjegyezni, hogy nem működik itt „permutáció szabály helyezi a” szinte mindig MN ≠ NM. Ezért ami a műveletet a mátrix szorzás semmilyen esetben nem lehet felcserélni.
Most tekintsük példák mátrix szorzás a harmadik rend:
A képlet nagyon hasonlít az utolsó:
Szorzás egy mátrix egy szám.
Szorzás egy mátrix egy szám - ez ugyanaz a mátrix szorzás, kivéve, hogy ahelyett, hogy a második tömb vesszük elsődleges. Mint azt sejteni lehet, ez a szorzás sokkal könnyebb elvégezni.
Példa mátrix szorzás száma:
Itt minden világos -, hogy szaporodnak a mátrix egy szám. minden egyes eleme a mátrix kell egymás után szorozni egy meghatározott számot. Ebben az esetben - 3.
Egy másik hasznos példa:
- mátrix szorzás törtszám.
Az első lépés megmutatja, mit ne tegyünk:
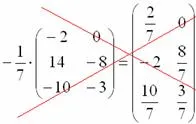
Ha egy mátrixot megszorozzuk egy törtszám nem kell semmilyen frakció a mátrixban, mivel ez elsősorban csak bonyolítja további intézkedéseket a mátrix, másrészt nehéz ellenőrizni a tanár megoldásokat.
És, sőt, nem szükséges, hogy elosztja az egyes eleme a mátrix -7:
.
Mit kellene tenni ebben az esetben - az, hogy kevesebb a mátrixban:
.
Ha lenne egy példát, amikor az összes elemet a mátrix lenne osztva 7 maradék nélkül, akkor lehet (és kell!) Kell osztani.
Ebben a példában, ez lehetséges és szükséges, hogy megszorozzuk az összes mátrix elemeinek a ½, hiszen minden egyes eleme a mátrix osztható 2 maradék nélkül.
Megjegyzés: a magasabb matematika iskola koncepciója „osztály” nem elmélet. Ehelyett az „ez van osztva” akkor mindig azt mondják, „ez kell szorozni egy töredéke.” Azaz, a szétválás - ez egy speciális esete a szorzás.