Megoldása rendszerek lineáris egyenletek hozzáadásával
Megoldani egy lineáris egyenletek két változó hozzáadásával, szükség van:
1) szorozzuk mindkét oldalán az egyik vagy mindkét a egyenletek egy számot, hogy az együtthatók az egyik változót az egyenlet ellentétes lesz szám;
2) slozhitpochlennopoluchennye egyenletek és megtalálják az értéke az egyik változó;
3) Behelyettesítve az értéke egy változó az egyik ilyen egyenletek és megtalálni az érték a második változó.
Ha ez a rendszer együtthatók egy változó ellentétes számok, a rendszer azonnal megkezdődik, amint az oldatot a 2. lépésben).
Példák. Oldja meg a rendszer lineáris egyenletek két változó hozzáadásával.
Mivel az együtthatók az Y ellentett (-1, 1) a kiindulási oldatot a 2. lépéstől). Mi összeadjuk Terminusonként az egyenlet, és megszerezni a következő egyenlettel 8x = 24. A második rendszer egyenletek írhatók bármely egyenlet az eredeti rendszer.
Találunk x és helyettesíti az értéket a második egyenletben.
Megoldása a második egyenletet használva: y 9 = 14, ezért y = -5.
Mi egy átvilágítás. Behelyettesítve x értékei = 3 és y = -5 az eredeti egyenletrendszer.
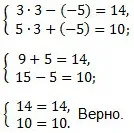
Ha megszorozzuk az első egyenletet (-2), az együtthatók az x változó lesz ellenkező számok:
Ha ezeket az egyenleteket Terminusonként.
Majd kap az egyenértékű egyenletrendszert, amelyben az első egyenlet összege az előző két egyenletrendszert, és a 2. egyenletrendszert írunk az első egyenletben az eredeti rendszer (az egyenlet általában írva egy kisebb együtthatót):
Találunk érkező 1. egyenlet, és a kapott értéket behelyettesítjük a második.
Megoldása az utolsó egyenlet és szerezzen X = -2.
Azt, hogy a változó együtthatója y ellentétes számokat. Ebből a célból minden tagja az 1. egyenlet megszorozzuk 5, és minden tagja a 2. egyenlet 2.
Behelyettesítve x érték = 4 a második egyenletben.
3 × 4 - 5Y egyszerűsítik = 27. 12 - 5Y = 27, így -5u = 15 és y = -3.