Mi az átlós kocka, és hogy hogyan lehet megtalálni

Mi az a kocka, és amit ő átlós

Cube (szabályos poliéder vagy kocka) egy háromdimenziós ábrát, minden arc - ez egy négyzet alakú, amely, mint tudjuk, minden oldalról egyenlő. kocka átlója egy szegmens, amely áthalad a központ a szám, és csatlakoztassa szimmetrikus csúcs. A jobb oldali kocka átlója 4 és ezek mind egyformák. Fontos, hogy ne keverjük össze az átlós a figura magát a diagonális arc vagy négyzet, ami fekszik tövében. A kocka átlóját középpontján átmegy az arc és összeköti a szemközti csúcsa a tér.

Formula, hogy megtalálja az átlós kocka

Átlós rendszeres poliéder megtalálható egy nagyon egyszerű képlet, hogy azt szeretnénk, hogy emlékezzen. D = a√3, ahol D jelentése az átlós a kocka, és - ezt a peremet. Itt egy példa a probléma, ahol meg kell találni a diagonális, ha tudja, hogy ez egyenlő a szélén 2 cm hosszban. Ez egyszerű D = 2√3, nem is kell vizsgálni semmit. Egy második példa, hagyja, hogy a szélén a kocka egyenlő √3 cm, akkor azt kapjuk, D = √3√3 = √9 = 3. Válasz: D = 3 cm.

Formula, hogy megtalálja az átlós kocka

Diago

Nahl metszettel is megtalálhatók a következő képlettel. Diagonals, amelyek ellen az arcán mindössze 12 darab, és ezek mind egyformák. Most emlékszem d = a√2, ahol d - az a négyzet átlója, és - ez is egy kocka éle vagy a tér két szélén. Ahhoz, hogy megértsük, ahol ez a képlet nagyon egyszerű. Miután az összes, a két oldalán a tér és a diagonális formája egy derékszögű háromszög. Ez a trió szerepét játssza egy átlós átfogója és az oldalán a tér - ez a lábait, hogy az azonos hosszúságú. Emlékezzünk a Pitagorasz-tétel, és egyszerre a helyére kerül. Most a probléma: kocka éle egyenlő √8 látni, meg kell találni a diagonális annak arcok. Helyezünk a képlet, és azt kapjuk d = √8 √2 = √16 = 4. Válasz: Az átlós kocka 4 cm.

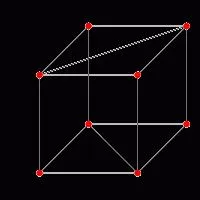
Ha tudjuk, hogy az arcok a kocka átlós

Nyilatkozata szerint a probléma, mi kapnak csak az átlós arca szabályos poliéder, amely egyenlő, mondjuk, √2 cm, és meg kell találnunk egy átlós kocka. A képlet, hogy megoldja ezt a problémát egy kicsit bonyolultabb az előző. Ha tudjuk, hogy d, akkor meg tudjuk találni a szélén a kocka, alapján a második képlet d = a√2. Kapunk egy = d / √2 = √2 / √2 = 1cm (ez a mi él). És ha tudjuk, ezt az értéket, akkor megtalálja a kocka átlós nem nehéz: D = 1√3 = √3. Így megoldottuk a feladatot.

Ha egy ismert felületű

Az alábbi algoritmus megoldást találni átlósan a felületre a kocka. Tegyük fel, hogy ez a 72 cm 2. Ahhoz, hogy megtalálja az elején a terület egyik oldalán, és összesen 6 Ezután 72 kell osztani 6, megkapjuk 12 cm 2. Ez a terület az egyik oldalán. Ahhoz, hogy megtalálja a szélén egy szabályos poliéder, szükséges felidézni a képlet S = a 2. olyan = √S. Helyettesítő és kapjunk = √12 (kocka él). És ha tudjuk, ez az érték, és nem nehéz megtalálni egy átlós D = a√3 = √12 √3 = √36 = 6 Válasz: Az átlós kocka egyenlő 6 cm 2.

Ha ismert hosszúságú kocka élei

Vannak esetek, amikor a probléma adják csak a hossza az összes szélei a kocka. Ezután meg kell osztani 12. Ez a szám a felek rendszeres poliéder. Például, ha az összeg az összes élek megegyezik a 40, egyik oldalán lesz egyenlő 40/12 = 3.333. Azt hogy az első formula és kap a választ!