Modellezése véletlen vektorok - studopediya
Véletlen vektor (valószínűségi változók rendszer) halmaza véletlen változók, amelyek együttesen jellemzik a véletlen jelenség
ahol Xi - CB bizonyos jogszabályok forgalmazás.
Ez a tétel tartalmaz egy anyagot, módszerek szerint modellezésének folyamatos véletlen vektorok (mindazon elemek, amelyek folytonos NE).
Kimerítő jellemző véletlen vektor többdimenziós együttes eloszlásfüggvénye összetevői F (x1, x2,. Xn) vagy a megfelelő együttes sűrűségfüggvény többdimenziós
A legegyszerűbb módja annak, hogy szimulálja a véletlen vektor független komponensek, amely kielégíti
azaz Mindegyik véletlenszerű komponens vektor lehet szimulálni a másiktól függetlenül szerint a „saját” valószínűség-sűrűség fi (xi).
Abban az esetben, ha a véletlen vektor komponenseinek statisztikailag független, akkor szükséges speciális módszerek: feltételes eloszlás, kivételek (Neumann), lineáris transzformációk.
hagyományos terjesztési módszerek. A módszer azon alapul, rekurzív számítása a feltételes valószínűség sűrűség minden egyes eleme a véletlen vektor X együtt egy többdimenziós sűrűségfüggvénye f (x1. X2, ..., xn).
A sűrűség eloszlását véletlen vektor x felírható:
Ezekre integrációs sűrűség szükséges közös véletlen vektor sűrűség eloszlása az egyes tartományok:
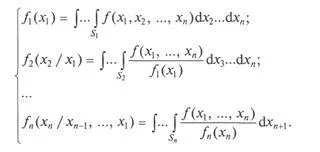
Módszer feltételes eloszlások (inverz függvény módszer skalár CB) lehetővé teszi, hogy figyelembe veszi az összes statisztikai tulajdonságait a véletlen vektor. Ezért csak egy következtetés: ha ez lehetséges a feltételes eloszlás sűrűség fn (. Xn / xn-1, xn-2. X1), akkor használja ezt a módszert.
eliminációs módszer (Neumann). A módszer egy általánosítása módszer figyelembe CB Neumann esetében n változók. Feltételezzük, hogy az összes komponens egy véletlen vektor elosztva véges intervallumban xi [ai. bi], ahol i = 1, 2 n. Ha nem, akkor kell, hogy vágni a eloszlási sűrűsége a jelen körülmények között.
Az algoritmus a következő módszerrel.
1 generáltunk (n + 1) PRNG
illetve elosztott időközönként
2. Ha a feltétel
Ez a szükséges megvalósítása véletlen vektort.
3. Ha ez a feltétel nem teljesül, menj az első tétel, stb
Ábra. 10.14 tartalmaz egy illusztráció az algoritmus a kétdimenziós esetben Rf £ F (R1, R2).
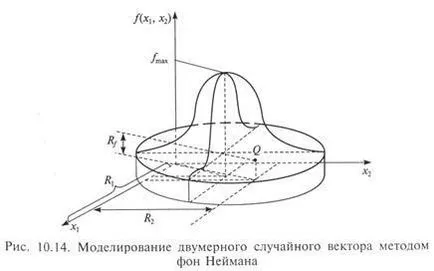
Vissza a n. 1. után a „sikertelen” n PSCH szimuláció úgy történik, amikor a Q pont lesz nagyobb felületi képviselő kétdimenziós valószínűségi sűrűségű f (x1. X2). Abban az esetben, az ábrán látható, a (rendes) kétdimenziós megvalósítása a véletlen vektor kell venni PSCH pár (R1, R2).
Átlagos relatív gyakorisága a „hiba” lehet kiszámítani geometriailag azáltal, hogy a térfogati aránya a megfelelő számok.
Mint már említettük egydimenziós esetben a fő előnye az eljárás von Neumann sokoldalúságát. Azonban a valószínűsége sűrűsége, amelynek a felületén éles csúcsokat fog bekövetkezni elég gyakran az „üres” működik, ha a következő PN n elutasítják. Ez a hátrány a jelentősebb, a legnagyobb mérete a szimulált vektor (n) és hosszabb, mint a szükséges mintát megvalósításai a véletlen vektor. A gyakorlatban az ilyen helyzetek nem túl gyakran fordul elő, így a folyamat megszüntetése, és olyan széles körben elterjedt.
A módszer a lineáris transzformációk. A módszer a lineáris transzformációk egyike a leggyakoribb úgynevezett korrelációs eljárások alkalmazni abban az esetben, amikor a szimuláció folyamatos n-dimenziós véletlen vektor elég, hogy csak a szükséges értékeit az elemek a korrelációs mátrix a vektor (ez különösen fontos abban az esetben, a normális eloszlás, amelyre a végrehajtási követelményeket a cím ez azt jelenti, nyilvánított elégséges feltétele a teljes véletlen egybeesése elméleti és szimulált disztribúciók). Az az elképzelés, a módszer a lineáris transzformációja n-dimenziós véletlen vektor Y cnezavisimymi (gyakran normális eloszlású) komponenseket a véletlen vektor X a kívánt korrelációs mátrix és egy vektor összetevője matematikai elvárásoknak.
A matematikai megfogalmazása a probléma a következő. Tekintettel a korrelációs mátrix, és a várakozás vektor X
Azt akartuk, hogy megtalálják a B mátrix, amely lehetővé tenné az átalakulás
ahol Y - n dimenziós vektort független komponensek normális eloszlású standard paraméterek, vételi vektor X strebuemymi jellemzőit.
Arra törekszünk, a mátrix B, mint egy alsó háromszög mátrix, mind az elemeket, amelyek, fölött elrendezett a fő diagonális vannak 0. folytassa mátrix formában a rendszer algebrai egyenletek:
Mivel a komponensek a vektor Y függetlenek és standard paraméterek, a következő kifejezést tartja
Beszorozva Terminusonként maguknak és egymásnak, illetve a bal és jobb oldalán az egyenleteket (3.2) és megszorozzuk az eredményt figyelembe az elvárás, megkapjuk az egyenletrendszert
Amint az könnyen látható, a bal oldalán a egyenletek kapott - elemek adott korrelációs mátrix Q, aB jobbra - az előírt mátrix elemeinek B. Ezt követően megoldása ezt a rendszert, megkapjuk a képlet számítási elemek bij:
A képlet kiszámításához minden egyes eleme a transzformációs mátrix B formájú
Így az algoritmus a lineáris transzformációk igen egyszerű:
· Egy előre meghatározott értéke a korrelációs mátrix számított konverzió együttható V mátrix;
· Létrehoz egy végrehajtása az y vektor, melynek összetevői függetlenek és normális eloszlású standard paraméterek;
· A kapott vektor helyettesítik be az expressziós (3.1), és meghatározzák a következő végrehajtása az X vektort, amelynek egy előre meghatározott korrelációs mátrix és egy vektor matematikai elvárások komponenseket;
· Ha szükséges, az előző két lépést az algoritmus ismétlődnek szükséges számú alkalommal (és így a kívánt mennyiségű vektor X implementációk).
Ebben a fejezetben, az alapvető módszer a álvéletlen egyenletesen elosztott [0; 1], és szimulációja véletlenszerű események, változók és vektorok, általánosan használt, a gyakorlatban a szimulációs vizsgálatok EIS. Általános szabály, hogy minden modern szoftver eszközök végrehajtásához használt ilyen szimulációs modellek beépített generátor egyenletesen elosztva Pszeudovéletlen, amely lehetővé teszi, hogy a kutató könnyen szimulálni bármilyen véletlenszerű tényezők.