Módszer egyszerű iteráció
A módszer egyszerű iteráció a számítás az új pont x a régi pont.
Az iteráció addig folytatódik, amíg a kívánt megoldás pontossága ε.
[Edit] döntési algoritmus
Input: A, B, ε.
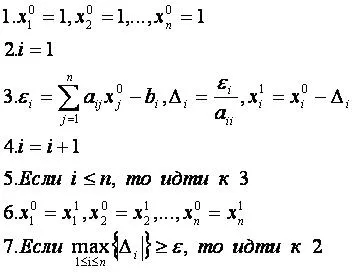
Output: x.
A megoldások egyszerű iterációk lineáris egyenletek Ax = b rendszer (ahol A - NxN négyzetes mátrix együtthatók, és b - vektor ingyenes tagok a rendszer), először megtalálni a fő meghatározó Δ rendszer.
Módszer egyszerű iterációk alkalmazható (azaz konvergens módszer), ha a fő meghatározója a rendszer Δ ≠ 0 és feltételei a két esetben:
1), amikor legalább az egyik a normák a mátrix B = E-A jelentése kevesebb, mint 1:
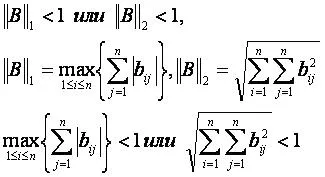
2) amikor az összes sajátértékei a mátrix B = E-modulusa kisebb, mint 1.
Hogy ellenőrizze a feltételeket, a 2. esetben van szükség, hogy meghatározzuk az értéke λ = Max1 |, | λ2 |, ..., | λn |>. ahol λ1, λ2, ..., λn - sajátértékei B. és ellenőrizze a λ<1 .
Tipikusan a mátrix B = E-A kielégíti a fenti feltételeket, amikor a fő diagonális A mátrix a domináns elemek AII;
Ali domináns elem az elem kielégíti a egyenlőtlenséget: