Nem tradicionális szorzata több számjegyű számokkal

Kutatás matematika az általános iskolában

„A téma a matematika olyan súlyos, hogy érdemes, hogy ne veszítse néhány esetben teszi szórakoztató.”
B. Pascal
bevezetés
Egy ember a mindennapi életben nem nélkülözheti a számítástechnika. Ezért matekórán vagyunk, elsősorban tanítják, hogy végre műveleteket szám, ez tekinthető. Mi szorzás, osztás, összeadni és kivonni, mi ismerős minden módon, hogy tanítják az iskolában. Felmerült a kérdés: van-e még olyan alternatív számítási módszerek? Azt akartam, hogy tanulmányozza azokat részletesebben. A keresés a választ a kérdésekre, ezt a vizsgálatot.
Célkitűzés: azonosítani innovatív módon szaporodni, hogy tanulmányozza a kérelmet.
Összhangban azzal a céllal, fogalmaztuk a következő feladatokat látja el:
- Keresse meg annyi szokatlan módon szorzás.
- Megtanulják, hogyan kell alkalmazni őket.
- Maguk választhassák ki a legérdekesebb vagy világosabb, mint a kínált az iskolában, és használja őket, hogy figyelembe.
- Ellenőrizze a gyakorlatban megszorozzuk több számjegyű számokkal.
- Végezzen felmérést a hallgatók évfolyamon 4
A vizsgálat tárgya: különféle nem szabványos algoritmusok megszorozzuk több számjegyű számokkal
Kutatási téma: matematikai művelet „szorzás”
Hipotézis: ha van szabvány módon szaporodnak több számjegyű számokkal, talán vannak más lehetőségek is.
Relevanciáját. tudás terjesztésének alternatív módjait szorzás.
A gyakorlati jelentősége. A munka során úgy döntöttek, sok példa, és az album jön létre, amely magában foglalja a példákat a különböző algoritmusok szorzatából multidigit számok több alternatív módszer. Ez érdekes lehet bővíteni osztálytársai matematikai kilátások és lesz a kezdete az új kísérletek.

1. fejezet Alternatív módszerek szorzás

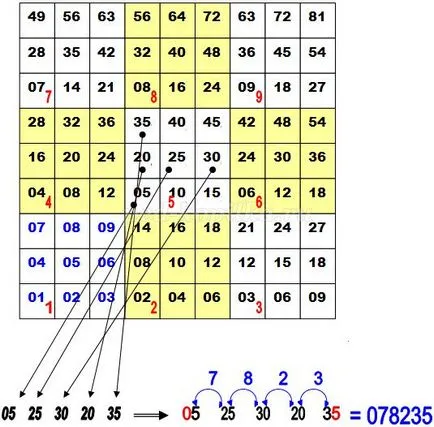
1. függelék A módszer Paraszt

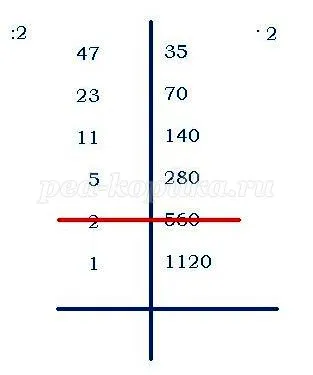
2. függelék Little Castle

Melléklet 3. Rács

4. Kínai alkalmazási módszerrel (grafikus)

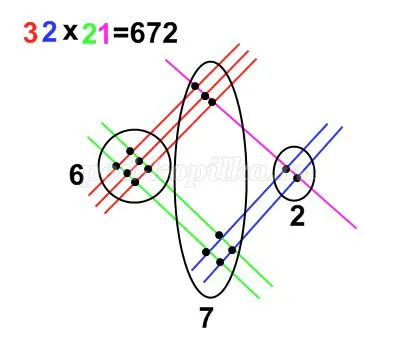
Függelék 5.Yaponsky módszer (körök)

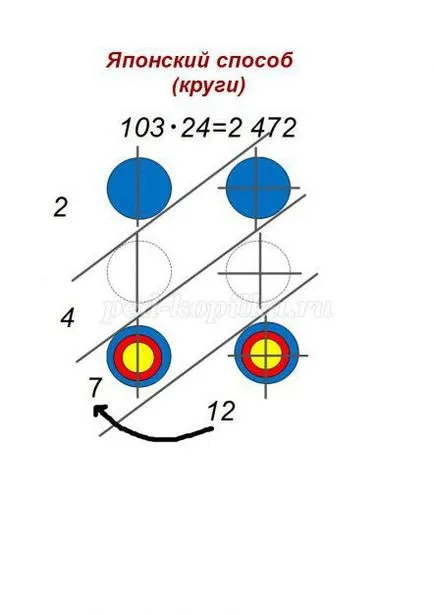
6. függelék táblázat Basil Okoneshnikova