Oktatási alkalmazása numerikus módszerek közelítése függvényében

köbös spline módszerrel

A kifejezés eredete „spline” van csatlakoztatva egy rugalmas vonalas rajz, amelyet használt rajz sima íveket átmenő adott pontot.

Spline interpoláció - egy gyors, hatékony és fenntartható módon interpolációs funkciókat. Együtt racionális interpoláció spline polinom interpoláció alternatívák [28].

Az alap spline interpoláció alapján a következő elvet. interpoláció intervallum osztva kis szegmensek, amelyek mindegyike meghatározott polinom függvény a harmadik foka. A polinom együtthatóit úgy választjuk meg, hogy kielégítenek bizonyos feltételeket (amely függ az interpolációs módszer). Közös minden típusú harmadrendű spline követelmények - folytonos függvények, és természetesen, a folyosón keresztül a pontokat hozzárendelve. További követelmények lehet egy lineáris függvény csomópontok közötti, a folytonosság a magasabb származékok, stb

A fő előnye a spline interpoláció a stabilitás és az alacsony komplexitás. Lineáris egyenletrendszer, amelyet meg kell oldani ahhoz, hogy építeni görbék, nagyon jól kondicionált, amely lehetővé teszi, így az együtthatók polinomok nagy pontossággal. Ennek eredményeként, még a nagyon nagy N számítási rendszer nem veszít a stabilitást. Építőipari együttható táblázat spline O (N) műveletek, és értékének kiszámításánál a spline egy adott pontban - csak

Általában köbös polinom spline kiválasztott

meghatározott tartományban.

Az egész görbe egy sor köbös polinomok (1.4 ábra) a megfelelően kiválasztott együtthatók - spline paraméter [20, 38].

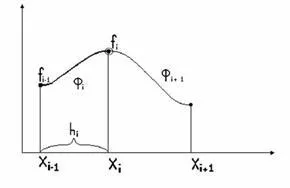
1.4 ábra: rendszere spline módszerek

Az együtthatókat az egyes intervallumok meghatározzuk az átviteli feltételek a csomópontok:

Ezen túlmenően, a határon, ha a feltételek beállítása és

Arra törekszünk, egy harmadfokú polinom formájában

A feltétel van

és megkövetelik a folytonosság.

A teljes száma ismeretlen együtthatók nyilvánvalóan egyenlő. száma egyenletek (1,13) és a (1.14) egyenlő. Hiányzik két egyenlet jutunk el (1,12) u.

Expression (1.14). Behelyettesítve ezt a kifejezést az (1.13) és kizárva. kapjuk:

Most helyettesítve kifejezéseket az első + általános képletben (1,14), miután az egyszerű transzformációk meghatározására másodrendű egyenlet:

A peremfeltételek:

És a feltétel egyenértékű az egyenlet. A különbség-egyenlet (1.15) feltételek (1,16) is megoldható a sweep módszerrel, képviseli, mint a rendszer lineáris algebrai egyenletek formájában. ahol a vektor megegyezik a vektor. vektor F elemenkénti jobb oldalán egyenlet (1,15), és a mátrix a következő formában:

söpörni módszer azon a feltételezésen alapul, hogy az ismeretlen ismeretlenek kapcsolódik a rekurzív sorozat:

Ezzel kapcsolatban, ki tudjuk fejezni, és keresztül-helyettesíti i-e egyenlet:

ahol - a jobb oldalon az i-edik egyenlet. Ez a kapcsolat lehet elvégezni, függetlenül a döntés, ha szükség van rá:

Az első egyenletet kapjuk:

Miután megtalálta és progonochnyh együtthatók. egyenlet alkalmazásával (1), így a megoldás a rendszer. Ugyanakkor,

Spline interpoláció jó, mert ismereteket igényel csak a csomópontok a funkció, de nem annak származékai [34, 36, 43].