oldatot származékok
Ahhoz, hogy megértsük a származékos ügylet definíciójának, úgy az alábbi grafikon a funkciót.

1. ábra. Egy példa a funkció és annak származéka.
Nézzük a képen látható helyeken, ahol a funkció gyorsan növekszik, és hol csökken. Például, a b pont az a pont egy grafikon emelkedik gyorsabban, mint a b pont, hogy a C pont.
Ha mozog a lényeg, hogy a függvény grafikonját az új koordináta-rendszert oly módon, hogy növelje a pont fölött helyezkedik el a tengely és az X pont alá süllyed az x tengely (következő skála), és csatlakoztassa a pontok, akkor kap egy új menetrendet az új funkciók (alsó ábra szerinti. 1 ). Ez a funkció a származék elsődleges funkciója. Ez a grafikon semmit, indikátora a változás mértéke funkciókat. Más szóval, a származtatott - sebességváltozás funkciót. A gyakorlatban a származékok meghatározására használt változási sebessége egyes folyamatok: a fizikai, kémiai, gazdasági, stb
A bonyolultabb nyelvet, a származék - a határ, amely felé az arány a növekmény a növekmény x y. Általában, differenciálhányados néz ki, és meghatározása a következő:
A folyamat a számítástechnikai differenciálhányados nevezzük differenciálásával.
Funkciók talált a gyakorlatban nagyon sok, de van egy egyszerű függvény (alap), mint például, az F (x) = sinx, F (x) = C (ahol C egy állandó), F (x) = LNX stb Ezekre elemi függvények már definiált származékai és elég nekik, hogy megtanulják a szíve. Egyszerű származékok (alap) funkciók vannak megadva az alábbi táblázatban.
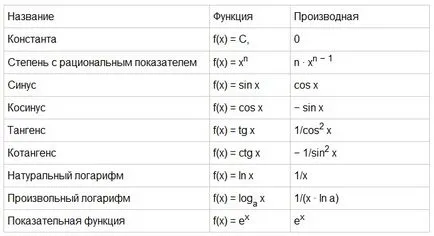
2. ábra. Táblázat egyszerű származékai (alap) funkciók.
Megoldás-származékok. egyszerű szavakkal, ez az, hogy kapcsolja egy funkció, hogy egy másik, következő bizonyos szabályok (a kivétel az exponenciális függvény F (x) = e ^ x, amely nem változik).
Vegyünk egy példát. Meg kell találni a függvény deriváltját F (x) = x ^ 3 + 3x ^ 2 - 72x + 90
Ahhoz, hogy megoldja a származék elegendő, hogy az asztal származékok egyszerű (elemi) funkciókat. Összhangban a táblázat adatai, így a származék:
F '(x) = (x ^ 3 + 3x ^ 2 - 72x + 90)' = 3x ^ 2 + 6x-72
A megoldás komplex-származék
A gyakorlatban a döntést a származékok összetett funkciók szembe kell néznie gyakrabban, mint egyszerű.
A szabály meghatározására származékot egy összetett függvény a következő:
(A (b)) '= a' (b) * b”, ahol egy külső-funkciót, b-belső funkciója.
Meg kell találni a függvény deriváltját F (x) = sin (3x-5)
Keresse meg a származékot ezt a funkciót használja az asztal az egyszerű (elemi) funkció nem működik, mint egy bűn van egy egész kifejezés, azaz funkció két funkció a = sin (x) (külső függvény) és b = 3x-5 (belső funkció).
Mi a szabályt meghatározása származékot egy összetett függvény és szerezzen:
F '(x) = (sin (3x-5))' = cos (3x-5) * (3x-5) „= 3cos (3x-5).
Ha az anyag hasznos volt otblagorit honlapunkon tudsz, azáltal, hogy egy adomány.
Bármilyen mennyiségű fejlesztési projekt, akkor adományoz ezen az oldalon.