ortogonalizációs módszer
Gram-Schmidt ortogonalizáció - az egyik módszer, amelyben alapuló több lineárisan független vektorokat ortogonális vektorok vagy ortonormált vektorok, és úgy, hogy minden vektor vagy fejezhető ki lineáris kombinációjával vektorok. Ez a folyamat lehet használni ahhoz, hogy a QR-bomlás. amely rendszerben az eredeti vektor képezi az oszlopok az eredeti mátrix és a mátrix oszlopait Q nyert egy sor a ortogonalizáló vektorok. Így, ellentétben Givens módszerek (forgatások) és Householder (reflexiók) alapján a csökkentésére a mátrix bal egységes / ortogonális transzformációk háromszög alakú, ortogonaiizáió alapuló technika csökkentésére a mátrix jobb nonorthogonal (azt mondhatjuk, háromszög) átalakítja az egységes / ortogonális átlagos .
A matematikai módszer alapján
Classic ortogonalizációs módszer meglehetősen egyszerű, azonban, mivel a bizonytalanság nyilvánul meg a nem-ortogonalitásának kapott csak nagyon ritkán használják a gyakorlatban.
Tegyük fel, hogy lineárisan független vektorok. Tegyük fel, hogy a nyúlvány egy vektor meghatározása a következő:
ahol - a skaláris szorzata vektorok.
A skaláris szorzata két vektor a k-dimenziós valós térben definíciója:
.
Ez az operátor vetíti vektor kollineáris vektor.
A ortogonalitását vektorok érjük lépésben (2).
Gram klasszikus eljárás - Schmidt a következő:
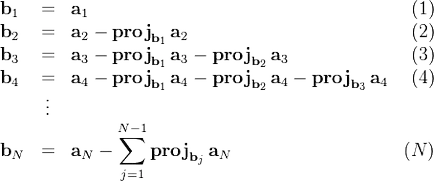
Alapján minden egyes vektor állítható elő egy normált vektor (Y normált vektor iránya ugyanaz, mint az eredeti, és a norma - egység). A norma a képlet - megállapodott a skalár szorzat:
Az eredményeket a folyamat Gram - Schmidt:
- egy olyan rendszer ortogonális vektorok vagy
- egy olyan rendszer ortonormált vektorok.