Ősi módszerek szorzás
„Számla és számítás - az alapja a rend a fejében.”
Pestalozzi
- Megismerkedhetnek a régi módszerek szorzás.
- Ismeretek bővítése különböző módszerek szorzás.
- Tanulás, hogyan kell műveleteket végeznek a természetes számok, az ősi módszerek szorzás.
A sürgősségi használatának gyors számolás technikákat.
A modern élet, minden ember gyakran el kell végeznie egy nagy szám a számítások és a számítások. Ezért a Munkám célja - megmutatni könnyű, gyors és pontos számolási módszer, hogy nem csak segít a számításokat, de okoz jelentős meglepetés barátai és kollégái, mivel a szabad végrehajtása megszámlálható műveletek nagymértékben utalhatnak, az eredetiség, az intelligencia. Alapvető eleme a számítógépes kultúra tudatos és erős számítógépes ismeretek. A probléma kialakulásának számítógépes kultúra szempontjából lényeges az egész iskola matematika, kezdve az általános iskolai, és többre van szükség mastering számítási készségek, és használja őket a különböző helyzetekben. Birtoklása számítási képességek és készségek nagy jelentősége van az asszimiláció az anyag vizsgált, lehetővé teszi, hogy értékes munkaerő minősége: a felelősségteljes magatartás a munkájukat, az képes felismerni és kijavítani a hibákat tett a munkát, pontos feladat végrehajtását, kreatív hozzáállás munkaerő. Ugyanakkor az elmúlt években a szintű számítógépes ismeretek, kifejezések átalakulás kifejezett csökkenő tendenciát mutat, a hallgatók számára megengedett egy csomó hibát kiszámításakor, minden egy számológép gyakran nem racionális gondolkodási, ami negatívan befolyásolja a képzés minőségét és szintjét a matematikai tudás hallgatók egészét. Ennek egyik eleme a számítógépes kultúra orális fiókot. ami nagyon fontos. Az a képesség, hogy gyorsan és helyesen elvégezni egyszerű számításokat „az elme” van szükség minden egyes személy.
Ősi módszer a szorzás a számok.
1. A régi módon meg kell szorozni 9 ujjaival
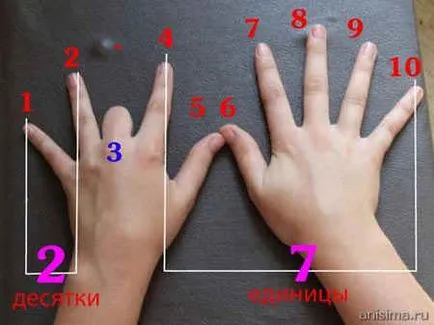
Ez egyszerű. Szorzáshoz bármennyi 1-9 9-én, nézd meg a kezét. Fold az ujj, amely megfelel szaporodnak (például 9 x 3 - szor a harmadik ujját), számítanak ujjaival a hajtogatott ujját (abban az esetben, 9 x 3 - a 2), majd kiszámítja a hajtogatott, miután az ujj (a mi esetünkben - 7). Válasz - 27.
Mert szorzó egységek szaporodnak egység működik pereumnozheniya szorzók, hogy készítsen több egy tucat szorozni az egységnyi más és fordítva, és az eredményeket a redőzött száz szorozva tíz. Módszer Ferrolban könnyen szaporodnak orálisan kétjegyű szám 10-20.
b) 1x4 + 2x1 = 6, levelet 6
Ez a technika hasonlít szorzás egy oszlop, de elég hosszú.
Fogadási. Mondjuk kell szorozni 13 24. Rajzolj egy alábbi ábra:
Ez a rajz áll 10 sor (a szám lehet használni)- Ezek a vonalak jelzik a száma 24 (2. sor, francia, 4. sor)
- Számos ilyen vonalak képviselik a 13 (1 vonal, francia, 3. sor)
Most ki kell számolnunk a kereszteződésekben a vonalak mind a négy sarkában az alábbiak szerint:
(Metszéspontja az ábra által jelzett pontok)

- A felső bal szélén: 2
- Engedje le a bal szélén: 6
- Jobb felső: 4
- Jobb alsó: 12
1) A csomópontok a felső bal széle (2) - egy első számú válasz
2) Az összeg a keresztezések a bal alsó és a jobb felső élei (6 + 4), - egy második számú válaszüzenetet
3) A kereszteződéseket a jobb alsó szélén (12) - a harmadik szám a válasz.
Úgy kapjuk: 2; 10; 12.
mert utolsó két szám - két számjegyű, és nem tudjuk írni őket, akkor írj csak néhány, és hozzáadjuk az előző tíz.
4. Az olasz módszer szorzás ( „Grid”)
Olaszországban, valamint számos országban a keleti, ez a módszer tett szert nagy hírnévre.
Például szorozzuk 6827 345.
1. Felhívjuk négyzetháló és írjon egy számot az oszlopok felett, és a második legmagasabb.
2. Szorozzuk száma minden sorban egymás után a számok az egyes oszlop.
azaz- 6 * 3 = 18. Write 1 és 8
- 8 * 3 = 24. Write a 2 és 4
Ha a szorzás a egyjegyű számot kapunk, írunk tetején 0, alatt és ezt a számot.
(Mivel a példánkban, ha szorozva 2-3 fordult 6. A tetején a felvett 0, és kisebb, mint 6)
3. Töltsük ki a teljes hálózatra, és add fel a számokat, miután az átlós csíkokkal. Elkezdjük rendbe. Ha az összeg egy átlós tartalmaz több tucat, akkor add hozzá a következő egységeket átlós.
Ez a módszer a szorzás által használt magyar gazdák körülbelül 2-4 évszázaddal ezelőtt, és fejlesztették az ókorban. A lényege ennek a módszernek a: „Amennyire tudjuk osztani az első tényező, hogy szaporodnak, mint a második” .Vot például: Meg kell szorozni 32 13. Itt van, hogyan kell kiválasztani a példáját 3-4 évszázaddal ezelőtt őseink:- 32 * 13 (32 osztva 2, és a 13 többszörösen 2)
- 16 * 26 (16 osztva 2, és a 26 többszörösen 2)
- 8 * 52 (stb)
- 4 * 104
- 2 * 208
- 1 * 416 = 416
Bisection folytatni, amíg a saját nem kapcsol 1, párhuzamosan a duplájára száma egyaránt. Nemrég megduplázódott a számot, és adja meg a kívánt eredményt. Nem nehéz megérteni, hogy mi az eljárás alapul: a termék nem változik, ha az egyik tényező az, hogy csökkentse a felére, a másik fele a növekedés. Egyértelmű tehát, hogy ennek eredményeként a gyakori ismétlés E művelet, a kívánt terméket
De mi a teendő, ha ez szükséges, hogy felére csökkentik a száma páratlan? Népi módon könnyen jön ki ez a probléma. Szükséges, - így szól a szabály - abban az esetben, páratlan szám és az eldobott egység osztja ketté a maradékot; de az utolsó napon a jobb oldali oszlopban kell hozzá a számokat ebben az oszlopban, amely úgy áll szemben a páratlan számok a bal oldali oszlop: Az összeg a szükséges munkát. A gyakorlatban ez teszi, hogy az összes vonalak páros számok a bal kihúz; csak azok, amelyek páratlan számú balra. Itt egy példa (a csillaggal jelölt ezen a vonalon kell húzni):- 19 * 17
- 9 * 34
- 4 * 68 *
- 2 * 136 *
- 1 * 272
- 17 + 34 + 272 = 323.
Egy ilyen eljárás a szaporodás ókori Indiában.
Szorzáskor például 793-92 írjon egy számot a szorzó és alatta a másik pedig egy tényező. Hogy könnyebb navigálni, akkor egy háló (A) példaként.
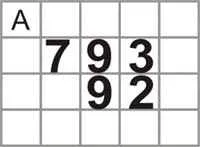
- 1. szabály Az egység az első működik írandó ugyanabban az oszlopban a szorzó, azaz ebben az esetben a 9.
- 2. szabály az alábbi munkálatok kell írni oly módon, hogy az egységek vannak elhelyezve az oszlop közvetlenül jobbra a korábbi munkát.
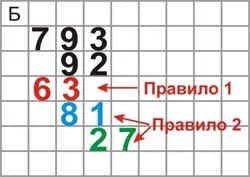
Ismételjük meg az eljárást a többi szorzó számok, ugyanazokat a szabályokat követi (C).
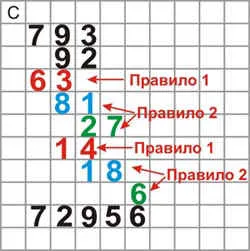
Majd összeadjuk a számokat az oszlopok és megkapja a választ: 72956.
Mint látható, kapunk egy nagy a termékek listáját. Az indiánok, akik a sok gyakorlás, írta minden számjegy nem a megfelelő oszlopba, és a tetején, amennyire csak lehetséges. Ezeket azután egymásra oszlopok és a számok kapott eredmény.
Léptünk az új évezredben! Grand felfedezések és eredmények az emberiség. Tudjuk, hogy sok, sok lehet. Úgy tűnik, hogy valami természetfeletti, hogy segítségével a számok és képletek, ki tudjuk számítani a repülés az űrhajó, a „gazdasági - helyzet” az országban, az időjárás „holnap”, hogy leírja a jegyzeteket dallamot. Tisztában vagyunk azzal, a nyilatkozatot a görög matematikus és filozófus, aki élt a 4. században d n.e.- Püthagorasz -. „Minden szám”.
Szerint a filozófiai nézeteit a tudós és követői számának ellenőrzése és mérése nem csupán a testsúly, hanem az összes jelenség a természetben előforduló és a lényege a harmónia uralkodott a világ, a lélek a kozmoszban.
Leírja a régi módszerek és a modern számítógépes technikákkal gyors véve, igyekeztem megmutatni, hogy a múltban és a jövőben, anélkül, hogy a matematika, a tudomány által létrehozott emberi elme nem képes.
„Ki vesz részt a matematika, hogy már korán, ő fejleszti a figyelmet, a vonatok az agy, akarata hozza kitartás és kitartás.” (A.Markushevich)