Összegzés kiszámítása koordinátáit súlypontja síkidom
- a súlypont koordinátáit.
Legyen egy síkban Oxy adott anyag pontrendszer
P 1 (x 1, y 1); P 2 (x 2, y 2);. P n (x n, y n)
c tömegek m 1, m 2, m n m 3 ..
Készítmények X i M i és y i M i nevezzük statikus pillanatok tömegéhez képest m-i és az Oy tengelyek Ox.
Jelölje x c és y c koordinátáit a súlypont a rendszer. Ezután a koordinátáit a súlypont a leírt anyag rendszer által meghatározott képletek:
Ezek a képletek meghatározásánál használt a súlypontok, különböző formájú és szervekkel.
- Súlypontja síkidom.
Legyen ez a szám által határolt vonalak y = f 1 (x), y = f 2 (x), X = A, X = b, egy lapos anyagdarab. Felületi sűrűsége, azaz az egységnyi felület, feltételezzük, hogy állandó és egyenlő delta minden részére az ábra.
Azt ossza ez a szám egyenes x = a, x = x 1 x = x n = b csíkokra szélessége 1 δ x, δ x δ x 2. n. A tömege egyes szalagok egyenlő a termék a maga területen sűrűségben δ. Ha minden szalag helyettesíti a téglalap (1. ábra) egy bázissal δ x i, és a magassága f 2 (ξ) -f 1 (ξ), ahol ξ. a csík megközelítőleg egyenlő a tömeg
Körülbelül a súlypont a csík lesz a központja a megfelelő négyszög:
Most cseréje minden szalag pontja az anyag, a tömege, amely egyenlő a tömeg a mindenkori szalag és koncentrálódik a súlypont a szalag, találunk egy közelítő értéke a tömegközéppontja a teljes ábra:
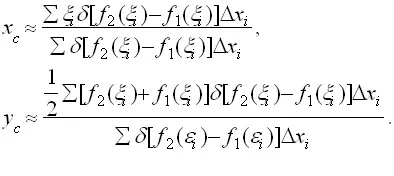
Átadás a határértéket. Kapunk pontos koordinátáit a súlypont az ábra:
Ezek a képletek érvényesek bármely homogén (vagyis van egy állandó sűrűségű minden ponton) síkidom. Mint látható, a tömegközéppontja helyzetben nem függ a sűrűsége δ ábra (a folyamat számítási δ csökkent).
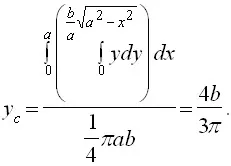
Keresse meg a koordinátáit az ív súlypontja felsővezeték.
1Tak a görbe szimmetrikus tengely körül Oy, annak súlypontja a tengely Oy, azaz X c = 0. Meg kell még talált. Aztán ott van az ív hossza
Használata tétel Goulden megtalálják a koordinátákat a súlypont egy negyed
.
Ha forog a negyed kör tengelye körül Ox megkapjuk a félgömb, amelynek térfogata megegyezik
Szerint a második tétel Goulden, itt egy negyed súlypontú a szimmetria tengelye, azaz a Azt a felezővonal a koordináta szöge, ezért