Physicexperts, Laplace képletű

Laplace formula

Tekintsük a folyadék felszínén, alapján néhány lapos kontúr. Ha a folyadék felület nem sík, a vágy, hogy csökkentse azt eredményezi nyomás képest további megy folyadék egy sík felületre. Abban az esetben, egy konvex felülete további nyomást pozitív, abban az esetben egy konkáv felület - negatív. Az utóbbi esetben, a felületi réteg célja zsugorodó, nyúlik folyadék.

Nagysága a további nyomást kell nyilvánvalóan növeli a növekvő felületi feszültség # 945; és a görbület felületet. Kiszámítjuk további nyomást a gömb alakú a folyadék felszínével. Ehhez rassechom gömb alakú csepp folyadék egy diametrális síkon a két félteke (ábra. 5).

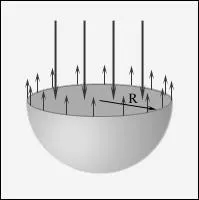
Keresztmetszete egy gömb alakú csepp folyadék.

Mivel a felületi feszültség a két félteke vonzzák egymást erővel egyenlő:

Ez az erő prések össze a két agyfélteke az S felület = πR2 és így okozza további nyomást:

# 8710; p = F / S = (2πR # 945;) / πR2 = 2 # 945; / R (4)

A görbület a gömb alakú felület mindenütt ugyanaz, és meghatározzuk gömb sugara R. Nyilvánvaló, hogy a kisebb R, annál nagyobb a görbülete egy gömb alakú felület. Egy tetszőleges felületi görbületét általában az jellemzi, úgynevezett átlagos görbület, amely eltérhet a különböző pontokat a felületen.

Az átlagos görbület által meghatározott görbületi normál szakaszok. A normális része a felület egy pontjának nevezzük metszésvonala ez a felület egy sík, amely átmegy a felületre merőleges ponton vizsgálják. Egy gömb, minden normális rész egy R sugarú kör (R-sugár gömb). Az érték H = 1 / R ad görbületi szférában. Általában a különböző keresztmetszetek áthúzzák ugyanazon a ponton különböző görbületű. A geometriában ha bebizonyosodik, hogy a félig összege inverz görbületi sugarak

bármely két egymásra merőleges normál szakaszok azonos értékű. Ez az érték az átlagos görbület ezen a ponton.

A sugarak R1 és R2 jelentése az (5) - algebrai értéket. Ha a görbületi középpontja a normál szakasz alatt található ez a felület megfelelő görbületi sugara pozitív, ha a görbületi középpont feküdt a felszínen, a görbületi sugár negatív.

Egy gömb, R1 = R2 = R, úgy, hogy, összhangban (5) H = 1 / R. Cseréje a (4) 1 / R H, azt találjuk, hogy

Laplace bebizonyította, hogy a (6) képletű érvényes minden felület alakja, ha érteni átlagos görbülete H a felszíni ezen a ponton, amely alatt további nyomást meghatározzuk. Behelyettesítve a (6), expressziója (5), hogy az átlagos görbület, megkapjuk a kifejezés a további nyomást egy tetszőleges felületre:

Ezt nevezik a Laplace képlet.

További nyomást (7) hatására a folyadék szintje változás a kapilláris, ezáltal néha kapilláris nyomás.

A létezése érintkezési szög vezet, amit a közelébe eső érfalat görbület a folyadék felszínén. A kapilláris vagy egy keskeny rés teljes felület közötti két íves fal. Ha a folyadék nedvesíti a falfelület konkáv alakú, amikor nem nedves - konvex (4. ábra). Ez a fajta görbe folyadék felszínén az úgynevezett meniszkusz.

Ha a kapilláris merítjük hogy az egyik vége a folyadék öntjük edénybe, majd egy görbe felület a kapilláris nyomás különbözni fog a nyomás a sík felület széles edényben összeggel # 8710; p, bizonyos képlet (7). Ennek eredményeként, nedvesítő a kapilláris folyadék szintje nem lesz magasabb, mint az edény, míg a nem-nedvesítő - az alábbiakban.

Ugrás oldalra 1 2