Pitagorasz-tétel, háromszög

Pitagorasz-tétel a geometria nem kevésbé fontos, mint a szorzótábla számtani. A megoldás számos geometriai probléma (például a síkrajzi és szilárd geometria), csökken, hogy a használata a derékszögű háromszögek és ez a figyelemre méltó tétel.

Egy derékszögű háromszög, a tér a átfogója egyenlő a négyzetének összege a másik két oldala.

Sok különböző módon bizonyítani a Pitagorasz-tétel. Korlátozzuk magunkat, hogy csak az egyiket.

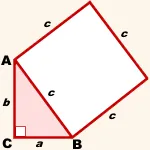
Hagyja, BC = a, AC = b, AB = c.

A átfogója AB össze egy négyzet oldala c.

A folytatása az oldalsó AC elhalasztja AF szegmens, AF = a,

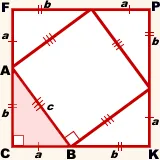
a kiterjesztése a része BC - szegmens BK, BK = b.

CF = AF + AC = a + b, CK = BC + BK = a + b, azaz CF = CK = a + b.

Pontokon keresztül F és K tölteni a párhuzamos egyenesek a lábát egy háromszög:

Négyszög CFPK - paralelogramma (definíció szerint).

És mivel ∠C = 90º és CF = CK, a CFPK - egy négyzet oldala a + b.

Mivel a terület a tér egyenlő a négyzetével oldalán,

Másrészt, CFPK terület összegével egyenlő területek négy derékszögű háromszögek lábakkal B és C egy négyzet oldala c.

területe egy négyzet oldala c egyenlő c².

Egyenlővé jobb oldalán képletek CFPK felületek:

Miután egyszerűsítés megkapjuk

QED.

Mivel a lába egy derékszögű háromszög leggyakrabban nevezik a és b. és a átfogója - mindkettő c, akkor a képlet Pitagorasz-tétel általában írt így: