ponderomotoros erők
Kondenzátor lemezek, ellentétes töltésű, vonzódnak egymáshoz.
Mechanikus ható erők töltött makroszkopikus testek nazyvayutponderomotornymi.
Kiszámoljuk az ponderomotoros ható erők a lemezeket egy sík kondenzátor. Van két lehetőség:
A kondenzátor feltöltődik, és leválasztják a feltöltött akkumulátor (ebben az esetben, a száma díjak a lemezeket állandó marad q = const).
Ha eltávolít egy kondenzátor lemez a másik munkát
ami miatt a potenciális energia rendszer növeli:
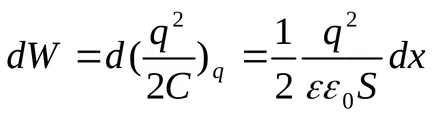
Ugyanakkor dA = dW. Egyenlővé jobb oldalán ezen kifejezések, megkapjuk
Ebben az esetben, ha különbséget a lemezek között nyilvánvalóvá vált x távolság.
A kondenzátor feltöltődik, de nem húzza ki az akkumulátor (ebben az esetben, amikor a mozgó egyik kondenzátor lemezek tartjuk állandó feszültség (U = const). Ebben az esetben, eltávolítására egyetlen lemezt a másik potenciális energia kondenzátor területen csökken, mivel van egy „szivárgás” töltés tányérok, így
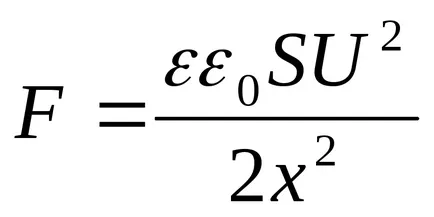
A kapott expressziós egybeesik a képlet
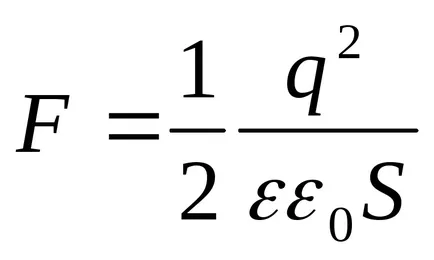
Field egységes. A térerősség a kondenzátor egyenlő
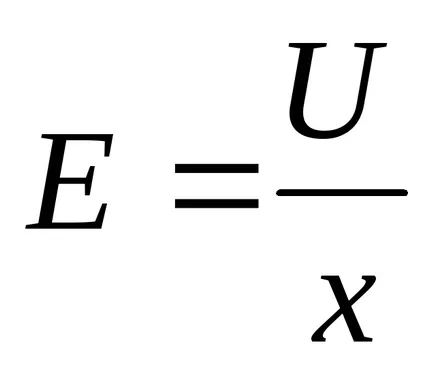
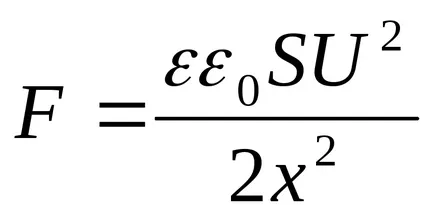
Ezek az erők hatnak nemcsak a tányéron. Mivel a lemez, viszont nyomja meg a szigetelő, közéjük helyezett és deformálódik, akkor a nyomás jön létre a dielektromos
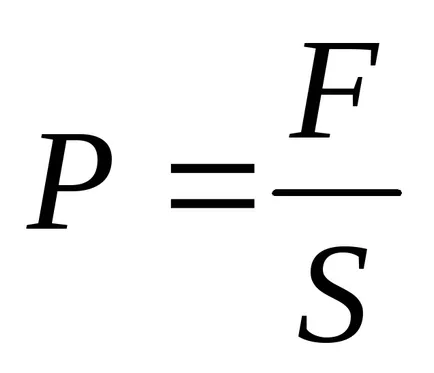
(S - terület minden egyes lemez).
Nyomás előforduló dielektromos valamint
Példák problémák megoldása
12. példa 5.K síkban levegő kondenzátor lemezeket alkalmaznak egy potenciális különbség 1,5 kV. Tér lemezek 150sm2i távolság van közöttük 5 mm. Miután leválasztotta a kondenzátort a feszültségforrást a teret az üveglapok között beillesztett (ε2 = 7) .Opredelite:
1) a potenciális különbség a lemezek közötti alkalmazása után a dielektromos; 2) A kondenzátor kapacitása előtt és után a szigetelő; 3) A felületi töltéssűrűség a lemezeken előtt és után a bevezetése a dielektrikum.
Tekintettel. U1 = 1,5 kV = 1,5 ∙ 10 3 V; S = 150cm 2 = 1,5 ∙ 10 -2 m 2; ε1 = 1; d = 5mm = 5 ∙ 10 -3 m.
Határozat. mert
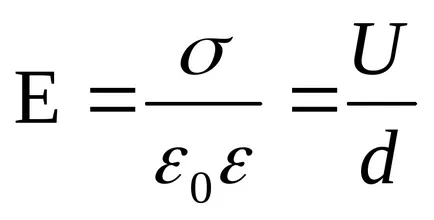
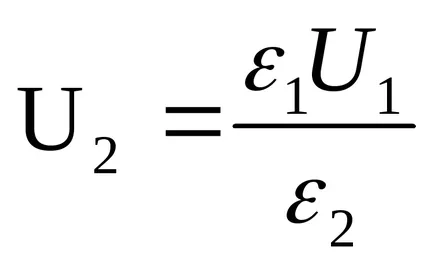
Kondenzátor kapacitása előtt és után bevezetése dielektromos
Bolt lemezeket miután leválasztják a feszültségforrás nem változik, azaz, q = const. Ezért a felületi töltéssűrűség a lemezeken előtt és után bevezetése dielektromos
Példa 12.7. A lemezek közötti hézag egy síkkondenzátor van töltve egy anizotrop dielektromos állandója ε változik, ami egy olyan irányban, amely merőleges a lineárisan felé lemezeket ε = α + βh a ε1do ε2, sőt ε2> ε1. A terület egyes obkladkiS közötti távolság nimid. Keresse meg a kondenzátor kapacitása.
Határozat. Dielektromos pronitsaemostε lineárisan változó. ε = α + βh ahol x mérjük az elektróda, amely konstans ε1. Tekintettel arra, hogy ε (0) = ε1. ε (d) = ε2. megkapjuk a függőség
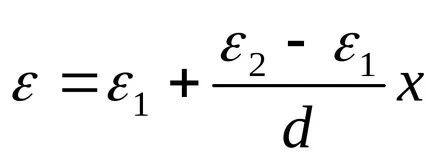
kondenzátor kapacitása egyenlő lesz
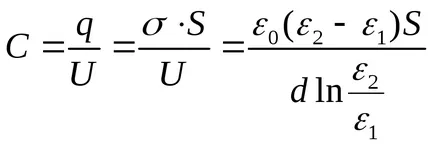
Példa 12.7. A lemezek között egy sík kondenzátor terhelt, a különbség potentsialovU. a lemezekkel párhuzamosan a két réteg dielektromos elhelyezett. A rétegeinek vastagsága, és a permittivitás dielektrikumok rendre ravnyd1, d2, ε1, ε2. Határozza meg a intenzitása elektrosztatikus mezők a dielektromos rétegekben.
Határozat. A feszültség a kondenzátor lemezeket, tekintettel arra, hogy a területen belül minden egyes dielektromos rétegek egyenletes,
Elektromos elmozdulás mindkét dielektrikumrétegekben ugyanúgy, így tudjuk felvenni
Tól kifejezések (1) és (2) nem találja a kívánt
Tól képletű (2) következik, hogy
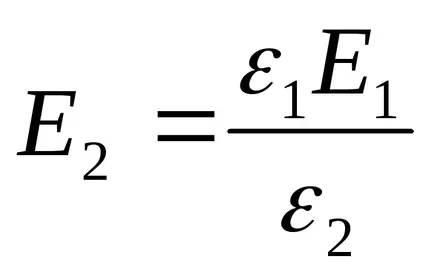
Példa 12.7. Area plastinSploskogo kondenzátor 100cm2. A tér a lemezek között tele van két réteg dielektromos szorosan - a csillám lemez (ε1 = 7) tolschinoyd1 = 3,5 mm, és a paraffin (ε2 = 2) tolschinoyd2 = 5 mm. Határozza meg a kondenzátor kapacitása ..
Határozat. kondenzátor kapacitása
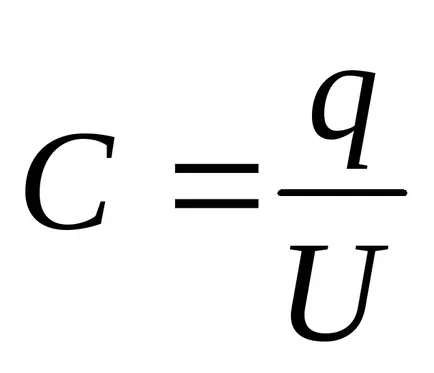
ahol = - kondenzátor töltésének lemezeken (- felületi töltéssűrűség a lemezeken); = - feszültségkülönbség lemezek, egyenlő a feszültség nagysága a dielektromos rétegek: U = U1 + U2. majd
Feszültségek U1 és U2 található a képletek
ahol E1 és E2 - intenzitású elektrosztatikus mezők az első és a második dielektromos réteg; D - elektromos elmozdulás dielektrikumokban (mindkét esetben azonos). Figyelembe véve, hogy
És adott képletű (2), a (1) kifejezés megtalálják a kívánt kondenzátor kapacitásához
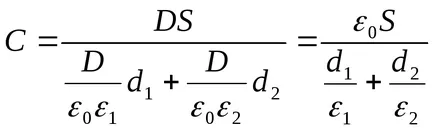
Határozat. A sorosan kapcsolt kondenzátorok díjat minden lemezek között azonos nagyságrendű, így
A kondenzátor feszültsége
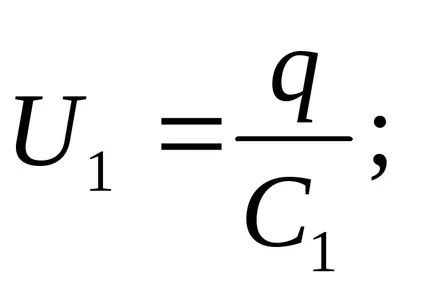
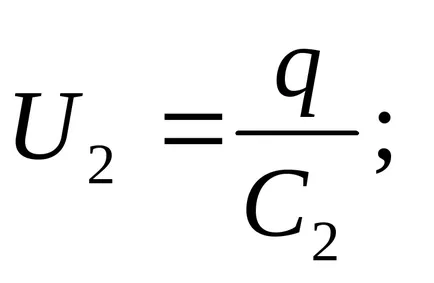
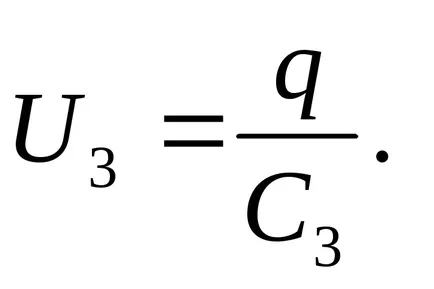
EMF összege a forrás feszültség az egyes sorba kapcsolt kondenzátorok:
Amikor csatlakozik foglalta reciprokokat a kapacitás az egyes kondenzátorok:
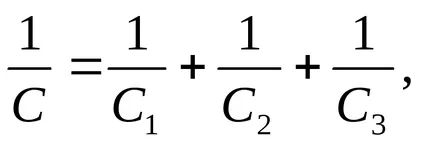
Amennyiben a kívánt kondenzátor kapacitása bank
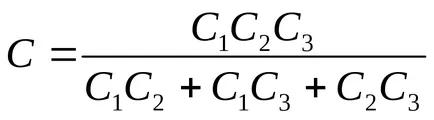
Példa 12.7. Két sík levegő kondenzátor az azonos kapacitás sorba vannak kapcsolva, és csatlakozik az EMF forrás. Hogyan és hányszor kell változtatni a felelős a kondenzátor, ha egyikük merítjük olaj dielektromos állandója ε = 2,2.
Határozat. Amikor a készüléket a kondenzátor díjak mindkét kondenzátorok egyenlő nagyságú. Bemerítés előtt a dielektromos (olajban), a töltés az egyes kondenzátor
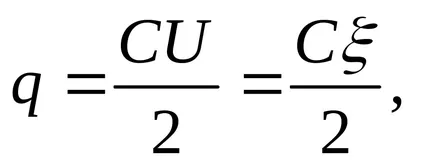
ahol ξ = U1 + U2 (sorosan kapcsolt kondenzátorok EMF forrás feszültség összegével egyenlő az egyes kondenzátorok).
Bemerítés után az egyik kondenzátorok a kondenzátor dielektrikum díjak ismét azonos, és rendre az első és második kondenzátorok
(Figyelembe véve, hogy ε1 = 1), ahol, ha figyelembe vesszük, hogy a ξ = U1 + U2. talál
Felosztása (2) által (1), hogy megtalálja a kívánt arányt
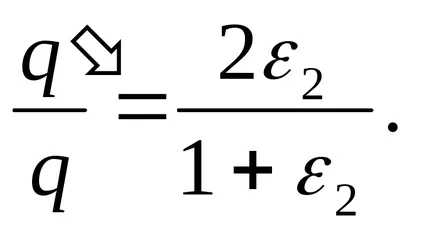
válaszolni:
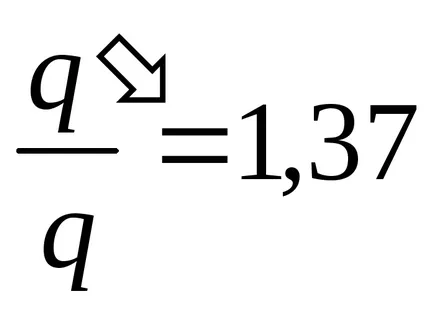
Példa 12.7. kondenzátorok A kondenzátorok C kapcsolódnak össze a megjelölt ris.a. kapacitás meghatározását Sobschetogo kapcsolatot kondenzátorok.
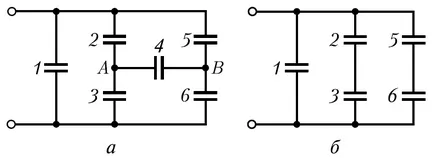
Ez vázlatosan három párhuzamos ág, melyek közül kettő tartalmazhat két sorozatú kondenzátorok benne
Példa 12.7.Plosky légi kapacitás C1 kondenzátor fel van töltve, hogy 4PF = eltérés potentsialovU1 = 100V. Miután leválasztotta a kondenzátort a feszültségforrás közötti távolság kondenzátor lemezeket két alkalommal növekszik. Adjuk meg: 1) a különbség potentsialovU2na kondenzátor lemezeket után razdvizheniya; 2) a munkát a külső erők razdvizheniya lemezeken.
Határozat. A töltés a kondenzátor lemezeket, amikor le van választva az feszültségforrás nem változik, azaz, Q = const. ezért
ahol a C2 és U2 - és a tartály, illetve a potenciális különbség az egész kondenzátor lemezeket után kenhető.
Tekintettel arra, hogy a kapacitás a lakás kondenzátor
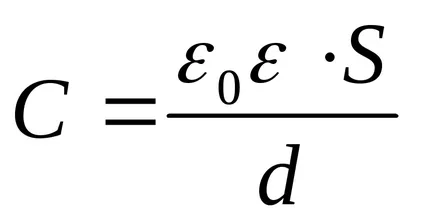
Miután leválasztotta a kondenzátort a feszültségforrás rendszer két töltött lemezek tekinthetők zárt, amelyre a törvény az energiamegmaradás: A munka a külső erők egyenlő a rendszer energiája változás
ahol a képletben W1 és W2 - rendre kondenzátor energia területén a kezdeti és a végső állapotok.
feltéve, hogy
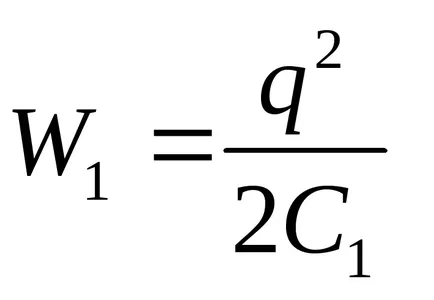
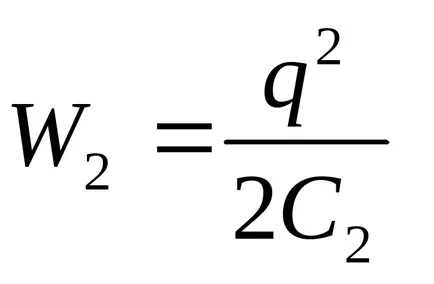
Példa 12.7.Sploshnoy labdát dielektromos radiusomR = 5 cm egyenletesen töltött ömlesztett sűrűségű ρ = 5nKl / m3. Határozzuk meg az energia elektrosztatikus tér, zárt körülvevő térbe a labdát.
Határozat. Field töltött labda gömbszimmetrikus, így a tér töltés sűrűsége azonos minden ponton található egyenlő távolságra a központtól a labdát.
E
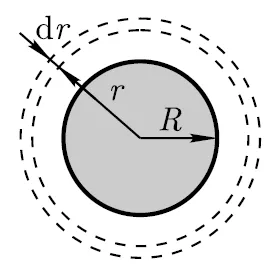
ahol dV = 4πr 2 Dr (r - a sugara a gömb alakú elemi réteget; dr - vastagsága);
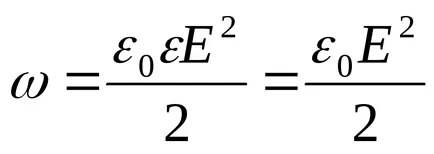
Intenzitás E találni Gauss tétel területén vákuumban, és egy zárt felület mentálisan válasszuk gömb sugara r (lásd. Ábra). Ebben az esetben a teljes belső felülete el töltés ítéljük, hogy létrehozza a szóban forgó területet, és a Gauss-tétel
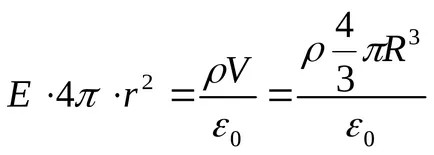
Behelyettesítve ezeket a kifejezéseket a általános képletű (1), megkapjuk
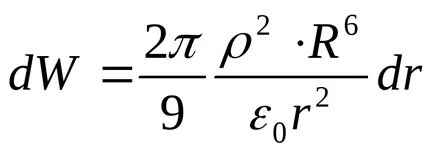
Energia, amely a környező tér labda,
Válasz. W = 6,16 ∙ 10 -13 J.
Példa 12.7.Ploskomu kondenzátor területe obkladokSi térköz ℓ közölt zaryadq. ami után a kondenzátor lekapcsolódik a feszültségforrás. Határozzuk meg az erő prityazheniyaFmezhdu kondenzátor lemezeket, ha a dielektromos állandója a közeg a lemezek között egyenlő ε.
Határozat. A töltés a kondenzátor lemezeket, amikor le van választva az feszültségforrás nem változik, azaz, q = const. Tegyük fel, hogy az az erő a vonzás F közötti távolság a kondenzátor lemezeket változott d ℓ. Ezután az F erő működik
A törvény szerint az energiamegmaradás, ez a munka egyenlő az energiaveszteség a kondenzátor, azaz
ahol alapján kifejezések (1) és (2), megkapjuk
Behelyettesítve a kifejezés az energia a feltöltött kondenzátor
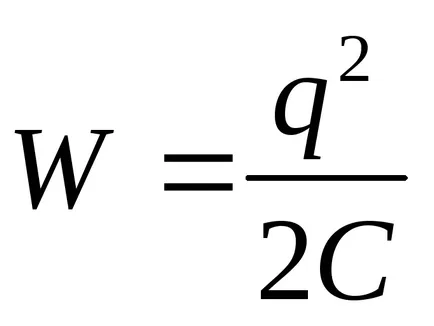
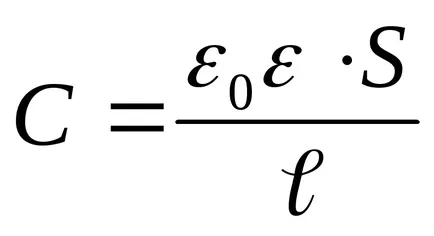
Behelyettesítve a (3) Az energiatartalmat (4) és a teljesítő differenciálódás, megtaláljuk a szükséges húzóerő a kapacitás lemezek között
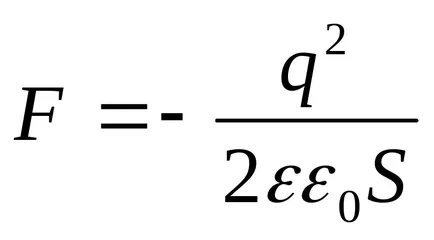
ahol a „-” jel azt jelzi, hogy az F erő a vonzóerő.
Példa 12.7.Plosky kondenzátor területen obkladokSi térköz ℓ csatlakozik az állandó napryazheniyaU. Határozzuk meg az erő prityazheniyaFmezhdu kondenzátor lemezeket, ha a dielektromos állandója a közeg a lemezek között egyenlő ε.
Határozat. Szerint probléma állapota a kondenzátor lemezeket tartjuk állandó feszültség, azaz U = const. Tegyük fel, hogy az az erő a vonzás F közötti távolság a kondenzátor lemezeket változott dl. Ezután az F erő működik
A törvény szerint az energiamegmaradás, a munka ebben az esetben megy, hogy növelje a kondenzátor teljesítmény (hasonlítsuk össze a korábbi gyakorlat), azaz
ahol alapján kifejezések (1) és (2), megkapjuk
Behelyettesítve a kifejezés az energia a kondenzátor
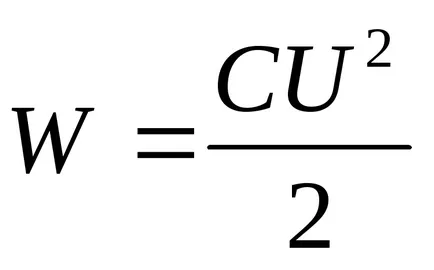
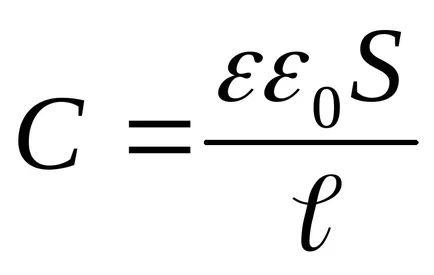
Behelyettesítve a (3) Az energiatartalmat (4) és a teljesítő differenciálódás, megtaláljuk a szükséges húzóerő a kapacitás lemezek között
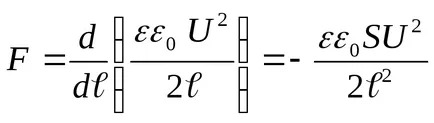
ahol a „-” jel azt jelzi, hogy az F erő a vonzóerő.