Pontos differenciálegyenletek, példák, oldatok
A bal oldalán a differenciálegyenletek formájában néha teljes különbségek az egyes funkciókat. Ha a visszaállítási funkciót a teljes eltérés, az általános szerves A differenciálegyenlet található. Ebben a cikkben, leírjuk egy eljárás helyreállítása funkciót a teljes eltérés, az elméleti példákat nyújt és problémák részletes megoldásokat.
A bal oldalon a differenciálegyenlet a teljes eltérés egy függvény U (x, y) = 0. Ha a feltétel.
Mivel a teljes eltérés a függvény U (x, y) = 0, ha a feltétel lehet mondani, hogy. Következésképpen ,.
Az első egyenlet van. A funkció használatával is megtalálható a második egyenletet:

Tehát azt tapasztaltuk, a kívánt funkciót U (x, y) = 0.
Keresse az általános megoldás a differenciálegyenlet.
Ebben a példában. A feltétel teljesül, például a
Ezért, a bal oldalán az eredeti differenciálegyenlet teljes eltérés egy függvény U (x, y) = 0. A probléma csökken megtalálása ezt a funkciót.
Mivel van egy teljes eltérés egy függvény U (x, y) = 0. Ekkor. Integrálható első egyenlet x és y differenciálható eredményt. Másrészt, van a második egyenletből. ezért
ahol C - egy tetszőleges konstans.
Így a teljes integrál az egyenlet az eredeti.
Van egy másik módszer megtalálására a teljes eltérés ellátásához. Ez abban áll, figyelembe véve a vonalintegrál egy rögzített pont (X0. Y0), hogy a pont a változó koordinátái (x, y). . Ebben az esetben az az integrál értékét nem függ az integráció útján. Kényelmes, hogy mert így a integrálására a szaggatott vonal, a linkeket, amelyek párhuzamosak a koordináta tengelyekkel.
Tekintsük a következő példát.
Keresse az általános megoldás a differenciálegyenlet.
Ellenőrizze állapot:
Így a bal oldalon a differenciálegyenlet a teljes eltérés egy függvény U (x, y) = 0. találni ezt a funkciót, hogy kiszámítjuk a vonal integráns ponttól (1, 1) a (x, y). Mivel az integráció útját veszi vonallánc: egy első része lejtős menetben egy egyenes vonal y = 1 a pont (1, 1) a (x, 1). egy második útvonalon részét veszi egyenes vonalban a pont (x, 1) az (x, y).
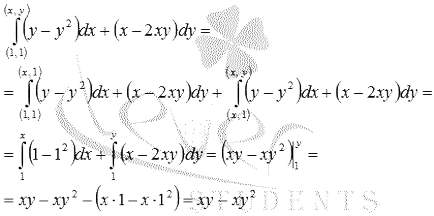
Így, az általános megoldás a differenciálegyenlet formájában.