Prism és egy doboz
Face a doboz, nincs közös csúcsok nevezzük szemben. [4, 301]
Paralelepipedon, amelynek oldalsó szélei merőlegesek a alapsíkkal, az úgynevezett közvetlen paralelepipedon. Ő az oldalfelületeket a téglalapok és paralelogramma alapja. Ha minden az arcát a doboz - téglalap, ez az úgynevezett hasáb alakú. A hossza három széle, amely meghosszabbítja egy vertex, úgynevezett méretei egy derékszögű paralelepipedon.
Kocka alakú, mind a három dimenziója egyenlő hívják kocka. Az arány közötti különféle paralelepipedon megadott az alábbi reakcióvázlat: [2, 115]
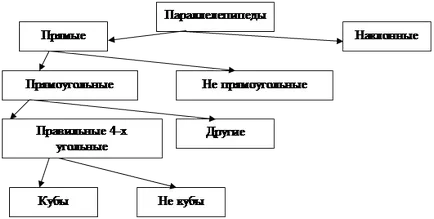
1), és az ellentétes felülete párhuzamos;
2) mind a négy átló metszéspontja egy ponton, és ossza félbe.
1) Tekintsük bármely két szemközti felületei a doboz, például,
kocka mérete: D = a√3.
A az alap kerületét: P = 4a.
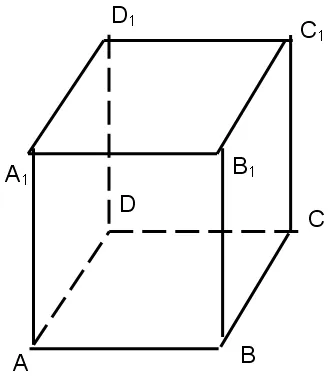
2. Az alapja sorban a prizma egy egyenlő szárú háromszög, amelyben a magassága megegyezik a szubsztrátum tartott 8 cm-es. A magassága a prizma egyenlő 12cm. Megtalálja a teljes felülete a prizma, ha az oldalsó, amely tartalmazza az alap a háromszög - téren.
A felület a prizma egyenlő lesz az összege területek bázisok, és a területek összegét az oldalsó felületek, azaz a
- a prizma bázis,
- az oldalsó felület, amely egy bázist,
- oldalán felülete, amely a része egy egyenlő szárú háromszög. (Ezek, mint a bázis oldalán vannak következtében egyenlő szárú háromszög, és a második oldalon vannak prizma magassága)
Mivel az oldallapok tartalmazó az alapja a háromszög, négyzet, az alap a háromszög is egyenlő 12 cm. (A háromszög alapja az oldalfelületek egyidejűleg).
Így, ismerve a magasság és a bázis egy egyenlő szárú háromszög, akkor megtalálja és egyéb szempontok a tér:
A lábak, rendre (megvan a magasság, amely egy szabályos háromszög, mind a medián
, minden a láb formáját derékszögű háromszög) a Pitagorasz-tétel:
,
3. A jobb négyszögletes hasáb lábnyom 144
, és magassága 14 cm. Keresse meg a diagonális prizma.
Helyes négyszög - egy négyzet.
Ennek megfelelően, a bázis oldalán lesz egyenlő
Amennyiben átlós jobb derékszögű hasáb bázis egyenlő
Átlós prizma formák helyes átlós alapja és magassága a prizma-hegyesszögű háromszög. Ennek megfelelően a Pitagorasz-tétel átlós előre meghatározott rendszeres négyszögű hasáb lesz egyenlő:
4. Vegyünk egy szabályos téglalap alapú hasáb
, átlós részén, amely - egy négyzet. fölött
és a középső bordák AB és BC tartotta a gépet. Keresse meg a területet a kapott keresztmetszete, ha
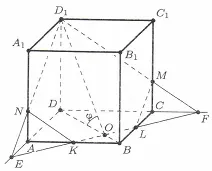
Épületrész az ábrán látható, ahol a K és L - felezőpontja az AB oldalára és BC a prizma bázis, E és F - a metszéspont a vonal KL, sorrendben, a kiterjesztések oldalainak DA és DC. Szakasz egy ötszög
ahol megtalálható a környéken. Mozhnosnachala számítani a területen háromszögek
majd kivonjuk kétszer a második terület (háromszögek, mint az első háromszög
egyenlő). Azonban ebben az esetben könnyebb használni a képlet:
síkjával prizma bázis egy ötszög
, Találunk egy olyan terület, kivonva a terület a négyzet
VKL a háromszög területe:
Legyen BD bázis átlós keresztezi KL szegmens azon a ponton O. Mivel
(Szerint a három merőlegesek tétel), majd a
- lineáris diéderes szög KL.
Derékszögű háromszög
Pitagorasz-tétel, van:
5. Dana jobb hasáb:
,
. Keresse meg a magassága a prizmát.
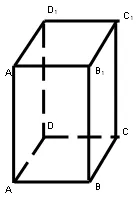
P = a az alap kerületét 8 cm.
6. Az ok a doboz téren. Az egyik felső alap csúcsai egyenlő távolságra minden csúcsa az alsó bázis és a parttól b ettől a bázist. Az alsó oldalon egy. Keresse meg a teljes felületén a doboz.
- egy doboz a bázisok
,
és az oldalsó szélek
, És ABCD - tér oldalán a. csúcs
egyenlő távolságra csúcsokat az A, B, C és D, valamint a távolság a vertex
a bázis síkban ABCD egyenlő b. hiszen a lényeg
egyenlő távolságra a csúcsai a ABCD négyzet, ez fekszik a síkra merőleges ABCD középpontján átmenő O a tér. Merőleges csökkent O pont a BC oldalán, áthalad a közepén M. A tétel a három merőlegesek
. Derékszögű háromszög
.
Ha S - a teljes felület a doboz
.
7. Bizonyítsuk be, hogy ha a keresztmetszet síkjában téglatest egy sokszög több oldalról háromnál nagyobb, akkor ez a sokszög párhuzamos oldala.
A paralelepipedon három pár párhuzamos arcok. Ha a sík metszi több mint három arcot, akkor legalább két oldalú sokszög keresztmetszetű vannak ellentétes oldalán a doboz. A tétel a kereszteződés két párhuzamos síkban a harmadik, a két oldal párhuzamos.
8. téglatest
a vonal ABCD - oldalú négyzet 5, egy borda
5 is, és ez a borda formák, a széleket AB és AD szögek
.
egyenlő egymással, ez azt jelenti, hogy a magasság
ez a piramis középpontján átmegy a kör körülírt a bázis ABD. valamint közepén átfogója BD, azaz - ABD derékszögű háromszög, az O pont ABCD négyzet középpontja. Derékszögű háromszög
egyenlő távolságra C és D csúcsok, tehát ez a merőleges vetülete K a talaj síkja ABCD is egyenlő távolságra a C és D, és így fekszik a merőleges a CD szakaszt. mint
||
=
- egy téglalap, így OK =
= 5. KO továbbra is vágni, hogy a kereszteződés az AB szakasz ponton M. Ezután M - felezőpontja AB és MK = MO + OK =
. MKB és szögben álló háromszögek
9. A szélén AD és átlós
vesszük, M és N pontok, sőt vonal MN párhuzamos
és AM: AD = 1: 5. megtalálni az arány
.
Legyen P - a központ a ABCD paralelogramma. sík
- Prism bázisokkal
úgynevezett N - szén prizma.
- Merőlegesen húzott bármely pontján egy bázis másik alapsík úgynevezett magassága a prizma.
Ha az oldalsó élei merőlegesek a bázisok a prizma, a prizma az úgynevezett közvetlen egyébként - ferde. A magasság az egyenes hasáb oldalirányú szélét.
- Prism nevezzük szabályos, ha az alap - szabályos sokszög.
Ha az alap prizma egy paralelogramma, ez az úgynevezett téglatest. Minden részletét a doboz - paralelogramma.
- Face a doboz, nincs közös csúcsok nevezzük szemben.
- Paralelepipedon, amelynek oldalsó szélei merőlegesek a alapsíkkal, az úgynevezett közvetlen paralelepipedon.
- A dobozban minden oldala nézzen a téglalapok és paralelogramma alapja. Ha minden az arcát a doboz - téglalap, ez az úgynevezett hasáb alakú.
- A hossza három széle, amely meghosszabbítja egy vertex, úgynevezett méretei egy derékszögű paralelepipedon.
- Kocka alakú, mind a három dimenziója egyenlő hívják kocka.