QS várakozással (queue)
Ahogy teljesítménymutatók QS várakozással mellett a már ismert teljesítmény - abszolút és relatív sávszélesség, a kudarc valószínűsége, az átlagos elfoglalt csatornák (többcsatornás rendszer) is figyelembe kell venni a következőket:
1) - az átlagos megrendelések száma a rendszerben;
2) - átlagos tartózkodási ideje az alkalmazást a rendszer;
3) - az átlagos kérelmek száma sorban (sorhossz);
4) - az átlagos időt töltött a bejelentési szakaszban;
5) - annak a valószínűsége, hogy a csatorna foglalt (csatorna kihasználtság foka).
Egycsatornás rendszert végtelen sorban
Van egy egycsatornás QS egy sorban, amelyen nincs korlátozás (vagy a hossza a sorban nincs időtúllépés). Takarmány beérkezett a QS egy intenzitású, és a fluxus karbantartási - intenzitása. Meg kell találni a határ valószínűsége feltételek és teljesítménymutatók SMO.
A rendszer lehet az egyik államok szerinti szervezetek száma a QS: - a csatorna szabad; - csatorna foglalt (szolgáltató alkalmazás), nincs sorban; - a csatorna foglalt, egy kérelem sorban áll; - a csatorna foglalt, kérések a sorban, stb
Count SMO állapotot ábrán látható. 8.
Ez a folyamat a születés és a halál, hanem egy végtelen sok állapot, amelyben az áramlás a kérelmek egyenlő az intenzitás és az áramlási sebesség karbantartás.
Mielőtt írni a képlet marginális valószínűségek, akkor biztosnak kell lennie abban a létezésükről, mert ha az idő minden növelheti a végtelenségig. Bizonyított, hogy ha, azaz, az átlagos száma a bejövő kérések kisebb, mint az átlagos száma kiszolgált kérések (időegység alatt), a marginális valószínűségek léteznek. Ha minden nő a végtelenségig.
Annak megállapításához, a marginális valószínűségi állapotok használja a képlet (16), (17) a születés és halál folyamata (itt feltételezzük, bizonyos mértékű hiánya a szigor, mint korábban, ezek a képletek alapján készültek esetén véges sok állapot a rendszer). kapjuk:
8. példa A kikötő dokk kirakodás hajókat. Az áramlási sebesség 0,4 hajók (hajók naponta). Átlagos ideje kirakodó hajó 2 nap. Feltételezzük, hogy a sorban lehet korlátlan hosszúságú. Keresse teljesítménymutatók fekhelyen, valamint annak a valószínűsége, hogy a várható kibocsátás nem több, mint 2 hajó.
Határozat. Van. Mivel, majd kapcsolja be a leterhelő nem növelhető a végtelenségig, és korlátozza a valószínűsége van. Megtalálni őket.
Annak a valószínűsége, hogy a mólón szabadon (33), és annak a valószínűsége, hogy foglalt. A (34) képletű a valószínűsége, hogy a horgonyzó 1, 2, 3 az edény (azaz váró kirakodás 0, 1, 2 hajó) egyenlő
Annak a valószínűsége, hogy a várható kibocsátás nem több, mint 2 hajó
Képlet (40), az átlagos hajók száma váró kirakodás, az átlagos várakozási idő a mentesítés a képlet (42) (éjszakai).
A képlet szerint (36) az átlagos száma horgonyzó hajók (nap) (vagy egyszerűbb (37) (nap), és az átlagos tartózkodási idő a hajó a Pier amelyet a képlet (41) (nap).
Nyilvánvaló, hogy a hatékonyság a kirakodás hajók alacsony. Javítani szükséges csökkenteni az átlagos idő a kirakodás a hajó vagy számának növelése kikötőhelyek.
Többcsatornás QS korlátlan sorban
Tekintsük meg a problémát. Van egy n-csatornás QS korlátlan sorban. Takarmány beérkezett a QS egy intenzitású, és a fluxus karbantartási - intenzitása. Meg kell találni a határ valószínűségi állapot QS és teljesítményét annak hatékonyságát.
A rendszer lehet az egyik államok számozása a szervezetek száma, a CMO: - a rendszernek nincs ajánlatok (minden csatorna ingyenes); - egy csatorna foglalt, a fennmaradó szabad; - két csatorna foglalt, mások szabadon; - csatorna foglalt, mások szabadon; - minden csatorna foglalt (no queue); - foglalt összes csatornát a sorban egy alkalmazás; - minden csatorna foglalt, megrendeléseik sorok stb
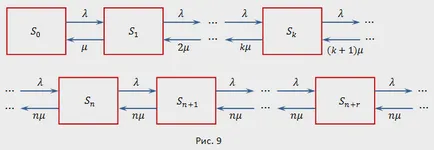
Gróf rendszer állapotát ábrán látható. 9. Tudomásul vesszük, hogy ellentétben a korábbi QS intenzitás fluxus karbantartás (átviszi a rendszer egyik állapotból a másikba, jobbra) nem marad állandó, hanem az alkalmazások száma a QS 0-ról a nagysága, hogy már illetve a szolgáltatók számát csatornák növekszik. Ha a kérelmek száma a QS-nél nagyobb az áramlási sebesség tárolt szolgáltatási egyenlő.
Meg lehet mutatni, hogy a korlátozó valószínűségek léteznek. Ha minden nő a végtelenségig. A képletek (16) és (17) a születés és halál folyamat, mi állíthatjuk elő az alábbi képletet a marginális valószínűségek államok n-csatornás QS korlátlan sorban
Az átlagos tartózkodási idő a kérelem várakozási sor, és az átlagos tartózkodási idő az alkalmazás rendszer, mint korábban, által adott Kis (42) és (41).
Megjegyzés. Mert QS korlátlan sorban bármilyen alkalmazás, amely jött, akkor gondoskodni kell, azaz a valószínűsége a kudarc, a relatív sávszélesség, és a sávszélesség is egyenlő az abszolút intenzitása a beérkező áramlását kérések, azaz .
9. példa a szupermarketben számítani a csomópont belép az áramlás az ügyfelek az intenzitás az emberek. óránként. Az átlagos hossza szolgáltatás vezérlő-Teller egy vevő min. meghatározni:
a. A minimális számú pénztárosok, vezérlők, amely nem sorba fog nőni a végtelenségig, és megfelelő karbantartás jellemzőket.
a. Annak a valószínűsége, hogy a vonal nem lesz több, mint három vásárlók.
Határozat. a. A feltétel (1 / óra) (1 / min.). A (24) képletű. Sor nem fog növekedni a végtelenségig, feltéve, hogy a \ rho = 2, \! 7 "src =" http://bourabai.ru/cm/waiting_sys/mathtex(82).gif „>. Így a minimális számát vezérlők-pénztárosok.
Találunk a jellemzői a szolgáltatás a CFR.
Annak a valószínűsége, hogy a csomópont nem számítás vásárlók, a képlet (45)
azaz átlagosan 2,5% az idő vezérlők pénztárosok lesz tétlen.
Annak a valószínűsége, hogy egy csomópont számítási bekapcsol (48)
Az átlagos ügyfelek száma a sorban, a (50)
Az átlagos várakozási idő a sorban, és jegyet egyébként rendre (képlet alapján (42) és (41)):
Szerint a második kiviteli alak van két egycsatornás QS (két speciális ablak); minden egyes bejövő áramot kérelmek intenzitással. Mint korábban, a korlátozó valószínűségek léteznek. Képlet alapján (40) és (36), (42), (41)
Tehát a második kiviteli és a megnövekedett hossza a sorban, és az átlagos várakozási idő, és általában a jegyvásárlás. Ez a különbség azzal a ténnyel magyarázható, hogy az első kiviteli (kétcsatornás SMO) kevesebb, mint az átlagos százalékos aránya tétlen az egyik szavazatszámláló, ha nem foglalt szervizelése utas vásárol jegyet a lényeg, ő tehet szolgáltatás utas, aki vásárol jegyet egy pont, és fordítva . Egy második megvalósítási mód, nincs ilyen felcserélhetőség.
Látható, hogy a közbeeső időben nőtt több mint 2-szerese a jegyvásárlás a második kiviteli alakban. Ez a jelentős növekedés annak a ténynek köszönhető, hogy a CFR működik, maximális kapacitás: csak kis mértékben növeli az átlagos szolgálati idő, azaz csökken, és meghaladja az 1, azaz a minden elkezd nőni a végtelenségig.
b. Fent azt találtuk, hogy megfelelően az első kiviteli jegykiadó átlagosan egy utas kiszolgálási idő (perc) átlagos ideje a jegyvásárlás összeg (min). A feltevés a második kiviteli alak az eladás, vagy figyelembe véve (36) és (41).
Feltételezve azt kapjuk, ahol megtalálja, vagy (m).
Így az átlagos idő a vásárlás a második kiviteli alak ticketing csökkenthető, ha az átlagos szolgálati idő egy utas csökken több, mint 0,17 m, vagy több, mint 8,5%.
QS Korlátozott Sorba
QS korlátozott várakozási eltérnek a fenti csak abban a kérelmek száma a sorban korlátozott (nem haladhat meg egy bizonyos előre). Ha az új alkalmazás egy időben, amikor minden ülés foglalt a sorban, akkor elhagyja a SMO unserviced, azaz elutasítják.
Nyilvánvaló, hogy a számítási korlátozása valószínűségek az államok és a hatékonyság ilyen SMO lehet használni ugyanazt a megközelítést, mint fent, azzal a különbséggel, hogy összefoglalják nem kell végtelen progresszió (ahogy tettük a levezetése (33) képletű), és a végső . A megfelelő képleteket a táblázatban. 3.
Az átlagos tartózkodási idő a sorban, és az alkalmazás a rendszerben, ahogy azt korábban formula határozza meg Kis (44) és (43).
11. példa 8 A hipotézis keresési teljesítmény mutatók mólón. Köztudott, hogy a beérkező hajó elhagyja a dokk (nem kirakodott), ha a kirakodás sorban többet ér, mint 3 hajó.
Határozat. Azzal a feltétellel. Mi megadott képlet segítségével a táblázat második oszlopában. 3.
Annak a valószínűsége, hogy a mólón ingyenes,
Annak a valószínűsége, hogy a beérkező hajó elhagyja a dokk kirakodása nélkül:
Átlagos száma horgonyzó hajók, valamint az átlagos tartózkodási idő a hajó a móló (41):
QS korlátozott várakozási idő
A gyakorlatban gyakran QS úgynevezett „türelmetlen” alkalmazások. Ilyen alkalmazások például hagyja el a sorban, ha a várakozási idő meghalad egy bizonyos összeget. Különösen ez a fajta alkalmazás felmerülő különböző technológiai rendszerek késleltetheti a szolgáltatás elvesztését eredményezheti a minőségi termékek, a működési rendszerek, amikor sürgős üzenetek elveszti az értékét (vagy értelme), ha azok nem a szolgáltatás egy bizonyos időben.
Az ilyen rendszerekben azt feltételezzük, egyszerű matematikai modellt, amely az alkalmazás lehet a sorban a véletlenszerű időben elosztott exponenciálisan bizonyos paraméterrel, Akkor feltételesen feltételezni, hogy minden alkalmazás, sorban állni a szolgáltatás, akkor hagyja a rendszert intenzitással.
Vonatkozó eredményességi mutatókat QS korlátozott ideig kapunk alapján kapott eredmények a folyamat a születés és halál.
Összefoglalva, azt látjuk, hogy a gyakorlatban gyakran előfordul zárt rendszer karbantartása. ahol a bejövő áramlás kérelmek alapvetően attól függ, az állam az SMO. Példaként egy olyan helyzetben, ahol javítási lehetőség a területen működésének néhány az autók: egyértelmű, hogy minél több gép egy állapotban, annál kevésbé továbbra is használnak, és minél alacsonyabb a folyamat intenzitása az új belépők a javítás gép. Zárt QS karakterisztika egy korlátozott számú forráskódú alkalmazások minden forrás „blokkolt” a szolgálati idő az alkalmazás (vagyis nem ad ki új kérelmek). Az ilyen rendszerekben a véges sok állapot QS marginális valószínűséggel meglesz az értéket az áramlási sebesség alkalmazásokat és szolgáltatásokat. Ezeket ki lehet számítani, ha visszatér a folyamat a születés és halál.
Tudtad, hogy az időskálán - egy szám, amely megadja az időtartama a szimulációs modell egy időegység, az újraszámított másodpercben, valós időben Csillagászati másodperc, amikor a modell.
Hírek Fórum
Knights-éter elmélet