Rastyazhenie_szhatie diákok
Tension (tömörítés) a rúd úgynevezett stressz állapot, amelyben annak bármely keresztmetszetének valamennyi belső erők egyenletesen oszlanak el az egész szakasz, feltéve, hogy az eredő tengelyirányú erő N, úgynevezett hosszirányú erő.
Eljárás használatával a szakaszok, azaz. E. figyelembe véve az egyensúlyt a bármely levágott része a rúd az intézkedés alapján külső terhelések és belső axiális erő N, azt kapjuk, hogy a hosszanti erő N egyenlő az algebrai összege a nyúlványok az összes külső erők, amelyek az egyik oldalon a keresztmetszet a tengelye a rúd.
A húzó-nyomó rúd keresztmetszete szokásos igénybevétel fordul elő, amelyek meghatározása a következő képlettel:
Erő feltétel:
Itt N - hosszirányú erő
F - keresztmetszeti terület,
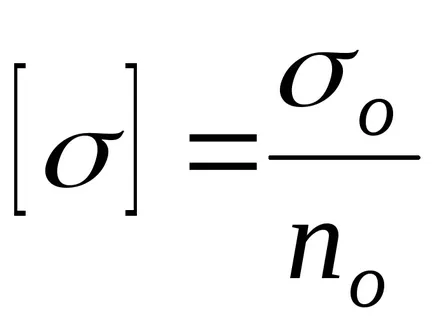
o - veszélyes feszültség anyagot (egyenlő a folyáshatár és a műanyag szilárdsága határa - a rideg)
NO - fő terhelési tényező.
Strength feltételt (2.2) ki tudja számítani a szükséges keresztmetszeti területe a rúd:
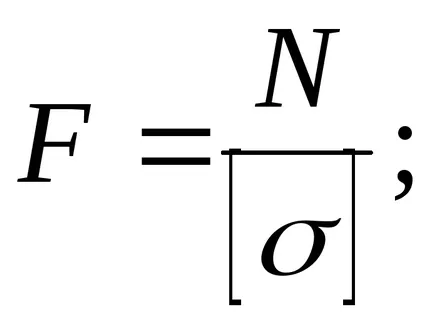
meghatározása vagy teherbíró képesség:
vagy ellenőrizze a megbízhatóságát a design.
Abszolút értéke a deformáció része a rúd állandó hosszirányú erő ezen a helyen ható, és az ismert keresztmetszeti területe által meghatározott Hooke-törvény:
ahol E - Young modulus vagy Young modulus.
A műveletet egy részét a hosszirányú rúd egyenletesen eloszlatott terhelése q intenzitását hosszirányú erő meghatározása a következő:
ahol No. - hosszirányú erő elején a cselekmény.
Ebben az esetben, a feszültség lehet képlettel számítottuk ki:
Deformáció csak az elosztott terhelés egyenlő:
Figyelembe véve az összes deformáció terhelési részt a rúd hossza L legegyszerűbb formula határozza meg:
ahol Nsr - középértéke hosszirányú erő egy részét a megoszló terhelés.
Ha a rendszer (kialakítás) a kötések (innen a reakciók kötvények) több, mint ahány egyenlet statikai, az ilyen rendszereket nevezzük statikailag határozatlan. Száma „extra” linkek fokának meghatározására redundancia a rendszer. Elkészítéséhez hiányzik egyenletek alapján az összeegyeztethetőség deformációk, figyelembe véve a geometriai szempontból a probléma, és megtalálja a kapcsolatát a deformáció szerkezeti elemek. Kifejező törzsből a Hooke-törvény erőfeszítései révén, a hiányzó egyenlet.
Példa №1. Ábrán látható. 2.1 lépcsős lényege a rendszer betöltése külső terhelések. Felépítéséhez szükséges ábrák a hosszanti irányú erők, a normál feszültséghez és elmozduláshoz.
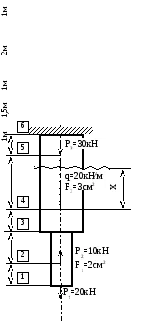
Mi határozza meg a területeket a rúd értékek a hosszirányú erők:
.
A diagram a hosszirányú erők ábrán látható. 2.2. Találunk minden helyszínen feszültség értékek:
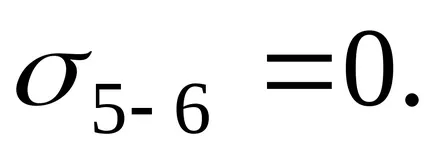
A diagram a normál feszültséget ábrán látható. 2.2.

elmozdulás diagram által épített rögzített vég, azaz, hogy a szorító, részben rögzítetten azaz 6 = 0. Továbbá, meghatározzuk mozgása az egyes pontok a rúd ....:
t. Hogy. N5-6 = 0, megkapjuk
,
Az állomáson 4-5 van egy szélsőérték diagramja elmozdulások szekcionált Ho. ahol a hosszirányú erő nulla. Keressük az értéke Ho feltételek:
N (O) = - 30 + 0 = qho,
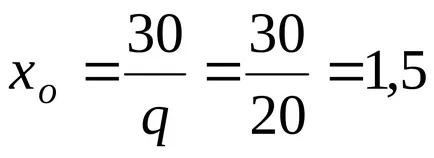
majd tolja a szélsőséges érték ebben a régióban is:
Határozza meg a mozgó részt a „3”, ami egyenlő a deformáció része 6-3, bizonyos alakváltozások részletekben 5-6 és 4-5:
elmozdulás diagramot ábrán látható. 2.2.
Elemzés a diagramok azt mutatják, hogy koncentrált erők hatására ugrik a diagramok «N» és «», és a diagram «» - törje. Azokon a területeken, egy elosztott terhelés diagramja «N» és «» változó, egy diagram «» változik parabolikus. Egy éles változás keresztmetszetű okoz ugrás a rajz «» (a „3”).
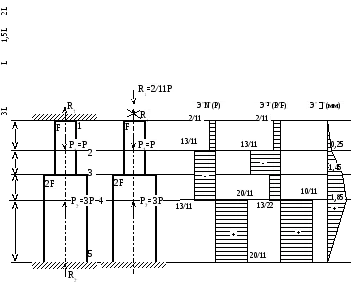
Példa №2. Lépcsős nyaláb befogva mindkét végén, és betöltve egy rendszer külső terhelések, ábrán látható. 2.3. Anyag fűrészáru St.3 acél folyáshatára = 240 MPa t és az alapvető biztonsági tényező Fr = 1,5.
A rugalmassági modulus E = 2 × 10 5 MPa. keresztmetszeti területe, hogy F = 4 cm 2.
Construct Epure «N» a «F» frakciók;
Construct Epure «» a «F / F» frakciók;
Határozza feltételei szilárdsági terhelhetősége [F];
Egy adott terhelési [P] konstrukció Epure elmozdulások «».
Az egyensúlyi reakció egyenletek határozzák meg a támaszok (ábra. 2.4a).
Van egy rendszer konvergens erők, melyek a mérleg egyenlet:
E. Statika egy egyenlet két ismeretlen R1 és R2. A rendszer egyszerre statikailag határozatlan.
Tekintsük a geometriai szempontból a probléma. Mivel a referencia szakasz rögzítve van, ezek viszonylagos mozgását nullával egyenlő, azaz. E.
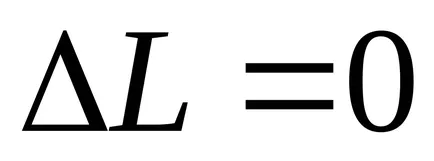
Felszabadítani egyik végét a rúd (felső) ábrán látható módon. 2.4b. Összhangban a szuperpozíció elve alapján, a relatív elmozdulást úgy definiáljuk, mint az összeg a deformáció a ható terhelés a rúd:
;
Írunk az utolsó kifejezés helyett egyes összetevők felhasználásával Hooke-törvény:
.
Megszorozzuk mindkét oldalán az egyenlet által
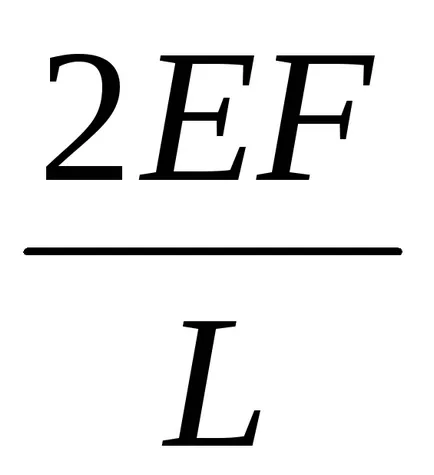
,
A „mínusz” jel azt jelzi, hogy R1 az ellenkező irányba. Ábra. 2.4 régi R1 irányban áthúzott, de tényleg egy lefelé irányuló reakciót
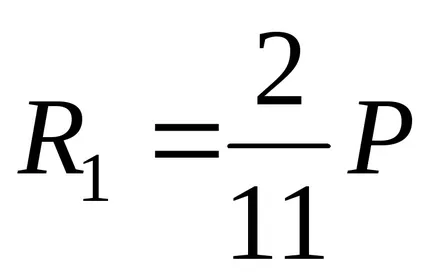
Construct Epure «N» frakciókban „P” (ábra 2.4c.), Amelyhez levelet a kifejezéseket hosszirányú erőt minden egyes részét a rúd:
Tekintettel a keresztmetszeti területek mindegyik rész megtalálni és megépíteni a feszültség diagramjai normális feszültség, mint egy frakciót P / F (ábra 2,4 g.):
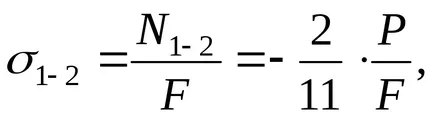
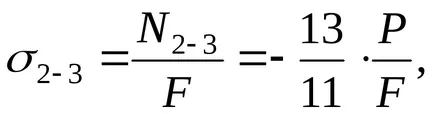
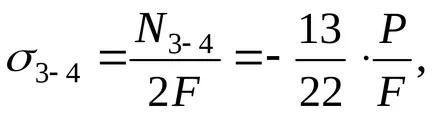
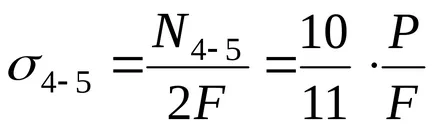
Nyilvánvaló, hogy a legnagyobb stressz
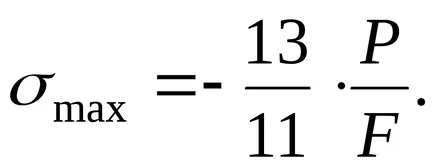
Írunk a feltétellel erőssége:
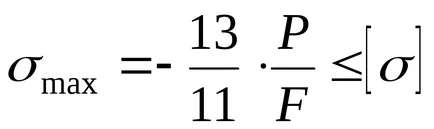
Construct Epure elmozdulások meghatározása ellensúlyozza a jellegzetes pontok a rúd.
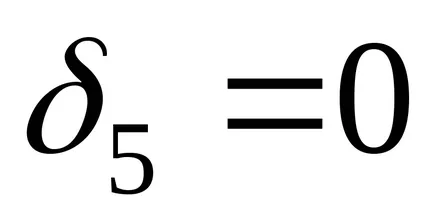
Amint látható a számítási eredményeket, mozgó hogy a megszorított szakaszok 1 és 5 nulla, amely megerősíti a helyességét a megoldás. elmozdulás ábrán látható diagram. 2.4D.
Példa №3. Teljesen merev gerenda OB kapcsolódik csuklósan a O. mentési AC tapadást és HP. Betöltött gerenda P erő = 100 kN. Anyag és hát tolóerő - acél cm. 4 egy folyáshatár = 300 MPa t. Határozzuk meg a keresztmetszeti területe a biztonsági és a vontatási - F1 és F2. Ha F1 / F2 = ½. A számítások figyelembe a biztonsági tényező NT = 1,5.
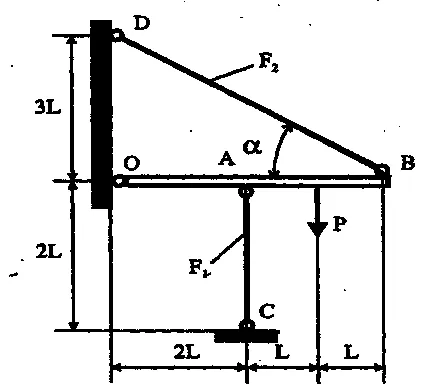
Készíts egy tervet becsült erőkifejtés (ábra. 2.6).
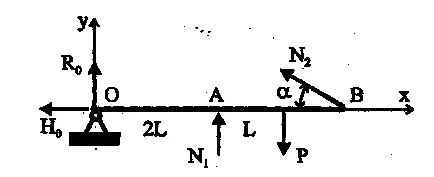
Az egyenlet egyensúlyi:
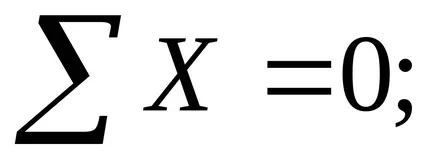
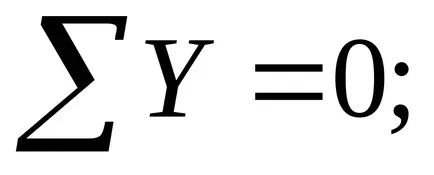
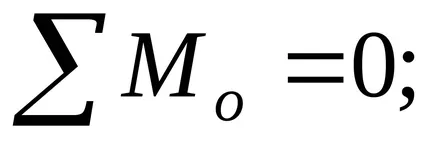
Ennek eredményeként megkapjuk három egyenletet négy ismeretlen statikus Ro. De. N1 és N2. E. Ha a rendszer statikailag határozatlan.
A nyilvánosságra hozatala redundancia konstrukció terv mozgását foglalja magában (ábra. 2.7).

Az intézkedés alapján az F erő BAW merev fűrészárut körül forog az O pont a pont, A és B, illetve elfoglalhatja az A1 és a B1. A hasonlóság háromszögek OVV1 OAA1, valamint:
A szög háromszög VV1V
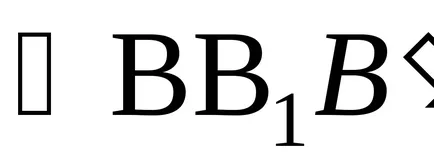
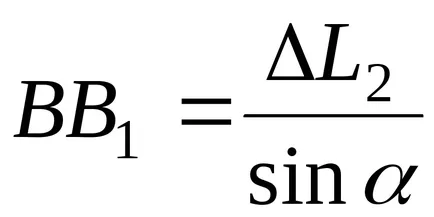
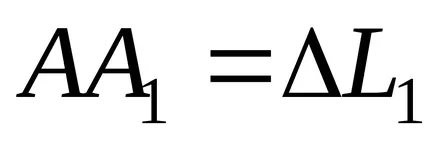
.
expressz
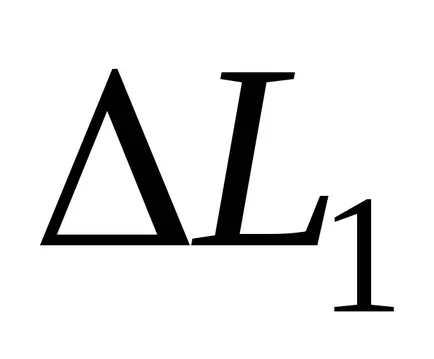
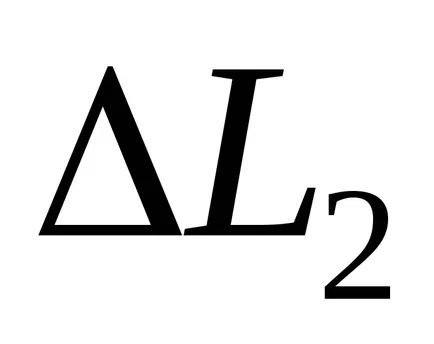
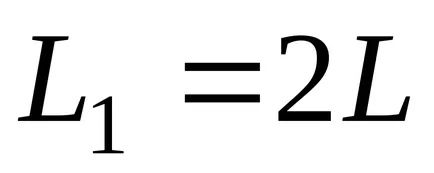
feltéve, hogy
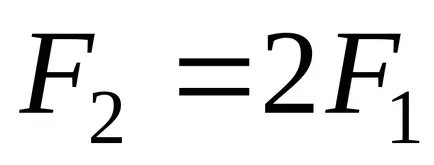
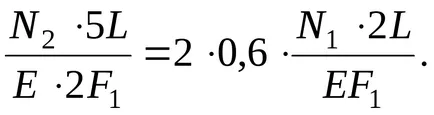
Miután egyszerűsítve ez a kifejezés megkapjuk a hiányzó egyenlet a következő formában:
Problémák az egyenletből, valamint a harmadik egyenlet az egyensúly és figyelembe véve, hogy
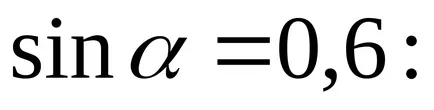
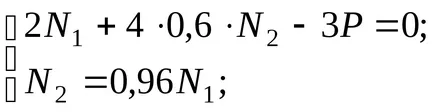
Kapunk az értéke erőfeszítés:
Határozza meg a terület a keresztmetszete a rudak. Ehhez először megtalálni a megengedett feszültség:
Írja erőt feltétele tartalék AC és meghatározzák a keresztmetszeti terület:
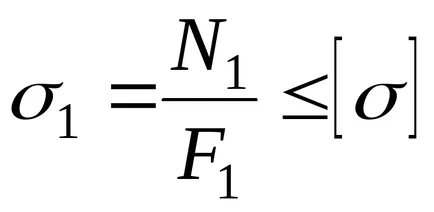
.
Alatti terület arányából lelet:
Ezután a feltétele a tartósság az AC vontató igazolta a korrekt terület meghatározására
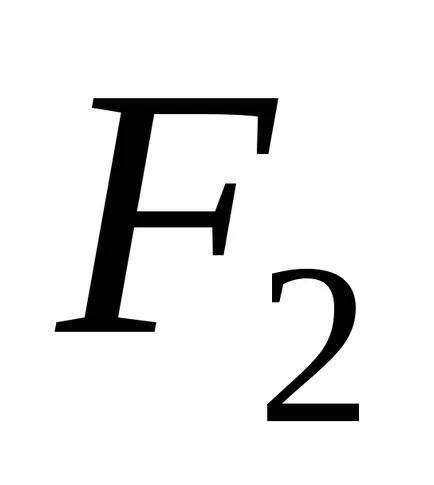
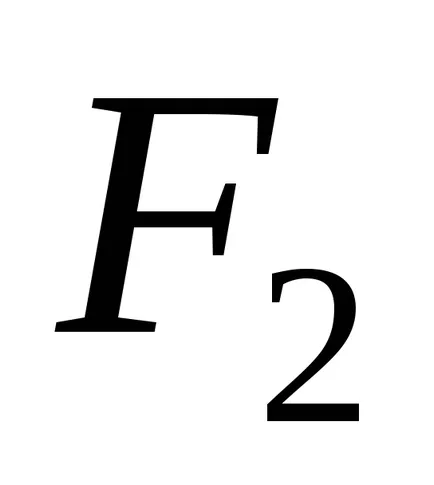

Ellenőrizze az erejét a rúd VD:
.
Emiatt a szerkezeti szilárdságot biztosított.