Rational gyökerei egy egész együtthatós polinom
A kérdés, hogy találjanak f (x) polinom racionális gyökerek
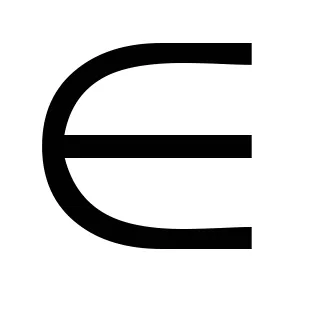
Szükséges, de nem elégséges feltételei a létezését racionális gyökerei egy egész együtthatós polinom által adott alábbi tétel.
Tétel 6.1 (a racionális gyökereit egy egész együtthatós polinom) .Ha
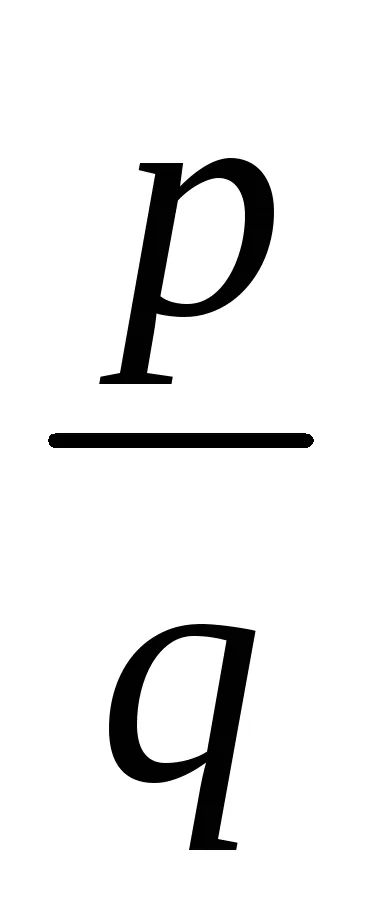
tétel 6.2.Esli
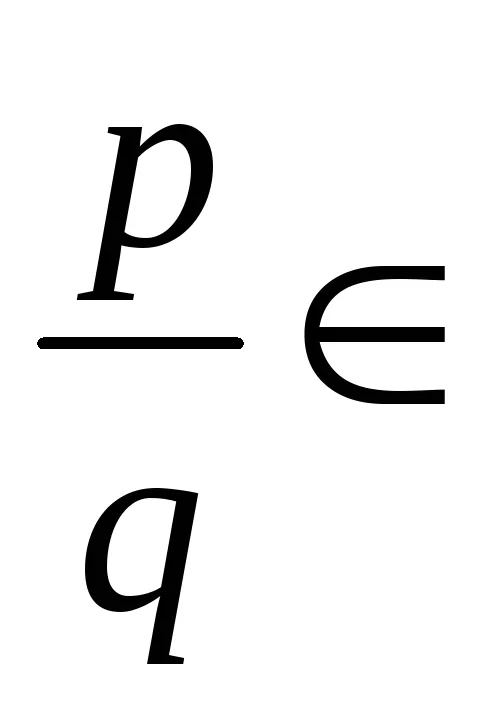
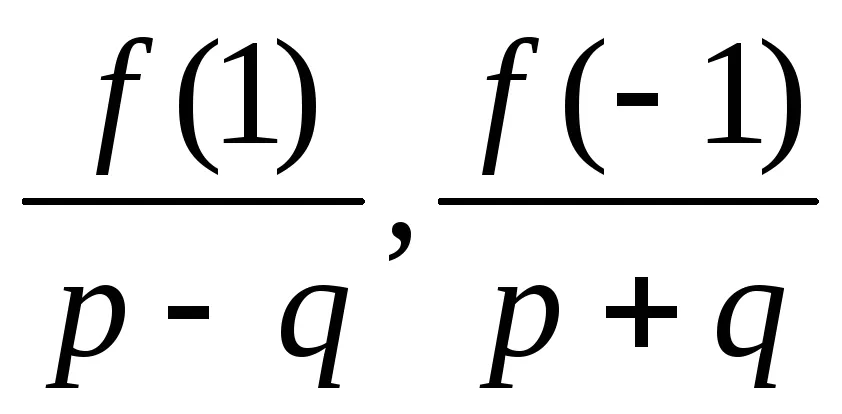
Példa. Találd meg az összes racionális gyökerei a polinom
1. Tétel 6.1: ha
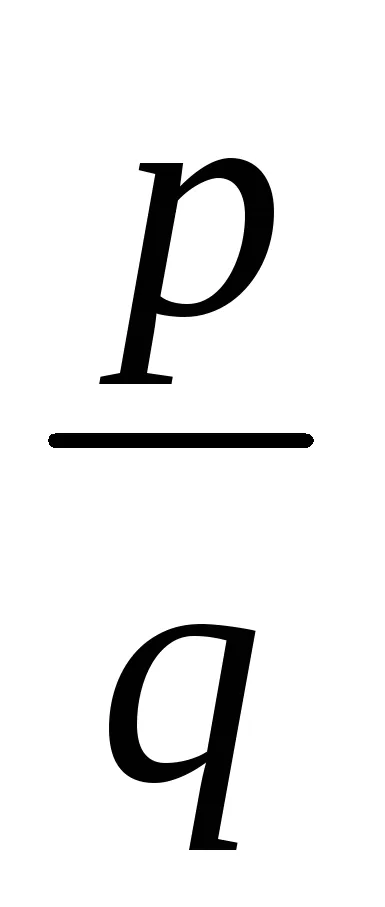


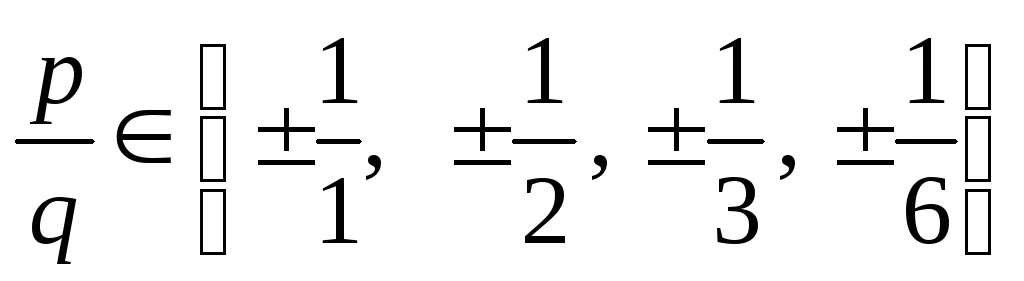
2. Ismeretes, hogy a (következmény 5.3), a szám egy egy gyökér a polinom f (x) akkor és csak akkor, ha f (x) van osztva (x - a).
Ezért, annak ellenőrzésére, hogy az 1 és -1 gyökerei a polinom f (x) használhatja a Horner rendszer:
Kapott: Q (
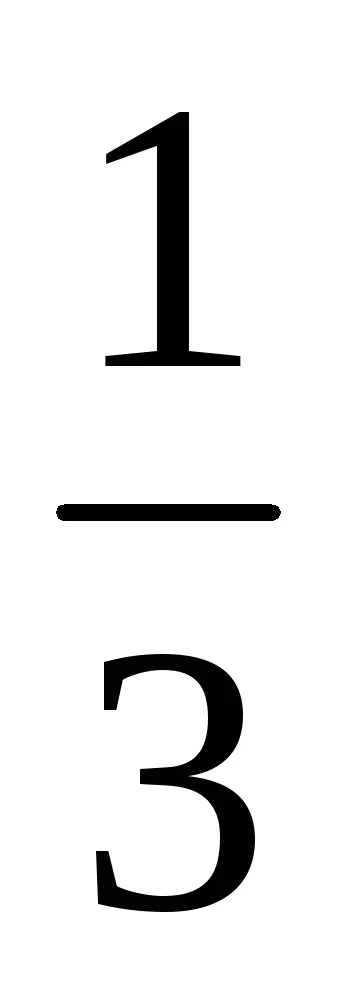
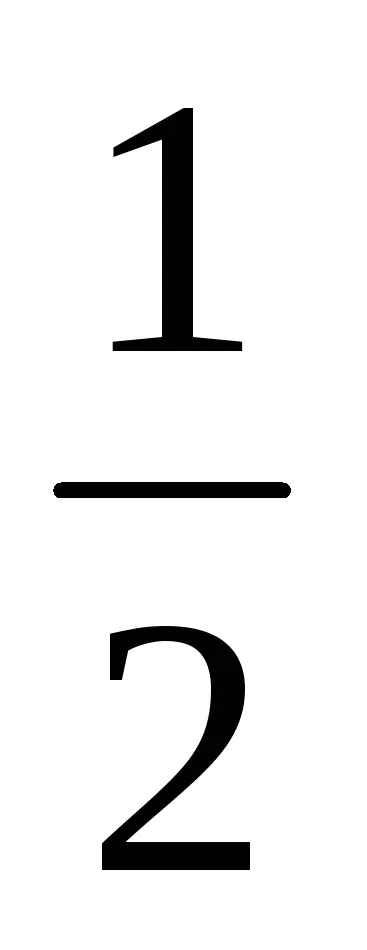
Mentesség algebrai irracionalitásnak nevezőjében a frakció
Az iskola természetesen megoldására bizonyos típusú problémák megjelenése az irracionalitás a nevezőben a frakció elegendő szaporodnak a számláló és a nevező száma konjugált nevező.
Itt, a nevezőben a általános képletű aktivált Rövidítés szorzás (a különbség a négyzetek), amely lehetővé teszi a szabad irracionalitásának a nevezőben.
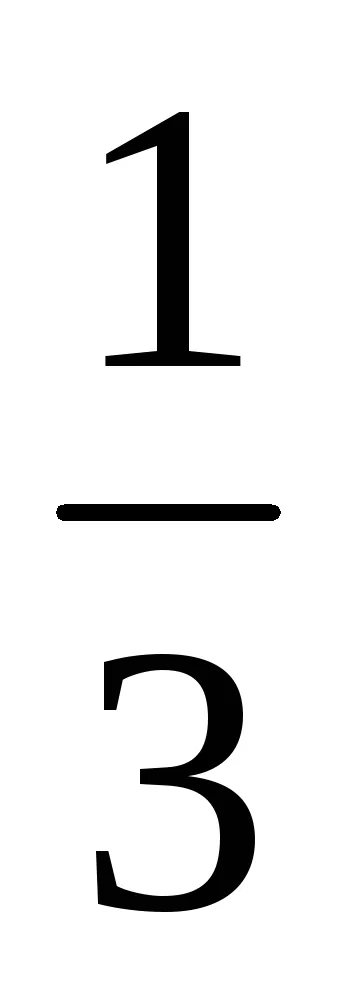
2. Megszabadulni az irracionalitás, a tört nevezőjében a
t =
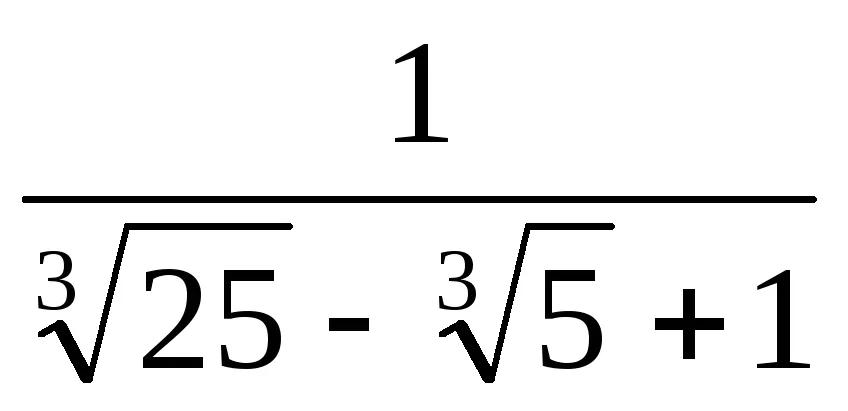
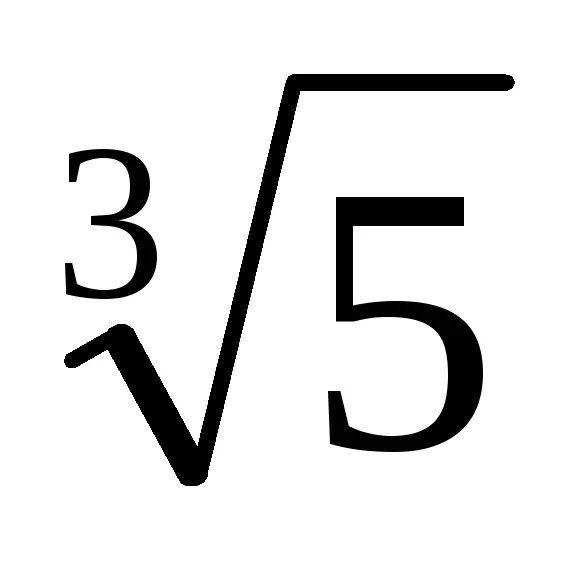
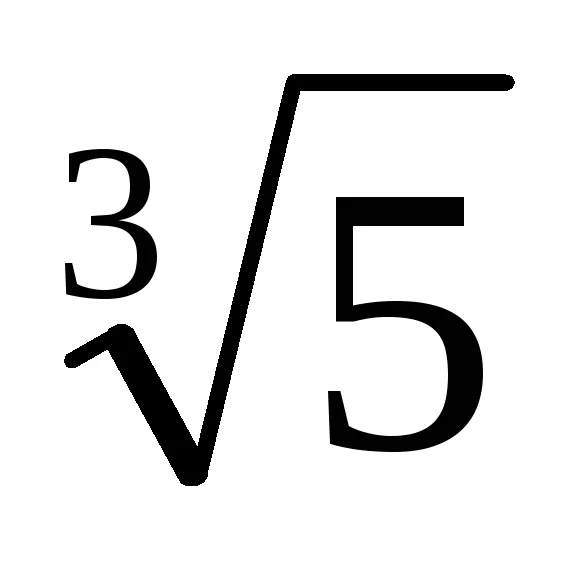
Azokban az esetekben, ahol a képletek rövidített szorzást nem működik, akkor más módszerekkel. Az alábbiakban megfogalmazzuk a tétel bizonyítása, amelyek különösen lehetővé teszik az algoritmus, hogy megtalálja mentességet a irracionalitás a nevezőben a frakció a bonyolultabb helyzetekben is.
Definíció 6.1. A száma Z hívják algebrai felett polemF. ha létezik olyan polinom f (x)
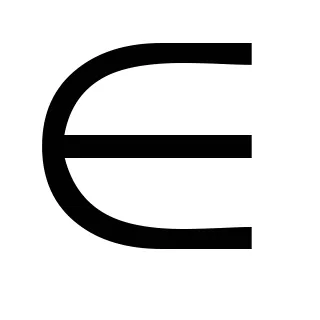
Meghatározása 6.2.Stepenyu algebrai fölött polemFchislaz nevezett fokú irreducibilis polinom a mező fölé F p (x)
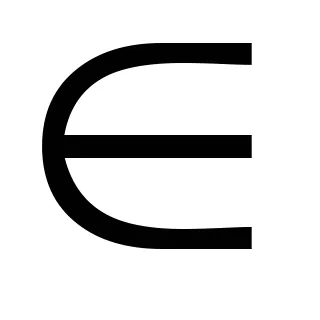
Példa. Megmutatjuk, hogy a száma Z =
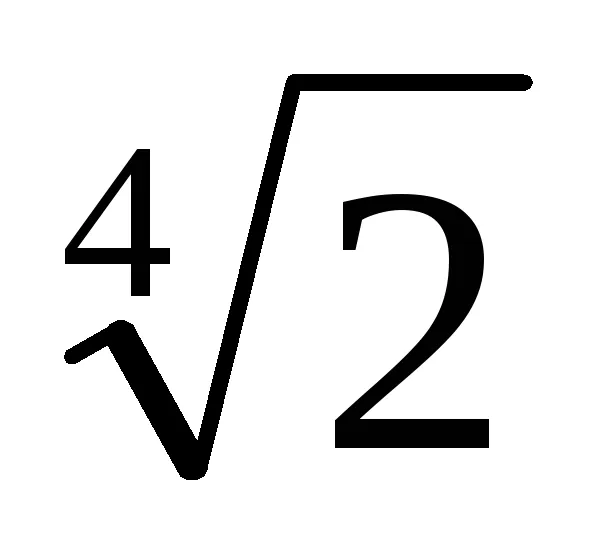
Azt találjuk, redukálhatatlan polinom a mező fölé Q p (x), a gyökér, amely X =
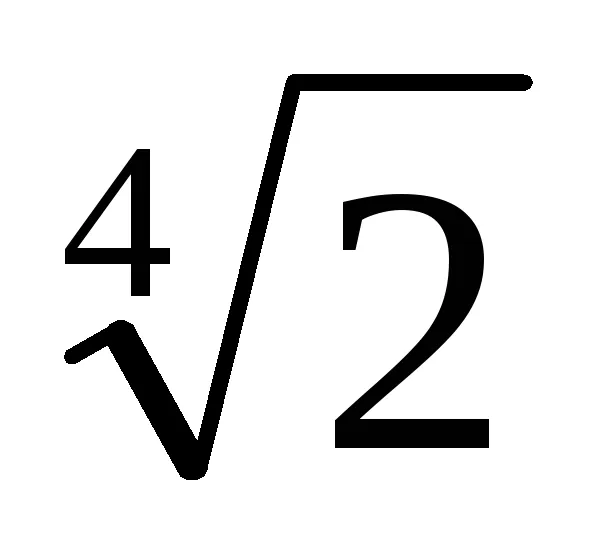
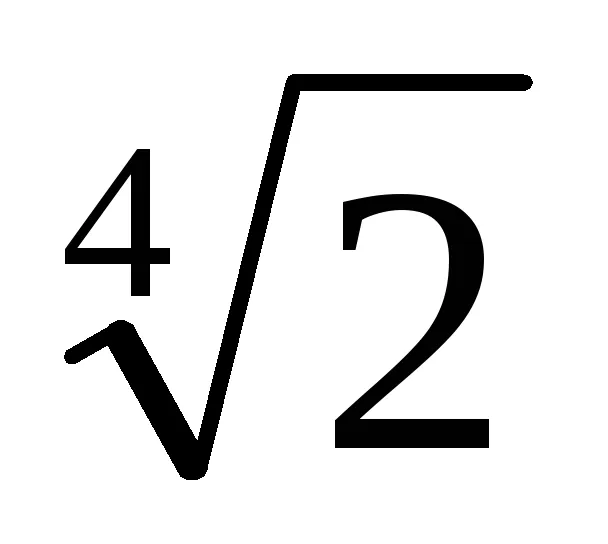
6.3 Tétel (a kibocsátás algebrai irracionalitás a nevező) .Pustz- algebrai fölött polemFstepenin. Expression vidat =
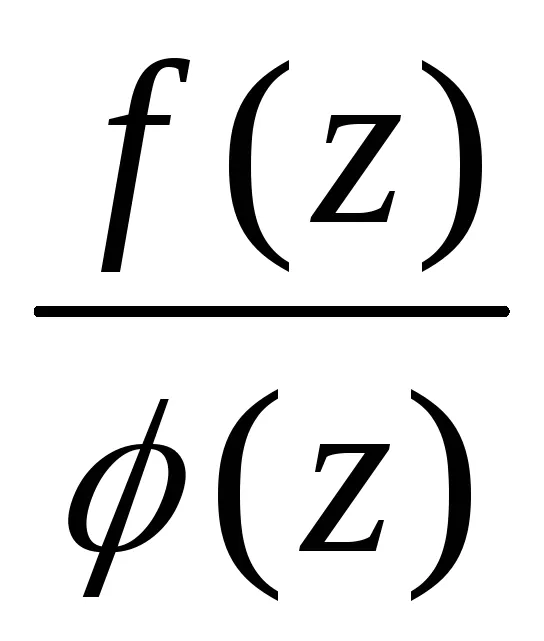


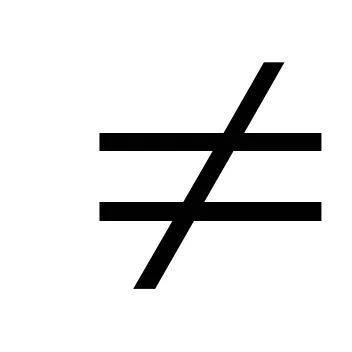
Ez lehet egyedileg képviselt formájában:
t = cn-1zn-1 + cn-2Zn-2 + ... + C1Z + c0. ci
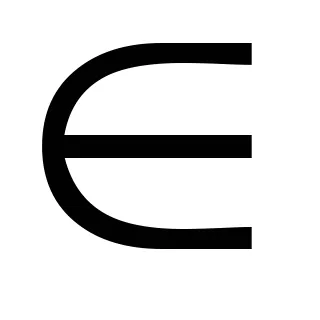
Felszabadító irracionalitás algoritmus bemutatja egy konkrét példát a nevezőben.
Példa. Szabad a irracionalitás a nevezőben:
1. A nevező a frakció a polinom értékét

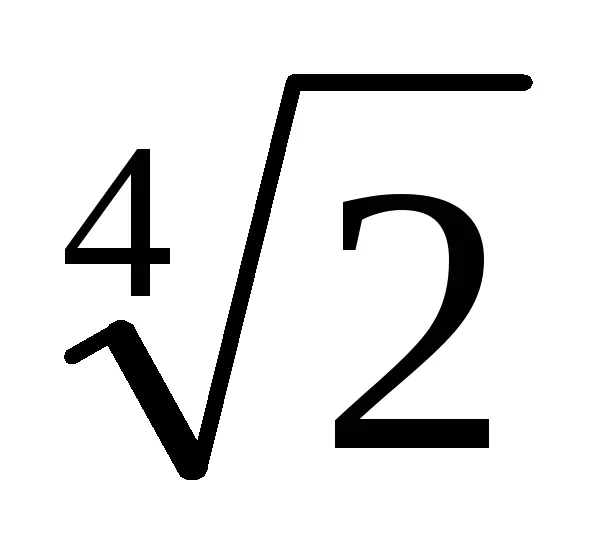
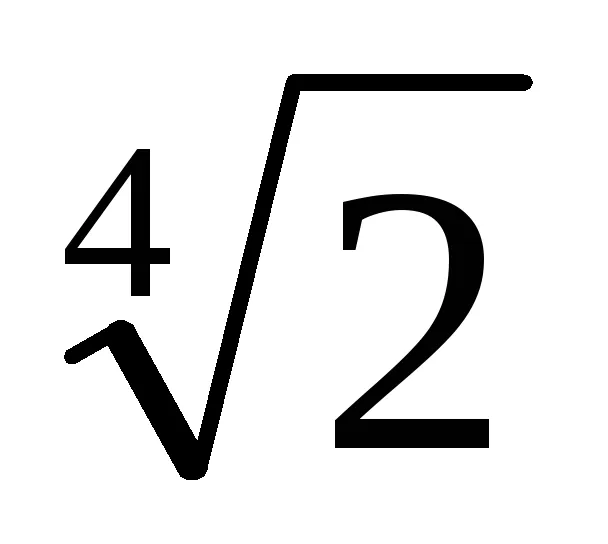
2. Keresse meg a lineáris kiterjesztése a GCD (

-x-2 -
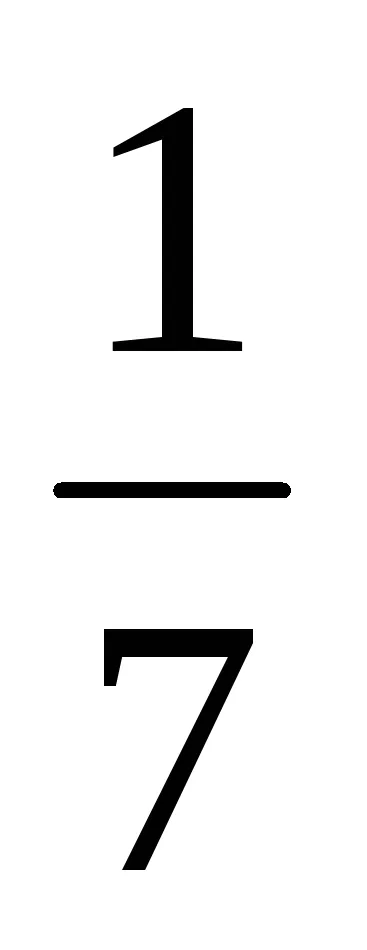
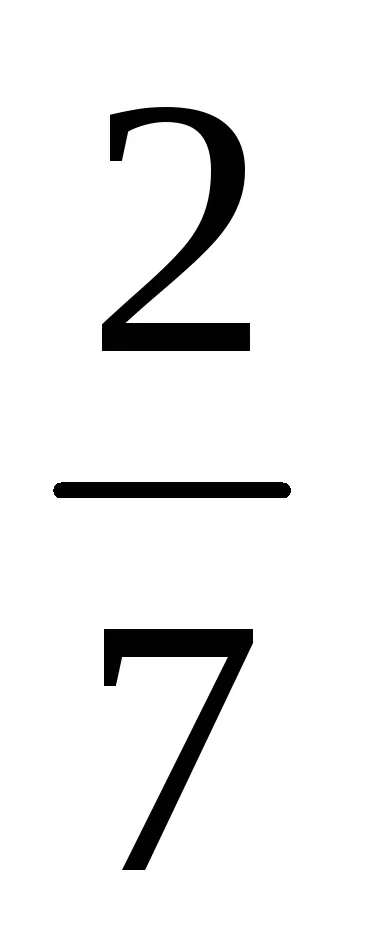
Tehát GCD (

Írunk szekvencia Euclid, a jelölést polinomok.
p (x) =




Behelyettesítve egyenlet 7 = r2 (X) =




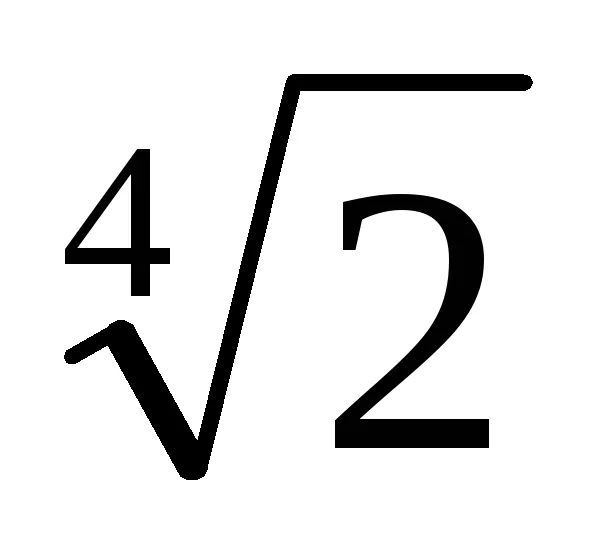
(1 -
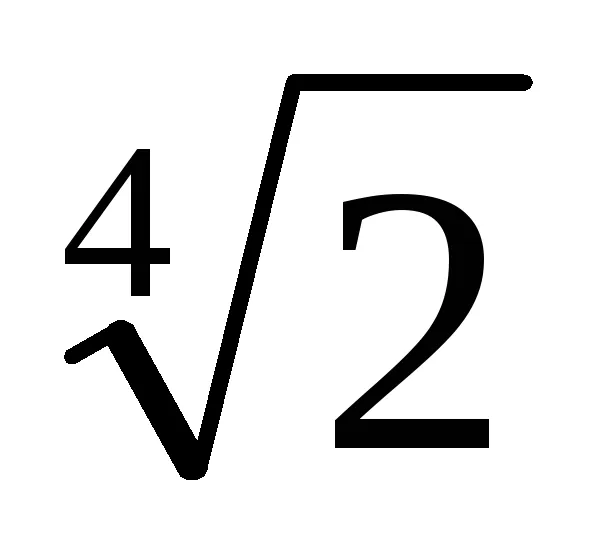
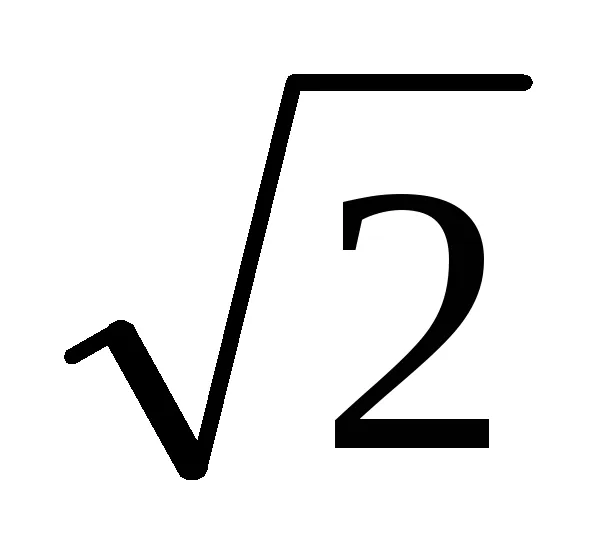
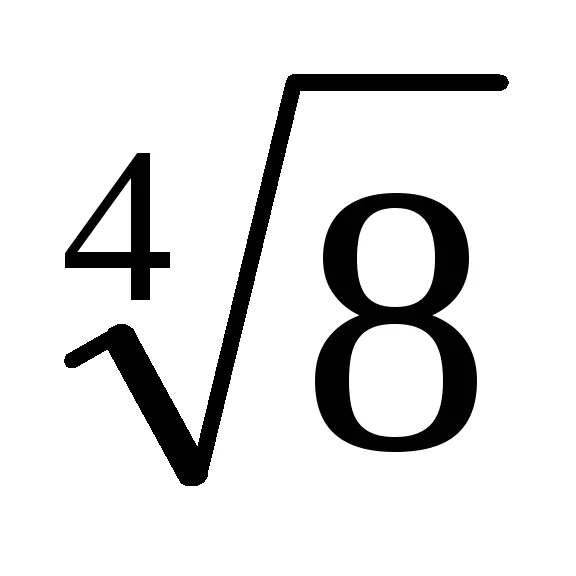
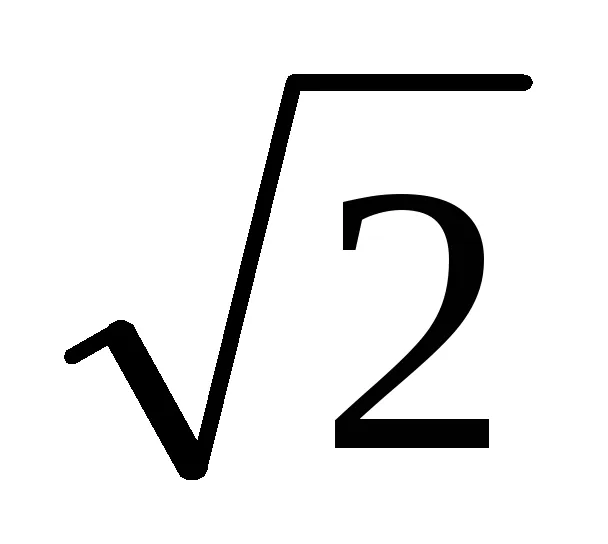
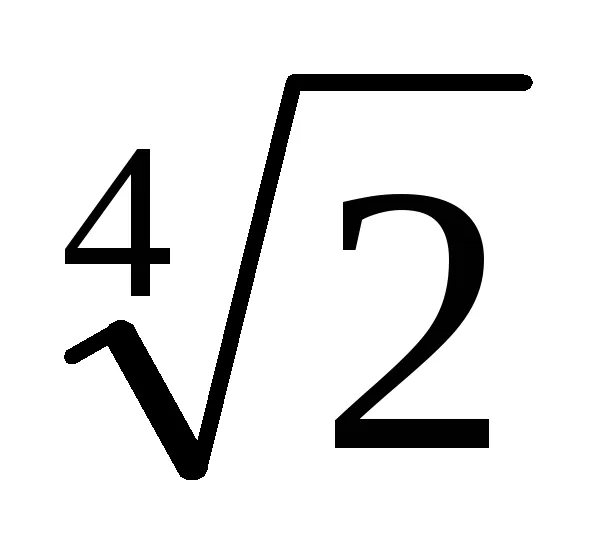
3. (1) egyenlet azt jelenti, hogy ha a nevező szorozva száma t m = [1 + (-
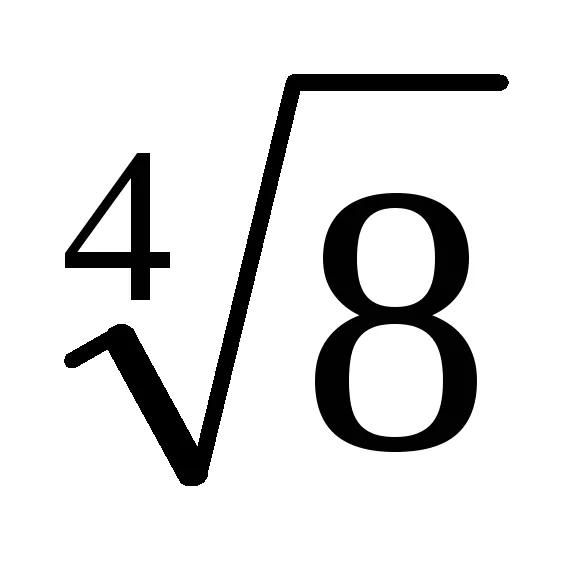
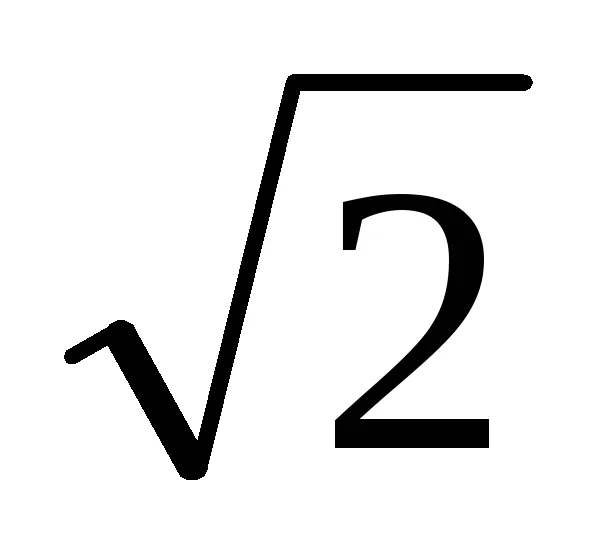
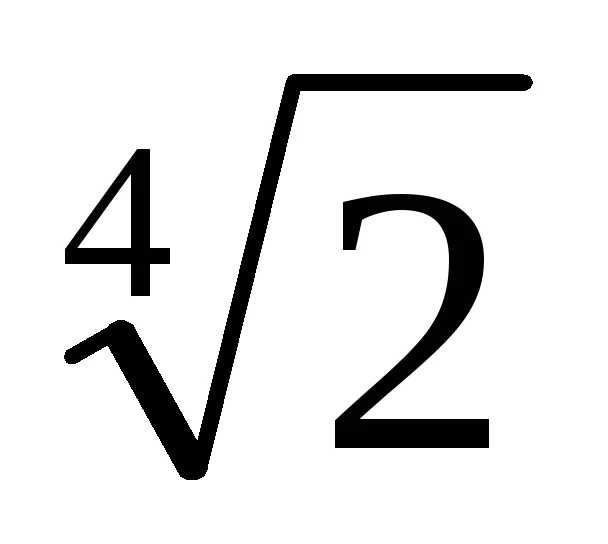
MÓDSZERTAN 16. lecke Tárgy: Normál nézet polinom
Típusa tanulság: a leckét ellenőrzéséhez ismeretek és készségek
- ellenőrizze polinom készségek vezet formanyomtatvány
- hogy fejlessze a hallgatók logikus gondolkodás, a figyelem
1. Végezze el a mondat:
a) kifejezés, amely tartalmaz egy összeget egytagú említett ... (polinom).
b) polinom álló szabványos egytagú, és nem tartalmaz ilyen feltételek az úgynevezett ... (normál polinom).
c) A legnagyobb fokú az egytagú belépő egy polinom hívják formanyomtatvány ... (a polinom foka).
g) meghatározása előtt szükségessége mértékének ... (hogy azt a szabványos formában).
d) meghatározza a polinom értékét kell tennie az első ... (képzelni egy polinom formanyomtatvány), második ... (a változó értékét a kifejezés).
2. Keresse meg az értékét a polinom:
3. Hozd polinom a szokásos formában
4. Hozd polinom a formanyomtatvány, és megtudja, milyen az x értéke 1: