Skaláris termék és tulajdonságai
Zéró skalár termék két a és b vektorok egy szám egyenlő a termék hosszának ezen vektorok a koszinusz a szög Internat.
Jelöljük ab, a * b (vagy (A, B)). Ily módon, definíció szerint,
A tulajdonságok a skalár termék:
1. A skalár termék a kommutativitás: ab = ba

5. Ha a a és b vektorok (nem nulla) kölcsönösen merőleges, majd a belső termék nulla, m. E. Ha a ^ b, AB = 0, akkor. Az ellenkezője is tart: ha ab = 0, és 0 A'¹b, majd a ^ b
.
Feltételek merőleges vektor
Két nem nulla vektort nevezzük merőleges. ha a köztük lévő szög egyenlő kilencven fokkal (radiánban).
Tétel: A szögletességét két nem nulla vektorok és a szükséges és elégséges az, hogy skalár szorzat értéke nulla, azaz, hogy az egyenlőséget.
A szög a vektorok
A szög a két vektor közötti. késleltetve egyetlen ponton, az úgynevezett legrövidebb szög, amellyel, hogy megforduljon egyik vektor annak eredetét a helyzetét CO-irányított egy másik vektorral.
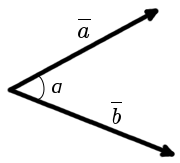
A képlet kiszámításához közötti szög a vektorok: