söprés módszer
Továbbá, segítségével egyenletek (1.7) és a progonochnyh együtthatók a kifejezések (1.8) és (1.9) vannak egymás után kiszámítja a xn-1. xn-2. x1.
Végrehajtása során a sweep módszer kell vizsgálni, hogy figyelemmel
vagy legalább egy bi van a szigorú egyenlőtlenség (1.12), a különbséget a „0” -t kell hagyni, és a rendszer egy egyedülálló megoldás.
Megjegyezzük, hogy a feltétel (1,12) is elegendő, de nem szükséges. Bizonyos esetekben, jól kondicionált rendszerek (1.7) a sweep módszer lehet stabil és nem-megfelelést feltétel (1,12).
Reakcióvázlat sweep-módszer algoritmus formája lehet az 1.2 ábrán látható.
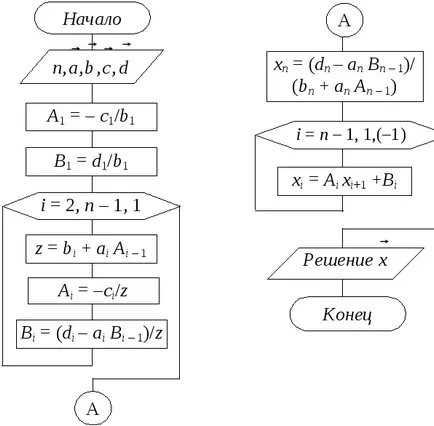
1.2 ábra - blokkvázlata a sweep módszer
Iteratív megoldási módjait, Slough
Az előnye, hogy iteratív módszerek azok alkalmazhatóságát a rosszul kondicionált rendszerek és magasabb rendű, samoispravlyaemost és könnyen megvalósítható a számítógépen. Iteratív kiszámításának az elején a munkát igényel kezdeti közelítését a kívánt megoldás.
Meg kell jegyezni, hogy a feltételek és a konvergencia sebessége az iteratív folyamat nagyban függ a rendszer tulajdonságai A mátrix és a választott kezdeti közelítések.
Módszer alkalmazásának ismétlések eredeti rendszert meg kell hozni az iteratív elme
majd hajtsa végre az iteratív folyamat a kiújulás képletek:
A mátrix G és a vektor
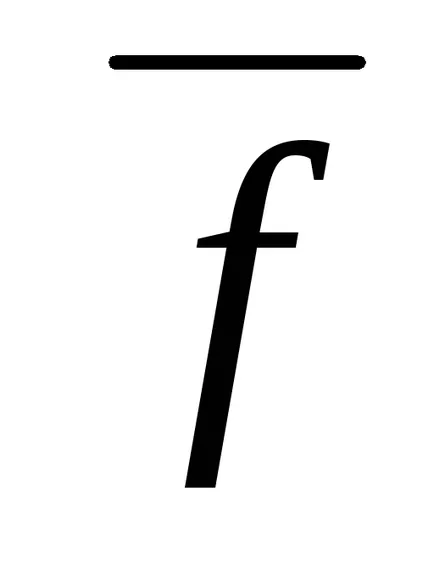
A módszer konvergenciáját (1,13 *) szükséges és elégséges, hogy | i (G) | <1, где i (G ) — все собственные значения матрицы G. Сходимость будет и в случае, если ||G || <1, ибо |i (G )| < ||G || ( — любой).
A szimbólum ||. || Ez a norma a mátrix. Annak megállapítására értéke gyakran megáll, hogy ellenőrizze két feltétele van:
|| G || =
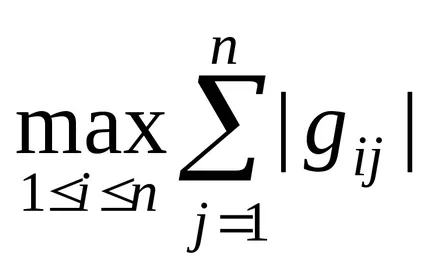
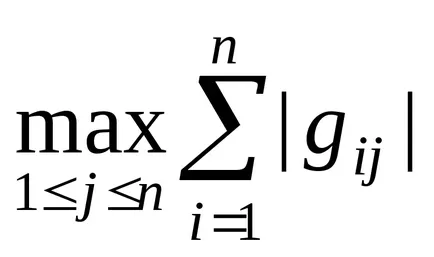
ahol
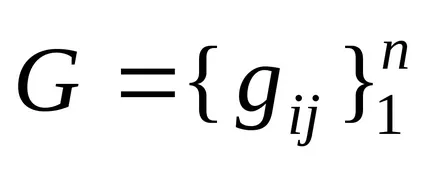
Amikor a körülmények (1.14) vagy (1.15) teljesül, az iterációs módszer konvergál bármely kezdeti közelítését
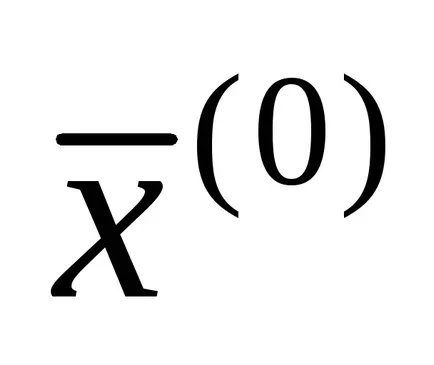
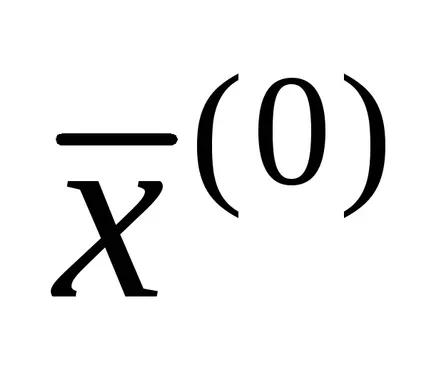
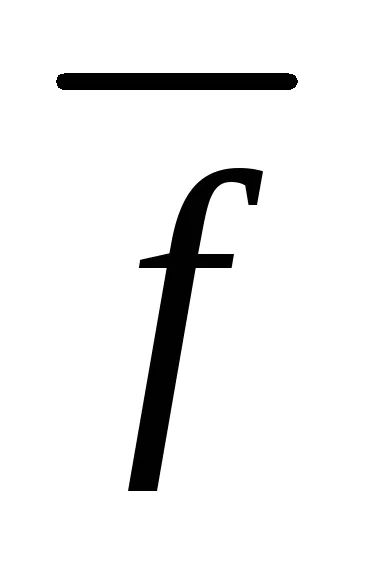
Ha az állapot (1,15), majd az átalakítás, hogy az iteratív formájában (1,13) lefolytathatjuk egyszerűen megoldásával egyes i-edik egyenlete rendszer (1) képest xi a következő kiújulás képletek:
Ha az A mátrix nem diagonális dominancia, el kell érni, annak bármely lineáris transzformációk, amelyek nem sértik azok egyenértékűségét.