Számított szimulációs modell egységek cistem automatikus szabályozása Mathcad - 2. rész
Logaritmikus frekvencia karakterisztika
A legtöbb esetben, az amplitúdó és fázis frekvencia karakterisztika ábrázolt logaritmikus skálán. Ilyen logaritmikus frekvencia jellemzői nagyon kényelmes mérnöki számítások.
Az építőiparban a logaritmikus amplitúdójú frekvencia jelleggörbét (LACHH) függőleges tengelyén értékét képviseli
A mértékegység, amelyre a decibel (dB). Az abszcisszán tengely W jelentése a logaritmikus skálán (8. ábra).
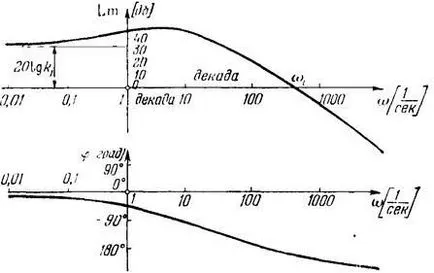
8. ábra. Logaritmikus frekvencia jellemzőit.
Egységes egység az x-tengely egy évtizede - minden szegmens, amelyben a frekvencia értékét növeli tízszeresére. A metszéspontja az abszcisszával LACHH nevezett WSR levágási frekvencia.
Az építőiparban a logaritmikus fázis a frekvencia karakterisztika (LPC) szögek számít Y jelentése a függőleges tengely a normál méretű szögfokokban. A abszcisszán ábrázoljuk mentén a frekvencia W marad a logaritmikus skálán.
Fontos figyelembe venni, hogy az abszcisszán (L = 0) értékének felel meg k = 1. t. e. áthaladás egy link jelamplitúdó megváltoztatása nélkül az amplitúdó. LACHH felső fél sík az értékek k> 1 (amplitúdó erősítés), és az alsó fél-sík - értékeit<1 (ослабление амплитуды).
2. A főbb egységek.
Típusú egységek automatikus ellenőrző és szabályozó rendszerek függően különböznek, hogy milyen típusú átviteli függvények (vagy differenciálegyenletek), amelyek meghatározzák a dinamikus tulajdonságok és jellemzőit.
Tipikus egységek jellemzi dinamikus differenciálegyenletek érdekében nem nagyobb, mint kettő.
Attól függően, hogy milyen típusú differenciálegyenletek az automatikus vezérlő elmélet különbséget tesz a következő alapvető típusú kapcsolatok:
-inertialess (arányos vagy erősítő);
-elsőrendű tehetetlenségi (vagy aperiodikus);
-a tehetetlensége a második sorrendben;
A főbb típusai a linkeket a három csoportba oszthatók:
Pozicionális egységek azok, amelyekben az átviteli függvény
Polinomok Bm (p) és egy (p) állandó tekintetben megegyeznek az 1, azaz, ezek a linkek a statikus jellemző Yust = k × Khust (P = 0W (p) = k =), meghatározza azok egyensúlyi állapot - .. Pozicionális tulajdonság .
A differenciáló elem az átviteli függvény kifejezés nem konstans a számláló, azaz egyszer differenciáló elem B0 = 0 ..:
Ahol Bm-1 (p) van a konstans értéke 1, és K = - erősítés.
Az átviteli függvények az integráló komponens rendre:
Amennyiben egy-1 (p) van egy szabad kifejezés egyenlő 1.
A tudás a jellegzetes egységek kifizetéséhez szükséges rendszerek.
2.1. Ideális erősítő (inertialess) link.
Egyenlet és az átviteli függvényt szint:
Példák szabadonfutó hajtómű, egy feszültségosztó, a szög érzékelőket, a pillanatnyi teljesítmény és mtsai. (Ábra9).
Ábra. 9. PÉLDA szabadonfutó egységek.
Tény, hogy nincs szabadonfutó egységet. Általában tekinthető ideális CAP-egységek tehetetlensége sokkal kisebb, mint a tehetetlenség az egyéb kapcsolatok. A legtöbb esetben a különböző érzékelők és előerősítők. Inerciális késedelem sok mérési elemeinek automatikus rendszerek (ferde szögben érzékelők, fénysorompók, magneto-érzékelők) kicsi, így ők tekinthetők inertialess linkeket.
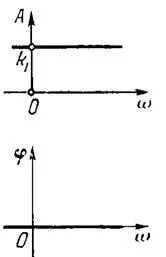
10. ábra. Frekvencia karakterisztika szabadonfutó egységet
2.2. Inerciális (aperiodikus) link.
Egyenlet és az átviteli függvényt szint:
Ahol T - időállandó; K - Link átviteli sebesség.
Példák a tehetetlenségi (aperiodikus) egységek egyenáramú motorok, amikor X (t) - tápfeszültség, és Y (t) - a szögsebesség a tengely W (t); két-fázisú aszinkron motorok; Erősítők inerciális lag figyelembe; masszív test, ha a bemeneti változót számolja meg a bejövő hő időegységenként, és a Q kimenet - a hőmérséklet bármely pontján a test belsejében, stb). L-R-lánc (11. ábra).
11. ábra. Példa tehetetlenségi linkre.
12. ábra. APFC tehetetlenségi elem.
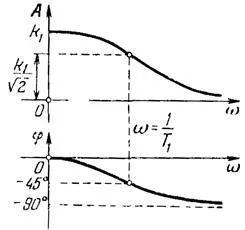
13. ábra. Az amplitúdó-frekvencia és fázis válasz a tehetetlenségi egység
A logaritmikus amplitúdó-frekvencia karakterisztika a formája:
Ez jellemző az a asymptote:
Utolsó asymptote hajlik egyenes meredekséggel -20 dB / dekád, és az első - a vízszintes vonal. Aszimptotákkal pontban metszik egymást WC =. LACHH maga közel ezeket aszimptotákkal.
Logaritmikus rácsot a frekvencia tengelyen a sarokban gyakorisága Wc = (lásd 14. ábra). A frekvenciák kevesebb, mint a párzási, t. E. Amikor W<. можно пренебречь вторым слагаемым под корнем, тогда левее сопрягающей частоты можно заменить L(W) приближенным выражением
Ez a kifejezés megfelel a vízszintes vonal. A nagyobb frekvenciájú párosodási W> a kifejezés L (W) elhanyagolhatóak 1 alatt a gyökér. Akkor L (W) = 20lgk-20lg (WT). A második kifejezés egy egyenes vonal ferdén -20 dB / évtizedben. A szaggatott vonal az úgynevezett aszimptotikus LACHH. A legnagyobb eltérés a pontos LACHH aszimptotikus körülbelül 3 dB-es frekvencián konjugáció, azaz a. Hogy.:
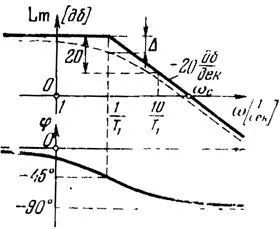
14. ábra. LACHH tehetetlenségi elem.
Az átmenet függvény szerint a döntési egység egyenlet X (t) = 1 (t) és a nulla kezdeti feltételek (ábra15):
15. ábra. Az átmenet funkciója a tehetetlenségi egység.
Az időállandó határozza meg a lejtőn a T érintő elején a görbe (15. ábra). Következésképpen, a T értéke jellemzi a perzisztencia szinten, azaz. E. Az időtartam a tranziens. Elméletileg ez átmeneti folyamat tart a végtelenségig. Gyakorlatilag ezt a linket egy ideig átmeneti megérteni azt az időtartamot, amely után a Ts egyenlőtlenséget:
Amikor alkalmazni a bemeneti jel X0 Közbensőkör után tranziens koordináta Y (t) mereven össze van kötve, hogy a bemenet:
2.3. Oszcilláló egység.
Egyenlet és az átviteli függvényt szint:
Az általánosan elfogadott rekord az átviteli függvény a vibrációs szintet formájában:
Amplitúdó és fázis frekvenciaválasz (16. ábra) Link:
16. ábra. A frekvencia jellemzőit a oszcillációs tag.
A logaritmikus amplitúdójú frekvenciamenet egység
At értékek 0,5 17. ábra. Logaritmikus frekvencia karakterisztikája oszcilláló tag. Ha X<0,5. то получается заметный максимум (рис.17). Максимум характеризуется превышением Hm Az egyszerűsített számítást, hogy megtalálják Hm elég közelítés (lásd 17. ábra) .: Az átmenet funkciója a rezgési szintet a 18. ábrán látható. 18. ábra. Az átmenet funkciója a vibrációs szintet. Ha X = 1 egy aperiodikus oszcillációk degenerált folyamatot. Ha X = 0 rezgéseket csillapítatlan (időszakos), amely esetben a oszcillációs egységet nevezzük konzervatív kezelése. Példák oszcilláló linkek 19. ábrán látható módon. 19. ábra. Példák oszcilláló linkektovábbi anyagok