Számoljuk meg a koncepció

Síkgráfok. Euler formula.

Tekintsük a gráf kép G. 34. ábra ábrázolja egy grafikon G, néhány széleit annak újbóli metszik egymást. A 35. ábra, az azonos G gráfot ábrázolja úgy, hogy annak az élei nem fedik át egymást.
A grafikon a 40. ábrán egy lapos ábrázolása a grafikon a 39. ábrán.

Fig.39 ábra. 40
Egy gráf sík, ha lehet levonni egy lapos síkban úgy, hogy nincs két bordája nem volt más közös pontja, eltekintve a közös vertex.
Példák a síkgráfok egyszerű ciklusok, fák, erdő.
Mivel a jellemzői a lapos ábrázolása a gráf TSB-fogalmát egy arc.
Él egy lakásban ábrázolása egy G gráf része a sík által határolt egyszerű ciklust, és nem tartalmazott a többi ciklus.
Mivel az arcok részének kell tekinteni a gépet fajok helyzetét „kívül” a lapos ábrázolása a gráf; arra korlátozódik, hogy a „belső” egyszerű ciklust, és nem tartalmaz egyéb ciklusokat. Ez a része a sík az úgynevezett „végtelen” arcát.

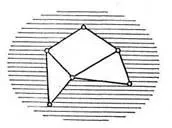
Ábra. 41
A 41. ábra része a végtelen arcok árnyékolt.
Fa és fa van az egyik oldala a végtelen.

Ábra. 42
Feladat 7.1. A 42. ábra egy sík ábrázolása egy gráf Add neki a szélén.
Válasz: (1, 7, 4, 1), (1, 3, 2, 4, 1), (1, 2, 3, 1), (2, 6, 5, 4, 2), (1, 2 , 6, 5, 4, 7, 1).
Miért rész-PFSZ-sík által határolt egyszerű ciklus (1, 2, 4, 1) nem etsya szélén?
Mert körülveszi a ciklus (1, 2, 3, 1).
Feladat 7.2.

Ábra. 43
Mi minden szempontjára grafikonon.
Válasz: (1, 2, 3, 4), (1, 2, 3, 4, 5, 1).
Miért része a sík által határolt egy egyszerű ciklus (1, 2, 3, 4, 5, 1), van egy arc?
Mivel a szélén (4, 5) belsejében található az arc nem alkot hurkot.
Feladat 7.3.

Ábra. 44
Része a sík, zashtri Hove 44. ábrán a szélén?
Válasz: Nem, mert nem egy ogre-nichena belsejében egy egyszerű ciklust.
Feladat 7.1.
Önkormányzat úgy döntött, hogy minden negyedévben a város, amelynek 155
csomópontok és az utcai szegmensek 260 közötti metszéspontok, szupermarket.
Hány lesz beépített szupermarketekben?
Határozat.
város térképe lehet tekinteni síkbeli gráf G, amelyben a csomópontok csomópontok és az utcai szegmensek - bordák.
Planar ábrán látható grafikonon adjuk. 45 három metszettel, ahol aspektus 1 - kívül, és az arcok 2 és 3 - a belső.

45. ábra
Tétel 10. Euler formula. Minden csatlakoztatott sík gráf egyenlet igaz: n-m + F = 2, száma gden- vershinm- élek számát, AF száma gráf élek.
Bizonyítás.
Részgráfja G, tartalmazza az összes a gráf nevezzük feszít®fája. Ha ostavny részgráf egy fa, ez az úgynevezett feszítőfa.
Tekintsünk egy feszítőfának Tgrafa G. Egyértelmű, hogy a grafikon Timeet n csúcsú egyik oldalán (a külső). Mivel a T - egy fa, az élek számát egyenlő T (n-1). Ezért a gróf Tdokazyvaemaya formula igaz. Most majd felváltva, de hozzá a hiányzó T szélei G. Amikor az egyes túlmenően a csúcsok száma söpör és az élek száma és az arcok növekszik a unit-nitsu. Ez azt jelenti, hogy a képlet bizonyított lesz igaz minden gráf hozzáadásával kapott műveleteinek bordák, és ezáltal az eredeti gráf. Ez azt bizonyítja, a tétel.
Mivel városrészek megfelelnek a belső felületei sík gráf, azt látjuk, az arcok száma Euler-formula. Egy gráf 155 csúcsa és 260 élek. A arcok száma benne: F = m - n + 2 = 260-155 + 2 = 107.
A város építeni 106 szupermarketekben.
Feladat 7.2.
A nyomtatott áramköri lemez egy lemez szigetelő anyagból, amelyben speciálisan gyártott foglalatok szerelt elektronikus eszközök. Mivel a vezetékek összekötő ezek az eszközök porlasztott fém síneket. Mivel a vezetékek nem elszigetelt, a pálya nem szabad átlépni. Ec-ha ez megtörténhet, hogy az egyik pályák át a másik száz Ron fórumon. Tervező Ivanov jött egy jó rendszer a nyomtatott áramköri lap, amely a 12 eszköz és 32 vezeték, connect-nek őket. Lehetséges, hogy egy ilyen díjat, hogy a vezetékek vannak elhelyezve az egyik oldalon?
Határozat.
PCB áramkör is képviselteti magát, mint egy grafikont, amelynek csúcsai képviseli buszos eszközök, és a széleket - vezetékek összekötő őket. A probléma megoldása csapódik le, hogy kérdés megválaszolása: Will G gráf, ábrázoló mérnöke Ivanov lapos?
Lássuk be az alábbi összefüggést: Proposition 3: egy csatlakoztatott lapos gras-fa, soderzhaschegonvershin imreber, N. 3-végrehajtott egyenlőtlenség stvom. 3n- 6.
Bizonyítás. Legyen G1, G2, ..., Ff- határán a G gráf, és m1, m2. MF ez korlátozza az élek számát, illetve az egyes arcát. Keresse meg az összeget az S = m1 + m2 +. + Mf.
Mivel minden egyes arc a gráf határolja legalább három bordát, a 3f. S. Másrészt, minden él tartozik, vagy két arcok vagy egyik oldalán, azaz a az összeg S kétszer vettük figyelembe, vagy egy. Ezért S. 2m. Eljutottunk 3f. 2m. Ezután használjuk a Euler formula:
f = m - n + 2,
3F = 3m - 3n + 6
2m? 3m - 3n + 6,
m. 3n - 6.
Az n = 3neravenstvo ellenőrzött közvetlenül.
Egyenlőtlenség bizonyult.
A G gráf, amely leírja a mérnöke Ivanova, n = 12, m = 32, és a fenti egyenlőtlenség nem teljesül.
Ezért gne gráf lapos, és egyoldalú nyuyu díj lehetetlen.
Feladat 7.3.
Engineer Ivanov (cm. Előző probléma) javította annak költségét. Most azt eszközök 9. és 17. a vezetékek (lásd áramkör. Ábra. 46). Lehetséges, hogy a hajón, hogy az összes vezeték idejű polgárok egyik oldalán?

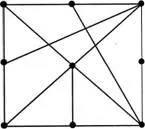
46. ​​ábra.
Határozat.
Feltesszük áramköri gráf egyenlőtlensége m. 3n - 6 nem tud válaszolni, hogy egy gráf G lapos, mint 17. * március 09-06 = 21.
Tekintsük a részgráfja G, vastag vonallal a 47. ábrán.

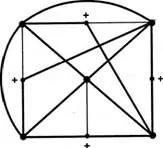
Ábra. 47
Ezt részgráf lehet beszerezni a teljes gráf öt csúcsok (C5) elhelyezése rá néhány-ryh bordái extra csúcsot. (Ábra K5vydeleny csúcsok, és a további csúcsok vannak címkézve „+” jel). Intro-kiegészítő csúcsok nem konvertálható nem-sík gráf K5 a lakásban. Ennélfogva, a G gráf, amelynek részgráf egy nem sík gráf is nem planáris. Ez azt jelenti, hogy készítsen egy oldalon a fórumon lehetetlen.
Ismert tétel struktúráját leíró síkgráfok. Azt ossza néhány széleinek grafikonok és K3,3 K5novymi csúcsok (lásd. Ábra. 48). A kapott grafikonok fogjuk nevezni, illetve grafikonok típusok K3,3 és K5.

Tétel 11.TeoremaPontryagina-Kuratowski (1927,1930 g). A grafikon lapos akkor és csak akkor, ha az nem tartalmaz részgráfok típusú K3,3 vagy K5.