Szélsőséges, a legmagasabb és a legalacsonyabb érték a funkciók

19. A helyi szélsőérték. Ennek szükséges feltétele fennállásának szélsőérték

Azt mondják, hogy ez a funkció vovnutrenneytochke oblastiDlokalny maximum (minimum), ha létezik egy okrestnosttochki

, minden egyes pontjaamely egyenlőtlenség

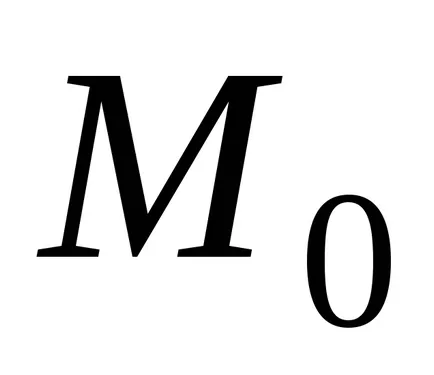
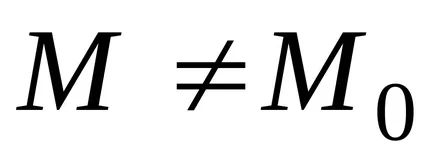
Ha a függvény egy pont

lokális maximumot vagy egy helyi minimum, akkor azt mondjuk, hogy az ebben a tochkelokalny extrém (vagy csak extrém érték).

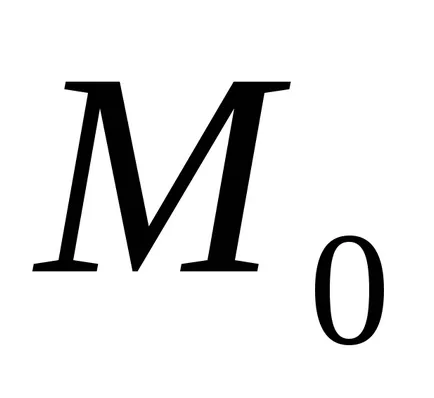
Tétel (szükséges feltétele extrémuma létezés). Ha differenciálható funktsiyadostigaet szélsőérték a ponton, mind az első, elsőrendű parciális derivált függvény

Ezen a ponton nulla.

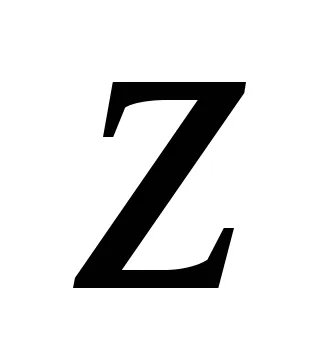
A pontok, ahol az összes elsőrendű parciális deriváltjai eltűnnek stacionárius pontokat hívott függvény. A koordináták Ezeknek a pontoknak megtalálható megoldásával rendszere

egyenletek

.

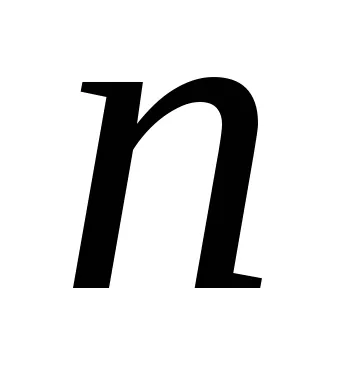
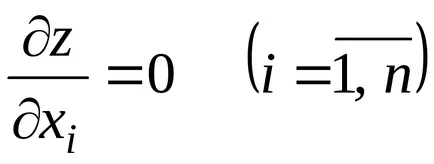
A szükséges feltétele a létezését szélsőérték esetében differenciálható függvény lehet röviden az alábbiak szerint történik:

.

Vannak olyan esetek, amelyekben az egyes pontok Részeredményeket származékok végtelen értéke van vagy nincs (a többi pedig nulla). Ezeket nevezik kritikus pontjai a funkciót. Ezek a pontok is figyelembe kell venni, mint a „gyanús” a szélsőséges érték statikus.

Ez a funkció a két változó szükséges feltétele a szélsőérték, vagyis a parciális deriváltak egyenlő nullával (eltérés) a extremális pont egy geometriai értelmezése: érintő sík felületén

Az extremális pont párhuzamos legyen sík.

20. Elegendő feltételek megléte szélsőérték

Performing egy bizonyos ponton a szükséges feltételeket a létezését szélsőérték nem garantálja a jelenléte a szélsőséges. Példaként vehetjük mindenütt differenciálható függvény

. Mindkét részleges származékai a funkciót is, és eltűnnek a ponton. Azonban minden szomszédságában ebben a kérdésben pozitív (nagyobb,) És negatív (kisebb) Értékei ezt a funkciót. Ezért ezen a ponton, definíció szerint, a szélsőérték figyelhető meg. Ezért szükséges, hogy ismerjük a megfelelő feltételeket, amelyek alapján az a pont, gyanús a szélsőérték egy szélsőérték a funkciót.

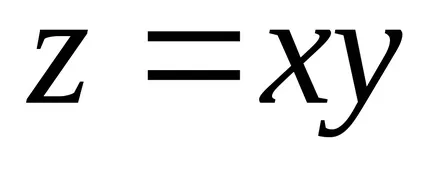
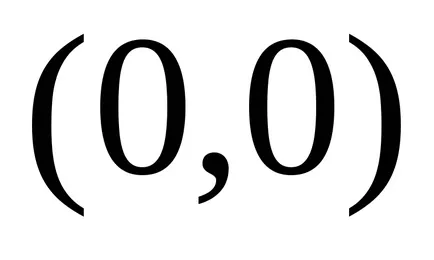
Vegyük azt az esetet függvényében két változó. Tegyük fel, hogy a függvény

Ez meghatározott, folyamatos és folytonos parciális származékok akár másodrendű közelében egy pont, amely egy stacionárius pont a függvény, azaz teljesíti a feltételeket

,

.

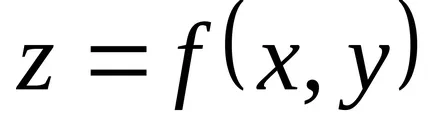
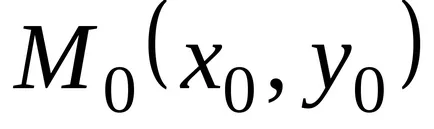
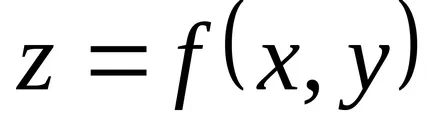
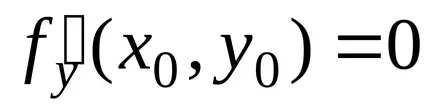
Tétel (elégséges feltételei extremum létezését). Legyen a függvény

Ez megfelel a fenti feltételeknek, vagyis differenciálható a szomszédságában egy fix pontés kétszer differenciálható pontnál. Akkor, ha

, majd tanult a függvénynek lokális szélsőérték,

akkor nincs extrémuma

hogy további kutatásokra van szükség.

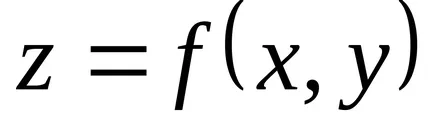
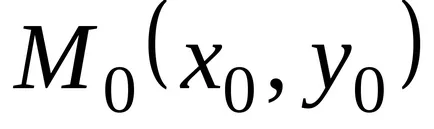
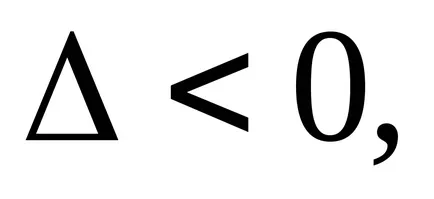
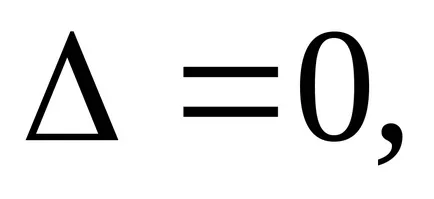
Abban az esetben,

a funkcióafolyásánál

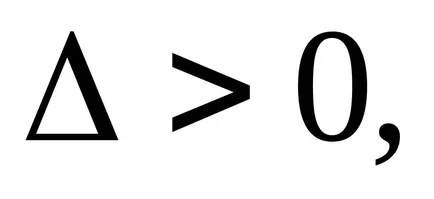
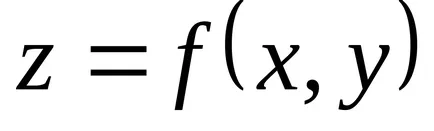
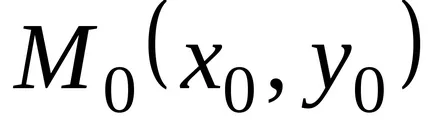
helyi maximuma

és

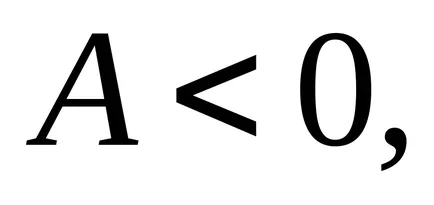
helyi minimuma

.

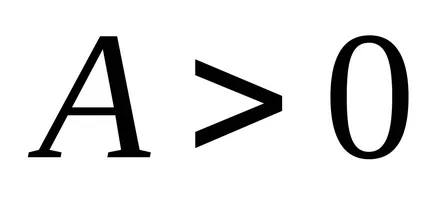
Általában elegendő a funkció a létezés tochkelokalnogominimuma (maximum) yavlyaetsyapolozhitelnaya (negatív) a második különbségi bizonyossággal.

Más szóval, a következő teljesül.

Tétel. Ha tochkedlya funkció

bármely nem nulla

, akkor ezen a ponton a funkció imeetminimum (analogichnomaksimum. Ha).

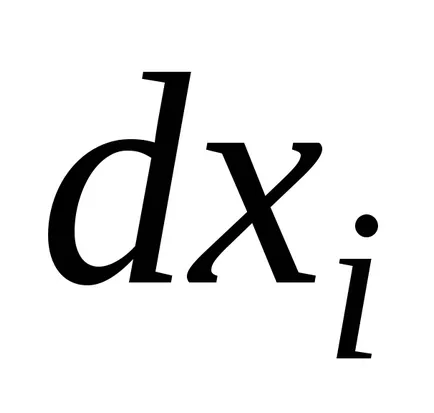
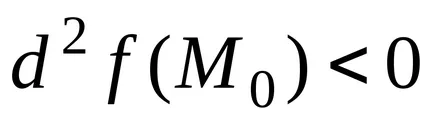
Példa 18.Nayti pont helyi szélsőérték

Határozat. Találunk parciális deriváltjai a funkció és egyenlőségjelet tesz a nullához:

Megoldása ezt a rendszert, azt látjuk, két pont a lehetséges szélsőérték:

Találunk másodrendű parciális deriváltak ezt a funkciót:

Az első helyhez pont, így iPoetomu hogy ezen a ponton további tanulmányozást igényel. a függvény értékét

Ezen a ponton nulla:további,

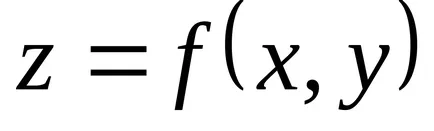
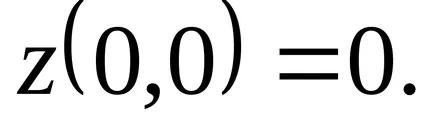
Következésképpen minden szomszédságában

függvényTart értékek nagy, és a kisebb, és ezért azon a ponton,függvény, definíció szerint, ha nincs helyi szélsőérték.

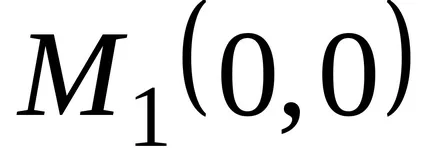
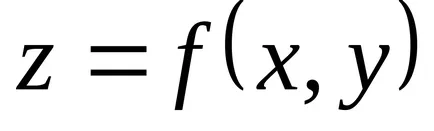
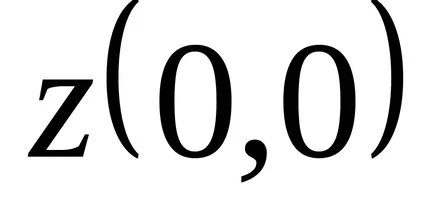
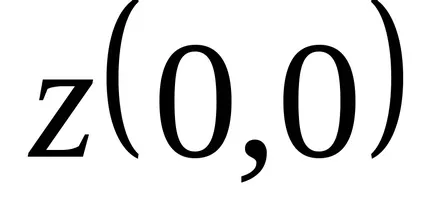
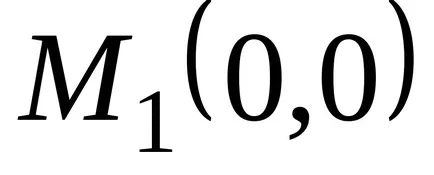
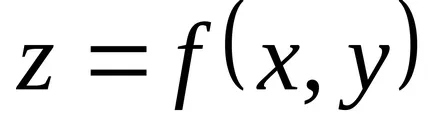
A második fixpontos

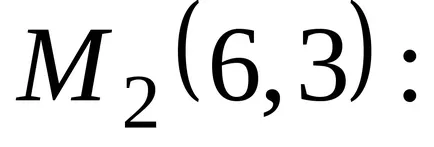
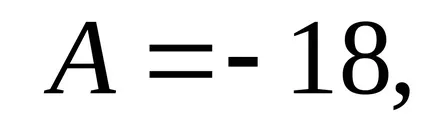
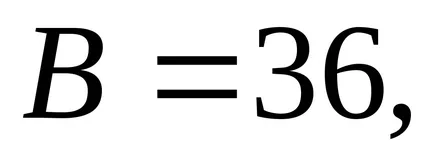
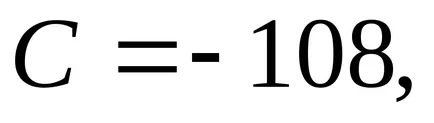
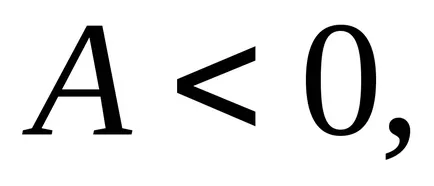
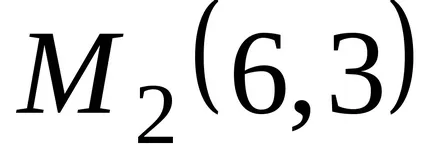
Következésképpen, ezért, mintpontnálfüggvény lokális maximuma van:

.