Személyes oldal - függvény y sin x, y cos x, y mf (x), y f (kx), y tg x, y ctg x

Ezután alkotunk egy grafikonon. Beszerzése félhullámú, a legmagasabb pontja, amely (π / 2; 1). Ez a grafikon a függvény az y = sin x intervallumban [0; π]. Hozzá ábrázolási szimmetrikus félhullámú (szimmetrikus az origó körül, azaz az intervallum -π). Ez a fél-hullám crest - egy X tengely és a (-1, -1). Az eredmény egy hullám. Ez a grafikon a függvény az y = sin x intervallumban [-π; π].

Akkor továbbra is hullám megszerkesztésével, és az intervallum [π; 3π], [π; 5π], [π; 7π] stb Mindezekben szegmensben függvény grafikonját ugyanúgy néz ki, mint az intervallum [-π; π]. Szerezzen be egy folytonos hullámos vonal van egyforma hullámok.

Grafikon egy szinuszhullám (gyakran nevezik koszinusz).

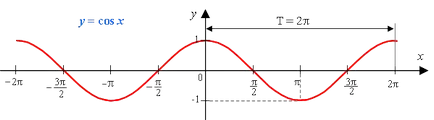
1) A domain a funkció - a valós számok halmaza.

2) területe függvény értékei - az intervallum [-1; 1]

3) Ez egy páros függvény.

4) Ez egy folytonos függvény.

5) koordinátáit a metszéspontok a grafikon:
- az abszcisszán: (π / 2 + πn; 0),
- az ordináta tengely: (0; 1).

6) A [0; π] működése csökken, az intervallum [π; 2π] - növekszik.

7) A időközönként [-π / 2 + 2πn; π / 2 + 2πn] függvény pozitív értékeket.
Időközönként [π / 2 + 2πn; 3π / 2 + 2πn] függvény értéke negatív.

8) A hiányosságok növelik: [-π + 2πn; 2πn].
Csökkenő intervallumok: [2πn; π + 2πn];

9) minimális pont: π + 2πn.
funkciója a maximális pont: 2πn.

10) Ez a funkció korlátos felett és alatt. A legkisebb függvény értéke -1,
1, a legnagyobb értéket.

11) Ez egy periodikus függvény egy időszak 2π (T = 2π)

Vegyük az előző függvény y = cos x. Mint már tudjuk, a grafikon egy szinuszhullám. Ha megszorozzuk a koszinusz függvény egy bizonyos számú m, akkor a hullám meghosszabbítja az X tengellyel (vagy csökken, attól függően, hogy az értéke m).
Ez az új hullám és lesz a grafikon y = mf (x), ahol m - a tetszőleges valós szám.

Így, az y = mf (x) - ismerős számunkra függvényében y = f (x), szorozva m.

Művészet nyújtás vagy tömörítés, akkor először építeni csak egy fél hullám szinuszos, majd befejezni az egész menetrend.

Ha a függvény az y = mf (x) vezet stretching a szinuszgörbe X tengely vagy x-tengely a tömörítés. az y = f (kx) vezet megnyúlását y-tengely, vagy a kompressziós y tengelyre.

És k - bármilyen valós szám.

A menetrend ezt a funkciót, akkor először építeni egy félhullámú szinusz, majd fejezze be a teljes menetrend.

A grafikon a függvény az y = tg x IS tangensoida.

Elegendő megépíteni a grafikon tartományban 0 és n / 2, akkor továbbra is szimmetrikusan az intervallum 0 3π / 2.

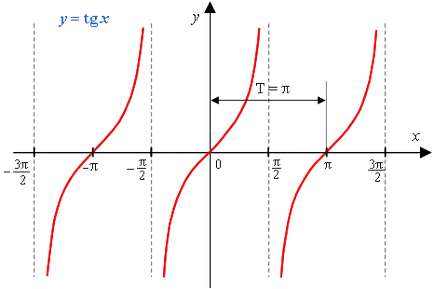
1) A domain a funkció - a készlet minden valós számok, kivéve a számok formájában
X = π / 2 + πk, ahol k - bármilyen egész szám.

Ez azt jelenti, hogy a gráf funkció nem a pont tartozó egy egyenes vonal x = π / 2,
egyenes vagy X = 3π / 2, vagy közvetlen x = 5π / 2, vagy közvetlen x = -π / 2, stb

2) Terület függvény értékek (-∞; + ∞)

3) Ezt a páratlan funkció.

4) Ez egy folytonos függvény felett intervallum (-π / 2; π / 2).

5) Ez egy periodikus függvény egy alapperiódusú π (T = π)

6) A nő az intervallum (-π / 2; π / 2).

7) Ez a funkció nem korlátozódik sem a felső vagy alsó. Azt sem a legkevésbé sem a legnagyobb értékeket.

A grafikon a függvény y = CTG x is tangensoida (néha kotangensoidoy).

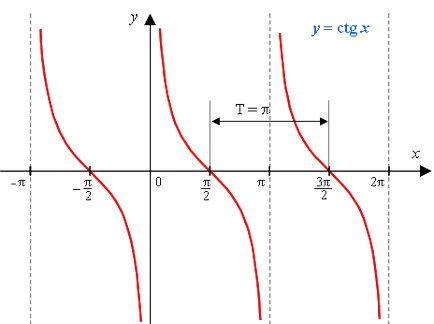
1) A domain a funkció - a készlet minden valós számok, kivéve a számok formájában
X = πk, ahol k - bármilyen egész szám.

2) Terület függvény értékek (-∞; + ∞)

3) Ezt a páratlan funkció.

4) Ez egy folytonos függvény.

5) Ez egy periodikus függvény egy alapperiódusú π (T = π)

6) működése csökken a rés (πk; π + πk), ahol k - bármilyen egész szám.

7) Ez a funkció nem korlátozódik sem a felső vagy alsó. Azt sem a legkevésbé sem a legnagyobb értékeket.