Személyes oldal - páros és páratlan függvények

Páros és páratlan funkciókat. periodikus függvények

Még egy olyan funkció, amelynek előjele nem változik, ha x jelet.

Más szavakkal, bármely x értéknél, a egyenlőség F (-x) = f (x). X jel nem befolyásolja a jele y.

Ütemezése még funkciót szimmetrikus a tengelyek (1. ábra).

Példák még funkciók:

Magyarázat:
Tekintsük az y = x 2 vagy y = -x 2.
Bármelyik értéke x olyan pozitív funkciót. X jel nem befolyásolja a jele y. A grafikon szimmetrikus a koordinátatengelyek. Ez még funkciót.

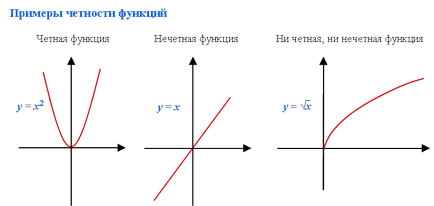
Páratlan függvénye, amelynek előjele változik az x jelet.

Más szavakkal, bármely x értéknél, a egyenlőség F (-x) = -f (x).

Graph páratlan függvény szimmetrikus az eredetét (2. ábra).

Példák páratlan funkció:

Vegyünk egy függvény az y = -x 3.
Minden érték lesz negatív. Ez a jele x befolyásolja a jele y. Ha a független változó - pozitív szám, és a pozitív funkciót, ha a független változó - egy negatív szám, akkor a negatív függvény: F (-x) = -f (x).
Ütemezés funkció szimmetrikus az eredetét. Ez egy páratlan függvény.

A tulajdonságok páros és páratlan funkciók:

1) összege akár funkciók még funkciót.
Az összeget a páratlan függvény páratlan függvény.

2) Ha az f függvény is, akkor a függvény 1 / f még.
Ha f páratlan, akkor a függvény 1 / f páratlan.

3) A termék a két, még funkciót páros funkció.
A termék két páratlan funkciók még funkciója is van.

4) A terméket az egyenletes és egy páratlan függvény páratlan funkciót.

5) A származékot egy még funkció páratlan, és a páratlan - még.

Nem minden funkció páros vagy páratlan. Vannak funkciók, amelyek nem tartoznak az ilyen fokozatosság. Például, a gyökér a függvény az y = √h nem tartozik egy még nem is páratlan funkció (3. ábra). Amikor felsorolja a tulajdonságait ezeket a funkciókat kell adni megfelelő leírását: minden páros, vagy páratlan.

Mint tudja, a frekvencia - az ismételhetőség bizonyos folyamatok egy bizonyos intervallumban. Leíró függvények ezeket a folyamatokat nevezzük időszakos feladatokat. Azaz, úgy működik, amelynek grafikonok elemek ismétlődő bizonyos számszerű időközönként.