Találjanak minimális előre meghatározott célfüggvény
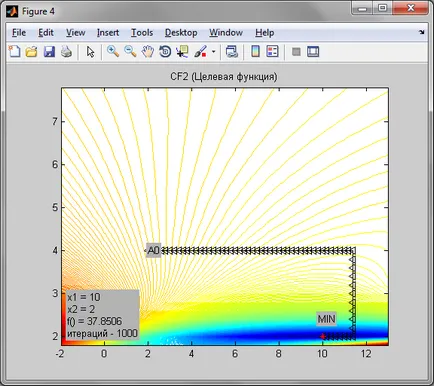
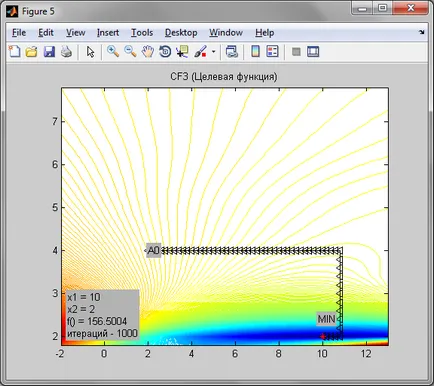
Tekintettel arra, hogy az eljárás a zéró nagyságrendű származású, ez elég pontos. Tekintettel arra, hogy a Rosenbrock funkció szakadékba enyhülést elérni a minimális pontot sikerült. megállási pont ebben az esetben elég messze a minimális pontot. Abban az esetben, a minimális pont ellipszis funkciót értünk el 21 iterációs lépésben h = 0,2. Annak ellenére, hogy ez a minimális ponton előre meghatározott célfüggvény született pontosan 91 per iterációs, a h lépés = 0,2, és a pontossága 0,0001.
bibliográfia
A projekt fő fájlt.
4. ITERATION_AMOUNT = 1000;
5. EPSILON = 0,001; % Pontosság
7. POINT_AMOUNT = 50; % Pontok száma
9% kiindulási pont
11. x_point_Ellipse (1) = 2;
12. x_point_Ellipse (2) = -2;
14. x_point_Rosenbrock (1) = 4;
15. x_point_Rosenbrock (2) = 3;
17. a1_T_point_CF (1) = 2;
18. a1_T_point_CF (2) = 4;
20.% a és b - az értékeket a sugarak F-II. Ellipszis.
24% kiindulási beállítások funkciót W (k).
28. ELLIPSE = 'ellipszis';
29. Rosenbrock = 'Rosenbrock';
32. rész 1% Euler.
33. y_teor = FirstPart_EulerMethod (a1, T, POINT_AMOUNT);
35% 2. rész coordinatewise optimalizálás.
36.% funkciót [value_of_funct, X] = SecondPart_OptimizationCoordinate (függvény_neve, h, epszilon, ITERATION_AMOUNT, a, b, y_exp, number_y_exp, POINT_AMOUNT)
37. [y_Ellipse, x_Ellipse] = SecondPart_OptimizationCoordinate (ellipszis, h, epszilon, ITERATION_AMOUNT, x_point_Ellipse, a, b, -1, -1, POINT_AMOUNT);
38. [y_Rosenbrock, x_Rosenbrock] = SecondPart_OptimizationCoordinate (Rosenbrock, h, epszilon, ITERATION_AMOUNT, x_point_Rosenbrock, a, b, -1, -1, POINT_AMOUNT);
40% 3. rész RNG. CF
41. [CF, a1_T_1, a1_T_2, a1_T_3] = ThirdPart (CF_text, h, epszilon, ITERATION_AMOUNT, a1_T_point_CF, a, b, y_teor, POINT_AMOUNT);
A funkció a Euler módszer.
1. funkció y_Euler_50point = FirstPart_EulerMethod (a1, T, POINT_AMOUNT)
3. globális y_Euler;
5. ITERATION_AMOUNT = 300; % A pontok száma az első menetrend.
6. x_t = 5; % Az állandó hivatkozási x (t)
11. coeff_z1 = 120 * a1 / T. ^ 2 + 6;
12. coeff_z2 = 6 * a1-120 + 48 * a1 / T;
13. coeff_x_t = 120 * a1 / T. ^ 2;
14.% free_term - szabad távon.
15. free_term = coeff_x_t * x_t;
17. i = 1: ITERATION_AMOUNT
18. z1 (i + 1) = z1 (i) + h * z2 (i);
19. z2 (i + 1) = z2 (i) + h * (x_t-z1 (i) -0.4 * T * z2 (i)) / T. ^ 2;
20. y_Euler (i) = coeff_z1 * z1 (i) + coeff_z2 * z2 (i) - free_term;
24.% i = 1: ITERATION_AMOUNT;
26.% cím (”. Y gráf elméleti pontok 300' );
28.% saveas (GCF, 'output', 'bmp');
29% -át a tartalék 300 pontok mindössze 50 (POINT_AMOUNT)
31. step_cycle = ITERATION_AMOUNT / POINT_AMOUNT;
32. i = 1: step_cycle: ITERATION_AMOUNT
33. y_Euler_50point (j) = y_Euler (i);
38.% i = 1: POINT_AMOUNT;
40.% cím ( 'Y elméleti grafikon 50 pont (minden 6).');
Funkció optimalizálás coordinatewise
1. rész 2% coordinatewise optimalizálás.
2. funkció [value_of_funct, X] = SecondPart_OptimizationCoordinate (függvény_neve, h, epszilon, ITERATION_AMOUNT, x_start_point, a, b, y_exp, number_y_exp, POINT_AMOUNT)
8. tiszta (varlist);
14. Mozgás%. hogy kihagyja a vizsgálati feltételeket ki dok. value_of_funct perc az utolsó három, vagy sem.
15. change_coord = 1;
16%, hogy kilépjen a hurok, ha a gróf. Több ismétléseket ITERATION_AMOUNT.
17. number_iteration = 1;
23. X (1,1) = x_start_point (1); % Első koordinálja, az első érték.
24. X (2,1) = x_start_point (2); % Második koordináta, az első érték.
25. X (1,2) = x (a változás, i-1) + H; % Első koordinálja, a második érték.
26. X (2,2) = x (konstans, i-1); % Második koordináta, a második érték.
28. value_of_funct (1) = Ellipse_Rosenbrock_or_CF (function_name, x (1,1), x (2,1), a, b, y_exp, number_y_exp, POINT_AMOUNT);
29. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, x (1,2), X (2,2), a, b, y_exp, number_y_exp, POINT_AMOUNT);
31. Ha new_value_of_function> value_of_funct (1)
33. X (1,2) = x (a változás, i-1) + H;
34. value_of_funct (2) = Ellipse_Rosenbrock_or_CF (function_name, X (változás, i), X (konstans, i), a, b, y_exp, number_y_exp, POINT_AMOUNT);
37. value_of_funct (2) = new_value_of_function;
40% a ciklust a modulusa a különbség funkciók nagyobb pontosság epszilon és az iterációk számát kevesebb, mint ITERATION_AMOUNT (10000).
41. míg (abs (value_of_funct (i) -value_of_funct (i-1))> Epsilon (number_iteration 43. number_iteration = number_iteration + 1; 45. change_coord = change_coord + 1; 47% hozzá a lépést, hogy az első koordináta. 48. X (változás, i) = x (a változás, i-1) + H; 49% második koordináta újraírása. 50. X (konstans, i) = x (konstans, i-1); 51% megtalálják a függvény értéke az új értékeket. 52. new_value_of_function = Ellipse_Rosenbrock_or_CF (function_name, X (1, i), X (2, i), a, b, y_exp, number_y_exp, POINT_AMOUNT); 54%, ha a funkció a pillanatnyi értékei több mint egy funkciót a korábbi, majd h = h * (-1). egyébként value_of_funct (i) = new_value_of_function. 55. Ha new_value_of_function> value_of_funct (i-1) 57% nullára ki az utolsó érték 58. X (változás, i) = NaN; 59. i = i - 1; % Visszatérés az előző minimális érték függvény % 62. Ha a sebességváltó pozíció tempójú készült nem kevesebb, mint 3 pontot, akkor azáltal, hogy min value_of_funct az utolsó 3. értékeket. 63. Ha (change_coord> = 3) 65%, ha a funkció az értékek az előző lépésben kevesebb a jelenlegi és a kevesebb, mint lépésben i-2, majd változtassa meg a koordináta-mozgást. 66. Ha value_of_funct (i-1)> = value_of_funct (i) 68. Miután Változás% koordináták ingerelt - zeroize change_coord. 69. change_coord = 0; 70. Ha (állandó == 1) 16. value_of_funct = sum ((y_exp (number_y_exp, :) - y_model) ^ 2) / POINT_AMOUNT ;. 20. value_of_funct = -1;