Tárgy 14_ekstremumy függvényében különböző változók
EXTREMA függvényében különböző változók
Szükséges attribútum ekstemuma.
Definíció: pont
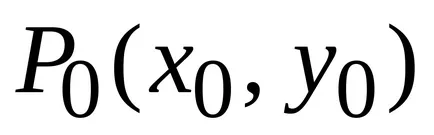
Létrehozza a kívánt szolgáltatást vagy állapot, amelyre a függvény elér egy olyan pontot
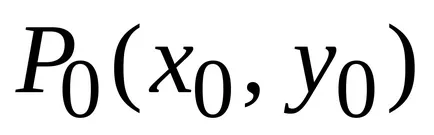
A szükséges kritérium extrémuma:
Ha a Z = f (x, y) differenciálható az x = x0. y = y0, és eléri a szélsőérték, majd ezen a ponton zérus részleges származékok:
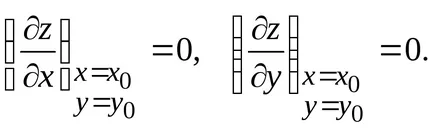
Tegyük fel, hogy z = f (x, y) van
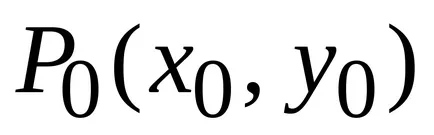
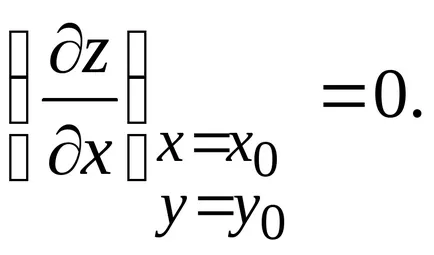
Hasonlóképpen, a Z = f (x, y) állandó x = x0. függvényében y. Ez eléri extrémuma meg y = y0. így
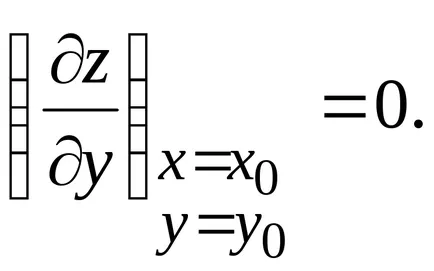
QED.
pont
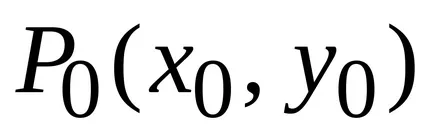
Az egyenlet a érintő sík felületén z = f (x, y)
helyhez kötött pont
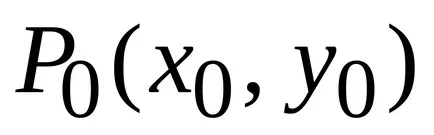
Ahhoz, hogy megtalálja a stacionárius pontok a Z = f (x, y) egyaránt egyenlő nullára annak parciális derivált
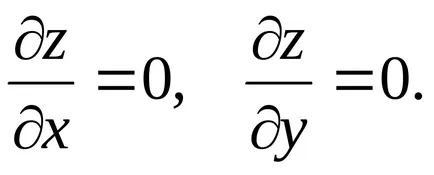
II.Dostatochnye körülmények szélsőséges. Hagyja, hogy a pont
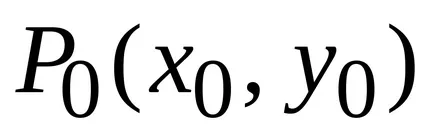
ha
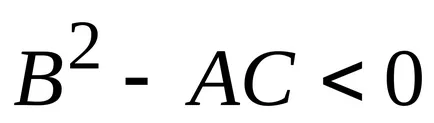
ha
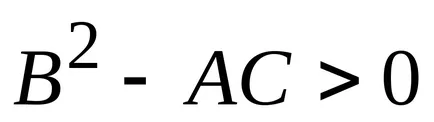
ha
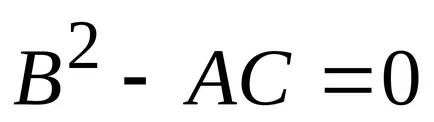
III.Pravila megtalálására szélsőségek.
Ahhoz, hogy megtalálja az extremális pontokat és extrém értékeket a Z = f (x, y) egy előre meghatározott régióban, szükség van:
1) egyenlővé részleges származékok nullára
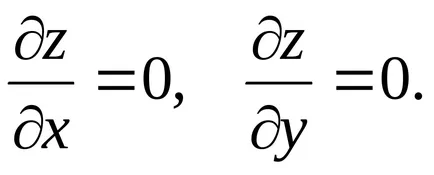
és megtalálja az igazi gyökereit rendszer két egyenlet. Minden pár gyökerek meghatároz egy rögzített pont a funkciót. Között a stacionárius pontok meg kell venni azokat, amelyek egy adott területen;
2), hogy kiszámolja a értéke expressziós
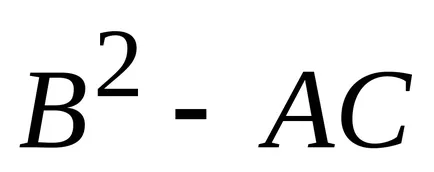
ahol mindegyik fixpont.
a) ha
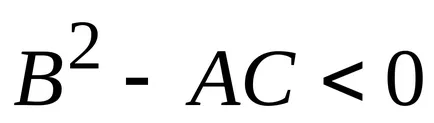
minimális az A> 0 (C> 0).
b) ha
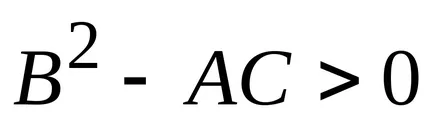
c) ha
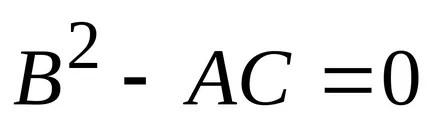
3) kiszámítja a szélső értékek helyett a függvénykifejezést koordinátáit szélsőérték pont.
IV.Naibolshee és minimális értékei a funkciót.
Tegyük fel, hogy szeretné megtalálni a maximális és minimális értékeket a függvény z = f (x, y) egy bizonyos régióban, úgy együtt határt.
Ha ezek közül bármelyik érték érhető el a területen belül működik, nyilvánvalóan szélsőséges. De előfordulhat, hogy a maximális vagy minimális érték a funkciót átveszi egy ponton feküdt a határt.
Ebből következik, e szabály alól:
annak érdekében, hogy megtalálják a maximális és minimális értékeket a függvény z = f (x, y) a zárt térségben, meg kell találni az összes maximumot vagy minimumot egy függvény belül kell elérni ezen a területen, valamint a legnagyobb vagy legkisebb függvény értékei a határait a területen. A legnagyobb az összes ezeket a számokat a kívánt értéket a legmagasabb és a legalacsonyabb - a legalacsonyabb.
Legyen egy Z = f (x, y) és a vonal L síkban 0xy. A kihívás az, hogy megtaláljuk a sorban L pont P (x, y). ahol az érték a Z = f (x, y) a legmagasabb, illetve a legalacsonyabb értékeivel összehasonlítva ez a funkció egy sor L. ilyen pontot nevezzük P pontok korlátozott optimalizálási Z = f (x, y) a vonalon L. Ezzel szemben, normális pont szélsőérték a függvény értékét azon a ponton, feltételes szélsőérték van az értékekhez képest, egyáltalán nem működik pont a környék, de csak azok, amelyek ellen a sorban L.
Nyilvánvaló, hogy a hagyományos szélsőérték pont és a pont korlátozott optimalizálási Bármely vonal áthalad ezen a ponton. De feltételes szélsőérték pont nem lehet a hagyományos szélsőérték pont.
Azt találjuk, extrémuma pont feltételes Z = f (x, y) a sorban a következő egyenlet adja L. (x, y) = 0. amely az úgynevezett egyenlet a kommunikáció.
Ha a kapcsolat az egyenlet fejezhető ki kifejezetten a y x. ezután helyettesítjük az egyenletben z = f (x, y). Kapunk z függvényében egyetlen változó:
Megtaláljuk az x értékét. amelynél a függvény értéke eléri egy szélsőérték, majd meghatározzuk a kényszer egyenletek megfelelő y értékei. megkapjuk a szükséges pontokat a feltételes szélsőérték.
Feladat feltételes szélsőérték probléma csökken megállapító szélsőérték függvény egy változó, és ha a kényszer egyenlet adja paraméteres egyenletek:
Ha a kényszer egyenlet bonyolultabb, és nem lehet egyértelműen kifejezni egy változót a másik felett, a probléma megtalálni a feltételes szélsőérték nehezebbé válik.
Mi írjuk a teljes függvény deriváltját z = f (x, y) az x
A feltételes szélsőérték pont a teljes származék nullának kell lennie. Ezen túlmenően, a változók, és meg kell felelniük a kényszer egyenletet. Így a probléma megoldása csökkenti a rendszer két egyenlet a két ismeretlenes
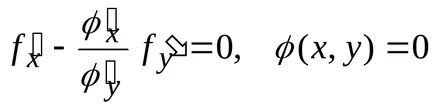
Mi átalakítani az első egyenlet formájában
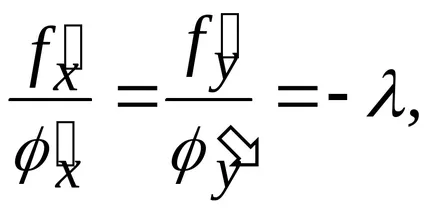
ahol - valós szám. Aztán jön a három egyenlet
az ismeretlen x. y. .
Egyenleteket (1) könnyebben megjegyezhető segítségével az alábbi szabályokat:
annak érdekében, hogy megtalálják pontokat, hogy lehet Feltételes szélsőérték pont a Z = f (x, y) a kommunikációs egyenletben (x, y) = 0. Meg kell alkotni a kisegítő funkciót
ahol = const és felállított egyenletek megtalálására szélső pontjait ezt a funkciót.
A fenti módszer problémák megoldására az úgynevezett Lagrange szorzók módszere.
A rendszer (1) csak akkor nyújt a szükséges feltételeket extrémuma. Nem minden pár x és y (1) van egy pont korlátozott optimalizálási.