Természetes számok, egyenlet

Feladat. A bal oldali csésze súlyok görögdinnye és egy 2 kg-os, és a jobb oldali csésze - súlya 5 kg. Mérlegek egyensúlyi állapotban vannak (ábra. 37). Mi a tömege egy görögdinnye?

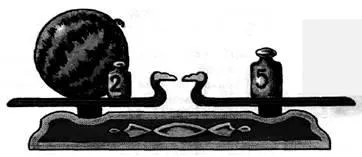
Ábra. 37. A mérleg egyensúly

Határozat. Jelöljük az ismeretlen tömegű görögdinnye a levél x. Mivel a mérleg egyensúlyban van, a egyenlőség x + 2 = 5.

Meg kell találni a az x értékét. amelyeknél az egyenlőséget. Belül a jelentése ennek kivonás érték a különbség a számok a 2. és 5., azaz 3. Ennélfogva, görögdinnye súlya 3 kg. Írása: X = 3.

Ha egyenlőség magában a levélben, az egyenlet igaz lehet néhány érték a betűk és rossz annak más jelentése.

Például, az x + 2 = 5 érvényes x = 3, és ha x értéke hamis = 4.

Az egyenlet az úgynevezett egyenlet tartalmazó levelet, amelynek értéke kell találni.

A betűk, ahol az egyenlet nyerik a megfelelő numerikus egyenlőség, az úgynevezett gyökér az egyenlet. (Például, a gyökér az egyenlet x + 2 = 5 van a 3-as szám)

Oldjuk meg az egyenletet - ez azt jelenti, hogy megtalálja az összes gyökerei (vagy győződjön meg arról, hogy ez az egyenlet nem rendelkezik egyetlen root).

1. példa Nézzük megoldja az x + 12 = 78.

Határozat. Értelmében a kivonás ismeretlen kifejezés megegyezik az összege közötti különbség, a másik kifejezést.

Ezért x = 78 - 12, azaz x = 66.

A szám 66 a gyökere az x + 12 = 78, mert 66 + 12 = 78 (ábra. 38).

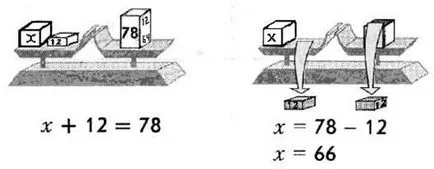
Ábra. 38. mérlegek és egyenlet

Ahhoz, hogy megtalálja egy ismeretlen kifejezés, meg kell, hogy vonja le az összeget a jól ismert kifejezés (ábra. 40 is).

2. példa Nézzük megoldani az egyenletet y - 8 = 11 (ábra. 39).

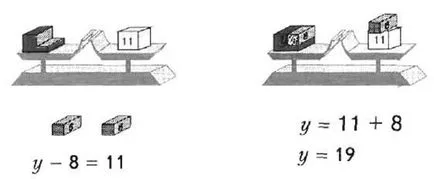
Ábra. 39. Egyensúly és egyenletek

Határozat. Kivonva a jelentését, a számok összege 11 és 8. Ezután, y = 11 + 8, azaz y = 19.

A 19-es szám a gyökere az egyenlet y - 8 = 11, mivel a egyenlőség 19 - 8 = 11.

Ahhoz, hogy megtalálja az ismeretlen csökken, akkor meg kell állapítani a kivonandó és a különbség (ábra. 40, b).

Ábra. 40. A egyenletek megoldása

3. példa Nézzük megoldani a 15 egyenlet - Z = 9.

Határozat. Kivonunk értelmében szám 15 az összege Z és 9, vagyis a z + 9 = 15. Ebből az egyenletből az ismeretlen távon: Z = 15-9, vagyis a z = 6

6-os szám a gyökér 15 - a Z = 9, mivel a egyenlőség 15 - 6 = 9.

Ahhoz, hogy megtalálja az ismeretlen kivonjuk, szükséges, hogy kivonja a redukált (ábra. 40, c).

Olvasásakor egyenletek és algebrai kifejezéseket, ne feledje, hogy a nevét, a betűk x, y, z hímnemű, és a nevét a többi latin betűkkel semleges.

Vail nevét a betűk matematika nem elfogadott.

x + 25 = 50 - összege X és egyenlő huszonöt és ötven;

X = 25 - X egyenlő huszonöt;

p - 18 = 20 - pH különbség húsz és tizennyolc;

p = 38 - pH egyenlő Harmincnyolc.

Német tudós Karl Gauss (ábra. 41) az úgynevezett király matematikusok. A matematikai tehetsége már gyermekkorában nyilvánvalóvá. Azt mondják, hogy a három év lepte mások, beállítja számításához apa és kőművesek. Egy nap az iskolában (Gauss akkoriban 10 év) tanár azt az osztályt, hogy összeadjuk a számokat 1-től 100-ig Miközben diktálta a feladat Gauss kész volt válaszolni. Az ő táblára írták: 101 × 50 = 5050.

Ábra. 41. Karl Gauss (1777-1855)

Próbáld ki magad, kitalálni, mint Carl Gauss hozzáteszi szám 1-100.

Ma már szinte minden nemzet fiók tucat, több száz, több ezer, ez egy tízes számrendszerben.

Ebben, mint már tudod, a számok értéke függ a helyét (pozíció), hogy úgy írni a számot. Ezért az ilyen számozási rendszer úgynevezett pozicionális.

Korábban egyesek használt egyéb számlák a rendszerben. A meleg afrikai országban és Amerikában, ahol az emberek mezítláb járnak, hogy a számla nem csak az ujjak, de a lábujjak. Nyert húszas.

De ötezer évvel ezelőtt néhány keleti országokban használták a hatvanas számrendszer, azaz radix 60. Ez a rendszer volt az első helymeghatározó rendszer.

Ábra. 42 azt mutatja, hogy a rendszer volt, mint egy rekord számokat.

Ábra. 42. A felvétel egyes számok a hatvanas rendszer számozása az ókori Kelet

Nyomokban hatvanas továbbra is: most osztják az óra 60 percre, és egy perc - 60 másodperc.

A 10-es számú, mint egy radix annak a ténynek köszönhető, hogy az emberek a kezüket 10 ujjal, hogy a legjobb, ha használhatók a pontszámot. De radix természetesen bármilyen szám lehet. Például a modern számítógépek (elektronikus számítógépek) úgy gondolja, hogy bináris (2-es alapú), mivel ebben az esetben csak két állam: „van egy jel” és a „nincs jel”.