Tétel az erőviszonyok és a módszer a bomlását erők komponenseket

elméleti mechanika

Tétel az egyensúlyi sík rendszer három nem párhuzamos erők

Tétel egyensúlyi síkjából rendszer három nem párhuzamos erők az alábbiak szerint történik: az egyensúlyi síkjából rendszer három nem párhuzamos erők szükséges, de nem elég, hogy a vonal ezen erők hatására metszik egy ponton.
Próbáljuk bizonyítani ezt az állítást, és miért a megállapított feltételek a tétel nem elegendő az erőviszonyok rendszert.

Tegyük fel, hogy három erő P. Q és F fekszenek egy síkban, a hatóirányának erők P és Q pontban metszik egymást A.
A vizsgálat alapján a III és IV axiómák statikus transzfer az erők P és Q vonalak mentén cselekvési A. pontban alapján axiómából paralelogramma találni nagysága ezen erők eredője FΣ.
Ennek eredményeképpen kapunk egy rendszer két erő - FΣ és F. amely egyenértékű az eredeti rendszer három erő.
De szerint Axiom III, egyensúly csak akkor lehetséges, ha az erők FΣ és F fekszenek egy egyenesen és irányított ellentétes irányban, ami azt jelenti, hogy a hatóirányának erő F. tartozó eredeti rendszer a három erő is, át kell haladnia A pont .
Ez azt bizonyítja, a tétel.

Ez a tétel azt mutatja, csak a szükséges az egyensúlyi állapotot, amely nem elegendő, mert a három erők közelednek egy ponton, de nem lehetnek egyensúlyban, ha a vektor nem nulla.

Force akció vonalak, amelyek metszik egy ponton, az úgynevezett konvergens.

Bomlása erő két komponensre

Bontjuk alkotmányozó hatalom -, hogy megtaláljuk a rendszer erők, ami megegyezik az erő. Általában, a munkacsoport bomlás két komponensre van egy végtelen számú megoldást, mivel a szilárdságot - méretű vektor.

Ahhoz, hogy a feladat volt egy határozott döntést, akkor be kell állítani a két feltétel, mint irány vagy modulok két részből áll. Négy lehetőség van FΣ expanziós erő két részre P és Q. alkalmazott ugyanazon a ponton. Minden esetben a döntés jön le, hogy az építőiparban a paralelogramma erők.

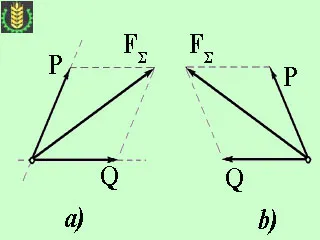
1. Vannak olyan területek két komponensből P és Q (a) ábra.
Ebben az esetben, az előre meghatározott irányban az erők P és Q pontból az erő alkalmazása FΣ. akkor megépíteni a paralelogramma erők, figyelembe vektor FΣ ereje az átlós a paralelogramma.

2. ismert nagysága és iránya az egyik komponens.
Megoldás grafikus módszerrel, mint az első esetben csökkenti az építési paralelogramma; ahol az ismert nagyságát és irányát az egyik oldalán és átlók a paralelogramma (b ábra).

3. Ismert modulok két komponens P és Q (a iránya nem ismert).
A probléma megoldódott a bevágások, ahol a féknyereg a elején a erő vektor FΣ lefolytatott ív sugara egyenlő modulo egy komponenst (P vagy Q) mindkét oldalán FΣ vektor. majd a végén a vektor tartott FΣ ív sugara a második komponens mindkét oldalán FΣ vektor. ívek átkelőhelyeken a csúcsai a paralelogramma erők kívánatos.
A probléma ebben az esetben:

4. Ismert irányba komponenst és Q eleme a második egység P. A problémát oldja meg egy eljárás serif. Így a kezdetektől a vektor hajtjuk FΣ line formában az irányt a vektor komponense az erő, majd keresztül a végén a vektor hajtjuk FΣ vonal párhuzamos az első sorban. Továbbá, az elejétől a második vektor FΣ vonal készült serifs ív, amelynek sugara egyenlő a második ismert összetevő modulját.
A feladat lehet:

• az egyik megoldás, ha a távolság a párhuzamos vonalak épített megegyezik a hossza a erőkomponens modult képez (ebben az esetben a szög a vektorok között a P és Q jelentése megegyezik a 90 fok);
• két megoldás, ha a távolság a párhuzamos vonalak kisebb, mint a hossza az ismert komponense az erő modul;
• nincs megoldás, ha a távolság a párhuzamos vonalak nagyobb, mint az az erő komponens ismert modul.