Tudományos és módszertani alapjait a tanulmány területek síkidomok az általános iskolában, az alapjait az elmélet a tér

Alapjai az elmélet a tér

Tekintsük az alapvető rendelkezéseket az elmélet teret.

Kezdjük egy definíció terület egy sokszög. Egy egyszerű sokszög nevezzük egyszerű, zárt sokszög összhangban egy része sík által határolt azt. Csak azokat az egyszerű sokszögek, hívja őket rövid sokszög.

Definíció: Tekintsük a készlet M összes sokszög az euklideszi síkon. Azt mondják, hogy a mérés a beállított sokszögek helyet, ha meghatározott leképezési S. M> R +. megfelel a következő axiómák:

Ha sokszögek F és F 'jelentése azonos, akkor S (F) = S (F').

S (P0) = 1. ahol P0 - szögletes, épülő egység intervallum egy oldalon.

A pozitív szám S (F), vagy intézkedés nevezzük területe egy sokszög F, négyzet P0 - egység-négyszög, és axiómának 1, 2 és 3 - axiómák területmérés.

1. Tétel: (létezése és egyedisége): az euklideszi geometria mindig létezik leképezés S. M> R +. kielégíti az axiómák 1., 2. és 3. ha a kiválasztott intervallumon, akkor ez egy egyedi leképezés.

Hatás: A területének összege e háromszögek azonos bármilyen módszerrel F sokszög bontás véges háromszögek.

Megjegyzés: A létezése és egyedisége a terület egy sokszög nem bizonyított az iskolában geometria természetesen. Mindazonáltal, az elmélet a tér, tanítják az iskolákban, egy konkrét jelentése: ez alapján a követelés (ami elfogadott bizonyítás nélkül), hogy létezik egy leképezés S. M> R +. kielégítő axiómák 1., 2. és 3. lehetővé teszi, hogy kiszámítja a terület az elemi sokszögek néhány adatot, így az iskolában során geometriai elrendezését egyediségét intézkedés legegyszerűbb sokszög. Tegyük fel például, hogy területének kiszámítására egy sokszög F, mi törte háromszögek és vette a területek összegét a kapott háromszögek. Magától értetődik, hogy a különböző módon bontani háromszög megkapjuk ugyanazt az eredményt. De miért? Az iskolában geometria válasz erre a kérdésre: nem. Létezése és egyedisége tétel ad egyértelmű választ: bármely partíció a sokszög a háromszögek F a négyzetének összege ad egyedileg meghatározott számú S (F). E tételből, és a kimeneti terület az axiómája képlet területén minden téglalap, paralelogramma, háromszög.

2. Tétel: Ha S. M> R + - feltérképezése kielégítő axiómák 1, 2 és 3, S (p) = xy, ahol P - téglalap amelynek oldalai egyenlő x és y.

Tétel 3 Amennyiben S. M> R + - feltérképezése kielégítő axiómák 1, 2 és 3, S (T) = xy, ahol T - háromszög, X - egyik oldalán, és a y - megfelelő magasságban.

Definíció: Két sokszög nevezik izometrikus, ha a területek egyenlő.

Egyértelmű, hogy van egy azonos-ekvivalencia reláció a halmaz M minden sokszög.

Definíció: Két sokszög F és F „nevezik equidecomposable ha tudják bontani az azonos számú sokszög rendre egyenlő.

Belátható, hogy ez az arány equidecomposability is, egy ekvivalencia reláció a halmaz M minden sokszög.

4. tétel: Ha a sokszögek equi, azok egyenlő területet.

Megjegyzés: Ez a tétel alapul bomlási módszert kiszámításához a terület a sokszög F: a poligon van szétbontva véges halmaza poligonok, oly módon, hogy az egyik lehet „hajtogatott” egy sokszög, amelynek területe ismert. Ily módon egy iskolában során geometriai képletek kiszámításához területén paralelogramma, háromszög, trapéz.

A következő állítás inverze 4. tétel.

5. Tétel (Bolyai-Gervin): Ha a sokszögek egyenlő területű, ezek equi.

Így több M egyenlőség valamennyi poligonok aránya egybeesik equidecomposability arányt.

És mi a helyzet a térségben egy tetszőleges alakú, például, amelynek területe a kör? Ez a probléma merül fel, amikor a geometria a benyújtott anyag az iskola. Van egy bővíteni kell a vizsgálati területen terek elméletét, ami eddig csak a készlet minden sokszög síkjában.

Definíció: ábra M nevezzük Quadrature ha bármilyen pozitív szám lehet felvenni, mint sokszögek P és Q, hogy a P és M Q S (Q) -S (P).

6. Tétel: Az adathalmazt squarable létezik, és csak egy, az S függvény, kielégíti axiómák 1, 2 és 3. A mérési területek.

A száma S (F) nevezzük a terület a szám F, ahol F- squarable ábra.

Megjegyzés: A kalkuláció a terület a szám, a megfontoláson alapul, sokszögek, fokozatosan kitölti a teljes szám, az úgynevezett eljárás kimerültség (a tankönyvekben a módszer segítségével levezetjük a képlet területének egy kört, és nem csak).

Alkalmazásáról szóló raklapok (közvetlen mérés területek).

Ez általában azt mondta, hogy a terület S (F) az F a figurák száma jelzi, hogy hány egység terület a szám készült (a területegységre jutó vesszük négyzet, amelynek oldala hossza megegyezik egy). Azonban egy ilyen világos magyarázatot nem lehet pontos matematikai meghatározása a tér fogalmát. Nem világos például, hogy milyen egységekből áll a terület kör adott sugarú.

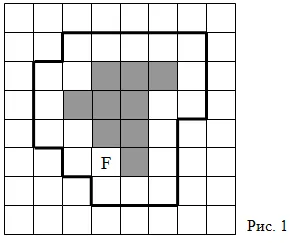
Az egyik módja, hogy meghatározzuk a koncepció a terület a megfontoláson alapul, paletta - partíció a síkból egybevágó négyzet. Hagyja, mozaik oldalán a tér van hossza 1: Legyen adott egy szám F és hagyja, hogy a1 a legnagyobb négyzetek számát, teljes mértékben tartalmazza az ábrán F és b1 - a legkisebb négyzetek számát tartalmazó ez a szám teljesen. Például, az ábrán F tartalmaz egy alak alkotja 9 négyzet mozaik és tartalmazta az ábrán, amely a 29 terek, azonban 9 # 63; S (F) # 63; 29, azaz a1 = 9, b1 = 29 (1. ábra).

A pontosabb értékelést is használható raklap, ami négyzetek oldalai hossza 1/10 (úgy, hogy minden téren 100 tartalmazza az előző mozaik négyzetek új mozaik). Ha, mondjuk, F tartalmaz egy figura alkotja 1 716 új terek mozaik és tartalmazott egy alak alkotja 1 925 ilyen négyzet, majd 17,16 # 63; S (F) # 63; 19.25. Ismét, köszörülés mozaik (azaz csökkenti a 10-szer a hossza az oldalán a négyzetek), akkor több, pontosan megbecsülni S (F), stb

Ismertetett mérési folyamat nem csak, hogy megtalálják a területen, hanem a terület meghatározása. Nevezetesen, úgy a mozaik, amelyben a hossza az oldalán a négyzetek egyenlő 1/10 k. Tegyük fel, hogy F tartalmaz egy alak alkotja négyzetek ak e mozaik és tartalmazott egy alak alkotja bk ilyen négyzetek (például, a fenti van a2 = 1716, b2 = 1925). Akkor azt mondhatjuk, hogy ak / 10 2k az értéke az ábrán F helyhiány és bk / 10 2k - bőségesen. Korlátlan növekvő k látjuk határain: (F) =. (F) =. amelyek közül az első az úgynevezett alsó, és a második - a felső részén az ábrán F.

Ha az alakja olyan, hogy ezek a határok egybeesnek. ez a szám F Quadrature, azaz (F) = (F). Ezt az értéket tekintettük a területen kívül az úgynevezett ábra F és jelöljük S (F), azaz

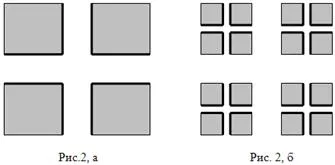
Ez könnyű, hogy egy példa a számadatok, amelyben a felső és alsó területen nem ugyanaz. Ebből a célból, a terület egy négyzet keresztmetszetű eltávolításához 1, amely terület kevesebb, mint 1/4 (2A.). Ezután mind a négy fennmaradó négyzetek törlendő a kereszt úgy, hogy az összeg a területek mind a négy keresztek kevesebb volt, mint 1/8 (2B.). Ezután távolítsa el a 16 keresztezés teljes területe kevesebb, mint 1/16, stb Ábra, amely marad eltávolítása után a végtelen számú keresztek, jelölje Q. Megjegyezzük, hogy a teljes terület összes távoli keresztezi kevesebb, mint 1/4 + 1/8 + 1/16 + ... + 1/2 n + ..., azaz kevesebb, mint 1/2.

Ezért, a fennmaradó ábrán Q nem lehet elhelyezni a területen az ábra 1/2, azaz, ábra Q felső területe nagyobb, mint 1/2. Ugyanakkor ez a szám a Q nem tartalmaz semmilyen téren (akármilyen kicsi lehet), és mivel az alsó területen a szám nulla. Így a felső és alsó részén az ábrán nem esnek egybe, és így a szám Q nekvadriruema.

Ez a példa azt mutatja, hogy a tér fogalmát nem alkalmazható bármely szám. Azonban lehet mutatni, hogy minden sokszög squarability figura. Hasonlóképpen, bármely konvex alakú (például kör) squarable. És általában az osztály squarable számok meglehetősen kiterjedt.

Most azt mondhatjuk, hogy a mérés S tér egy függvény a osztály valamennyi ábrát és squarable fogadó numerikus értékeket, azaz a Terület S (F) az egyes szám F egy nem negatív szám (az egységnyi felületre rögzítettnek tételezünk fel).

Ezt a definíciót terület (via paletok) bizonyítani tudja, számos olyan tulajdonsággal tér ...

Általánosságban meg kell jegyezni, hogy amikor raklap az iskolában hasznos megjegyezni a következőket:

Mérték területen keresztül mozaik közvetlen (azonnali) mérés, amelynek során a kívánt mennyiség értékét úgy határozzuk meg, hogy összehasonlítjuk azt a megfelelő egység. Terület mérés mérésével szegmensek hossza és egy közvetett képletek. Cseréje közvetlen összehasonlítása közvetett összehasonlítás jelentős eredmény az emberi gondolkodás és az egyik legrégibb matematikai absztrakciók. Nincs okunk azt feltételezni, hogy ez a kivételi könnyen adott hallgató, félreértés az a tény nagyban megnehezíti a további vizsgálatot az elmélet mérési területek (azaz a legkisebb négyzetes középértéke téglalap tanulmány képlet az esetben, ha a szélesség és hosszúság nem lehet kifejezni természetes számok). Miután az összes, mielőtt tudtam kiszámítani a szegmensek hossza bármely képletek tanítunk közvetlen mérés szegmensek, és ezáltal lehetőséget adnak a teszt számítás közvetlen mérésével. A téma „tér” ez elsődleges szakaszában pontosan megfelel dolgozni paletta.

A kurzus a geometria alapvető iskola zárt térben találni formák egyenes vonalú vagy kör kontúrok és részei. A gyakorlatban azonban, meg tud felelni az ábrán egy tetszőleges kontúr, és bosszantotta, hogy az alapvető iskola végzős nincs felkészülve a megoldás a megfelelő problémát.