Vereina l
= V ¥ mv + r ¥ MA = 0 + r ¥ F = M O.
Ha egy anyagi pont, több erők, M O kell tekinteni, mint egy pillanatát a kapott.
dL O dt = Â M iO.
amely kifejezi a tétel változásának perdület egy anyagi pont középpontjához viszonyítva:
az idő szerinti deriváltja a perdület vektor az anyag pont középvonalához képest megegyezik a geometriai összege pillanatokban a ható erők a pontot, viszonyítva ugyanabban a központban.
Az utóbbi függőség felírható előrejelzések a koordinátatengelyeken:
dl x dt = Â M ix; dl y dt = Â M IY; dl Z dt = Â M iz.
Ezek az egyenletek jelentik a tétel változásának perdület tengelye körül pont:
az idő szerinti deriváltja a perdület egy anyagi pont tengely körül egyenlő az algebrai összege a pillanatokban a ható erők pont tekintetében ugyanazon a tengelyen.
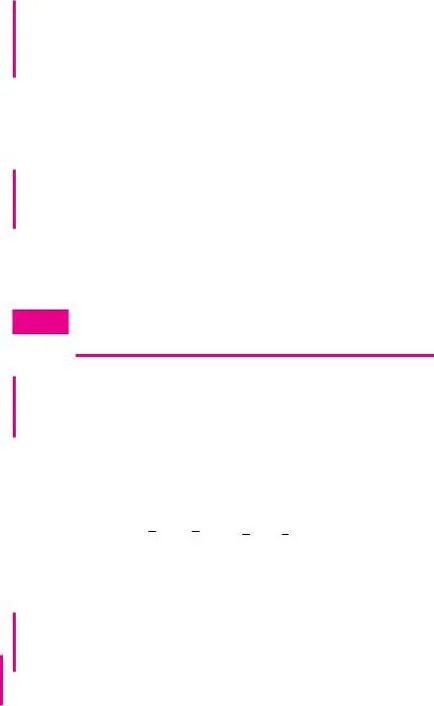
A következmény tétel. 1. Ha a hatóirányának a kapott ható erők az anyag minden alkalommal halad át egy bizonyos központ, a perdület egy anyagi pont állandó marad képest ebben a központban.
Ebben az esetben, a teljesítmény az F - mindig mentén irányul rádiuszvektorhoz a pont - -
Ki B (ábra 1,64, b.), ezért a vektor termék r - ¥ F
és ezért, L - C = const.
2. Ha a kapott pillanatban az alapanyagon pont erők egy tengely körül minden időpontban megegyezik a
nulla, a perdület egy anyagi pont A viszonylag a tengelyével állandó marad. nullával egyenlő, azaz a. e. a pillanatban F erő tekintetében a C pont nullával egyenlő,
Például, ha S M IV = 0, tehát, dl y / dt = 0 és y = L
1.20. Tétel AMEND kinetikus pillanatban mechanikai rendszerek
Kinetic perdület a mechanikai rendszer képest egy adott call center vektor egyenlő a mértani összege perdület az anyag pont a rendszer képest ez a központ.
A kinetikus perdület a mechanikai rendszer is nevezik a fő perdület a mechanikai rendszert. Például, tekintettel egy központ akkor kell kiszámítani a következők szerint:
L B = Â L iB = A (r i ¥ m i v i).
ahol r - - sugara vektor i-edik anyagi pont középpontjához képest a i; m i v - i - az összeget a mozgás egy anyagi pont.
A lendület a rendszer tengelyéhez viszonyítva egyenlő az algebrai összege perdület anyagi pont a rendszerben, tekintettel az azonos tengelyen.
Például, a tengelyhez képest Oz
Tekintsünk egy mechanikus rendszer, amely a k anyagi pont. Anyaga pontok mozgásban az intézkedés
egy külső F i E és F i J belső erők. Minden anyagi pont a kiválasztott fix középső O alapján a tétel változásának perdület write
d L io = M iO E + M iO J.
K megszerzéséhez egyenletek; összege:
 dt d L io =  M iO E + A M iO J.
Mint korábban leírtuk (lásd. Sect. 1,12), az összes belső elsődleges pillanatban erők bármilyen központ nullával egyenlő, azaz. E.
 M iO J = 0. Ekkor
 dt d L io =  M iO E vagy dt d  L io =  M iO E.
Ez az egyenlet egy tétel a változás a perdület mechanikai rendszer:
az idő szerinti deriváltja a perdület vektor képest mechanikus rendszer a központ a fő pillanatokban a ható külső erők a rendszer, viszonyítva ugyanabban a központban.
Vector egyenlőség mérkőzés három egyenlőség előrejelzések a koordinátatengelyeken:
dl x dt = M x E; dl y dt = M y E; dl z dt = M z E.
ahol L x. L y. L Z - kinetikus pillanatokban a mechanikai rendszert képest a koordinátatengelyek; M x E. M y E. M z E - a fő pillanatokban a ható külső erők a rendszer közel azonos tengelyek.
A következmény tétel. 1. Ha a fő pillanata külső erők tekintetében a központ minden alkalommal nulla, a perdület egy mechanikus rendszer tekintetében ez a központ állandó marad:
dl - O / dt = 0, és ezért L - O = const.
Ez a helyzet az úgynevezett megmaradási törvénye kinetichesko-
th pillanatra a közepén a mechanikus rendszer.
2. Ha a fő pillanatban a külső erők egy tengely körül minden alkalommal nulla, a perdület egy mechanikus rendszer tengelyéhez képest változatlan marad.
Például, M z = 0, akkor dl z / dt = 0, és ezért L Z = const.
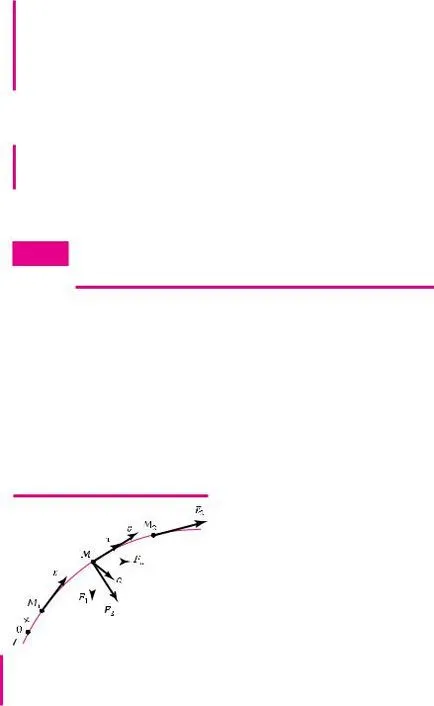
1.21. Tétel, hogy módosítsa a mozgási energiája anyagi pont
Természetesen a fizika ismert, hogy a kinetikus energia egy anyagi pont az m tömegű. mozgó v sebességgel -. felével egyenlő a termék a tömege ezen a ponton a tér a sebessége:
Nézzük meg a mozgás az M pont a kereset azokra alkalmazott rendszerek erők F - 1. F - 2. ..., F - N (ábra 1.65.). Válasszon pozitív irányba, a referencia és írjon a alapegyenletének dinamika
Itt az F erő - F kapott egy konvergens rendszer erők - 1. F - 2. ..., F - n. Mi a projekt a vektor egyenlő a T-tengely:

kapott érték tangenciális gyorsulás az egyenletben a mozgás mentén az egység vektor t -.
m v d v DS = F t és m v d v = F t dS. vagy d (m V 2 február) = fds cos (F. t).
A bal oldali ennek az egyenletnek a mozgási energia eltérés pont és a jobb oldalon - az elemi műveletet a kapott elmozdulás dS (műveletet végzi csak a tangenciális komponense eredő erő):
d (m V 2 február) = D A.
Mivel F t = F i t. és mozog a pont az erő alkalmazása egyáltalán azonos, hogy a d A = D A i. Ezért tudjuk írni a kinetikus energia eltérés más módon:
d (m V 2 február) = D A i,
t. e. kinetikus energia eltérés elemi pontok összegével egyenlő a munkálatok az erőknek a pontot.
Amikor mozgó pont M pont M helyzetbe sebessége v - v - február 1
Ez változhat 1 vagy 2; Ebben az esetben változtassa meg a kinetikus energia
m v 2 2 2 - m v 1 2 2 = D A i.
Az így kapott egyenlet a tétel a kinetikus energia változás anyagi pont:
a kinetikus energia az anyag változása szempontjából néhány elmozdulása megegyezik az algebrai összege munka minden aktív ezen a ponton az erők ugyanazon mozgásban.
Ha az összeg a munkaerő pozitív, akkor v 2> v 1 t. E. A mozgási energiája nő. Ha ugyanazt a mennyiségű munkát negatív, akkor a kinetikus energia csökken.
1.22. Differenciál egyenletek transzlációs mozgást SZILÁRD
Előrehaladó mozgás során egy merev test minden ponton mozog, valamint a tömegközéppontja, így a differenciálegyenletek a mozgás a súlypont leírják transzlációs mozgás a test:
Ahol m - tömege a merev test; x C. Y C. z C
Nia tömegközéppontja a test a koordinátatengelyeken; F ix E. F iy E. F iz E - vetülete a ható külső erők a merev test, a megfelelő tengelyekre.
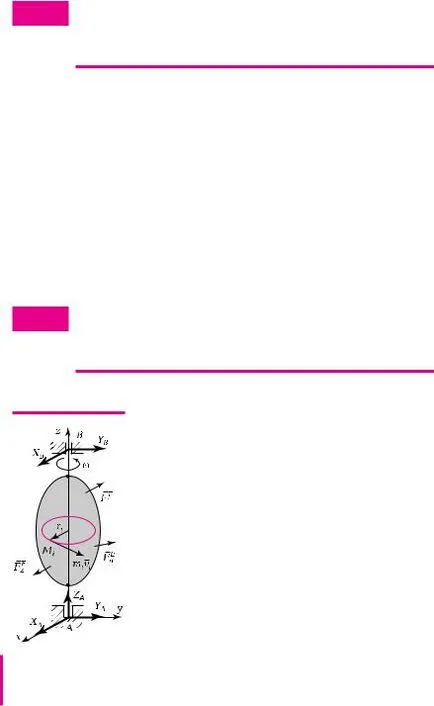
1.23. Differenciálegyenlet forgási mozgás egy merev test körül egy rögzített tengely
Szilárd test körül forog egy rögzített tengely körül az intézkedés alapján a külső erők F - i E (ábra 1.66.) Szögsebességgel w. A perdület tekintetében az A tengelyre z összegével egyenlő a perdület anyagi pontok tekintetében az azonos tengely, azaz. E.
L Z = Â m i v i r i = a m i w v i r i = a m i w r i 2 =
= W Â m i r i 2 = W J z.
Így kimutatták, hogy a kinetikus pillanatban egy forgó merev test viszonyítva rögzített tengely egyenlő a termék a tehetetlenségi nyomaték tekintetében azonos tengelyen szögsebességgel a test:

Összhangban a tétel változásának perdület tengelye körül az írási idő származékot a perdület tengelye körül Az
dl Z dt = Â M iz E vagy d (J z w) dt = Â M i E z.
J z d w dt = Â M iz E vagy J r e = Â M iz E.
Tekintettel arra, hogy a szöggyorsulással e második deriváltját képviseli a test forgási szöge j, a kapott kapcsolat lehet írva a következő:
J z j = Â M i E z.
Az eredmény egy differenciálegyenlet a forgómozgásának egy szilárd képest rögzített tengely. Meg kell jegyezni, hogy a jobb oldalon - ez az a fő pont külső előre meghatározott erő F i E. reakcióidő kötvények tengelyéhez képest Az nullával egyenlő, mivel a határokon reakciók Az tengely:
Ha a fő pillanatban a külső erők a forgástengely nulla, a perdület a rendszer állandó marad:
Ebben az esetben, ha a tehetetlenségi nyomatéka a rendszer változatlan, a rendszer forog egy állandó szögsebességgel. Ha megváltoztatjuk a tehetetlenségi nyomatéka, a szögsebesség is változik:
J z 1 w 1 = J Z 2 w 2.
1. Mi az abszolút szilárd test?
2. Milyen rendszereket erők megfelelője?
3. Mi az az elv oldható merev testet a kapcsolat?
4. Mi különbözteti meg az aktív és passzív erők?
5. Az úgynevezett sík vagy térbeli erőrendszer?
6. Mi a különbség összetartó erők önkényes helyen konjugált az űrben?
7. Milyen a nyomaték a lényeg?
8. Vedd alapegyenletei egyensúlya egy tetszőleges rendszer térbeli erők.
9. Mi a fő vektora erők és mi ő? Vajon az elsődleges vektora az erők a választott így a központ?
10. Sorolja meghatározására szolgáló módszerek súlyponthelyzet a merev test.
11. Van-e a gyorsulás anyagi pont egyenletes mozgás ívelt pályája?
12. Tud-e a pontokat a test, mozgó folyamatosan, hogy Cree volineynye pályáját?
13. Mi a pillanatnyi sebessége a közepén egy síkidom?
14. Ha az utas az utastérben a repülés irányában, a sebesség a Földhöz képest többé-Men Chez mint a repülőgép sebessége?
15. Mi a mozgás a test teszi a további két rotációs mozgások, amelyben a szögsebessége egy kovye és különböző irányokba?
16. Írja le a alaptörvényét dinamikáját.
17. Mi az a munka, a gravitációs erő? Függ attól, hogy milyen típusú pályán a pont az erő alkalmazása?
18. Határozza meg a hatékonyságot. Miért hogy ezt a koncepciót?
19. Hogyan kell meghatározni a súlypont a teherautó?
20. Határozza meg a mozgás mértékét a kerekek súly G és a sugár
R. gördülő egyenes vonalú vasúti csúszás nélkül szögsebességgel w.
21. bármilyen helyen, az összeg a mozgásvektor társ tömegpont pillanata a tengely körül lesz egyenlő nulla?
22. Milyen feltételek mellett a perdület a mechanikai ICU témák közepéhez képest változatlan marad?
23. Miért megállítani, gyorsan forgó korcsolyázó korcsolyázni dobott kéz a kézben?