1-0, 378 * (E
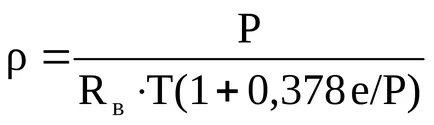
A mennyiség nazyvaetsyavirtualnoy hőmérséklet (Tv).
.
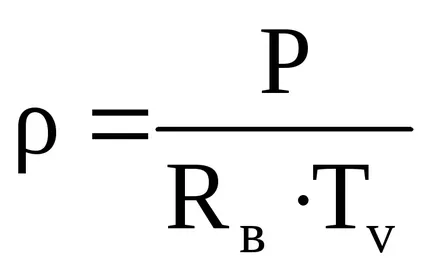
vagyis a sűrűsége nedves levegő által leírt állapotegyenlet száraz levegő, de a csere a T hőmérséklet, hogy egy virtuális hőmérsékleten Tv.
Virtuális nedves levegő hőmérséklete Tv - az a hőmérséklet, amelyen az, hogy száraz levegő sűrűsége egyenlő a sűrűsége nedves levegő hőmérséklet T. P nyomás és a vízgőz nyomása e.
A virtuális hőmérséklet mindig valamivel magasabb, mint az igazi hőmérséklete a nedves levegő.
a levegő sűrűsége minden helyen folyamatosan változik az időben. Továbbá, ez változó magasságú mivel a magassága változik, mint a légköri nyomás és a levegő hőmérséklete. Nyomás magasság mindig csökken, és csökken, és sűrűsége vele együtt. Hőmérséklet a magassággal, a mag csökken legalább az alsó rétegek (10-15 km) atmoszférában. De a hőmérséklet-csökkenés növekedést okoz sűrűsége. Ennek eredményeként az általános hatását a nyomás és a hőmérséklet a magassággal sűrűség általában csökken, de nem annyira, mint a nyomás. Átlagban, Európa számára ez egyenlő a felületén 1,25 kg / m 3; magasságban 5 km - 0,74 kg / m 3; 10 km - 0,41 kg / m 3; 20 km - 0,09 kg / m 3.
légnyomás változása a magassággal. barometrikus képletű
Törvény, amely szerint a légköri nyomás változása a magassággal?
Tegyük fel, hogy tudjuk, hogy a nyomás azonos szinten. Mi ez egyúttal egy másik szinten? Tekintsünk egy függőleges oszlop a levegő keresztmetszetű egyenlő eggyel, és válassza ki az oszlopot egy vékony réteg által határolt alsó felületének a magassága Z. és a fenti - a felszíni magassága (Z + dZ). Rétegvastagság Dz.
3.1 ábra - ható erők elemi térfogatú levegőt
Az alsó felületén a kiválasztott kötet elem szomszédos levegő aktusok a nyomóerő, amely felfelé irányul. A modul Ezen erő a megvizsgált felület egyenlő eggyel, és lesz a légnyomás P a felszínen. A felső felületén az elemi térfogat szomszédos levegőt cselekmények egy nyomóerő, amely lefelé irányul. A modul ezen teljesítmény P + dP az a nyomás, a felső határ. Ez a nyomás eltér a nyomás az alsó határ a kis méretű dp, ahol nem ismert előre, dp pozitív vagy negatív, akkor nem lesz nyomás a felső határ magasabb vagy alacsonyabb, mint az alsó határ.
Ami a nyomóerők, amelyek hatnak a oldalfalán a hangerő, akkor feltételezzük, hogy a légköri nyomás nem változik a vízszintes irányban. Ez azt jelenti, hogy a nyomás ható erők minden oldalon, hogy az oldalfalak, kiegyensúlyozott: a kapott nulla. Ez azt jelenti, hogy a levegő nem lesz gyorsítás, és nem mozdul a vízszintes irányban.
Szintén úgy vélik, egy térfogat eleme a gravitációs erő, és amely megegyezik a lefelé irányuló nehézségi gyorsulás g alkalommal a levegő tömege hozott mennyiségben. Ezért, amikor a függőleges rész egyenlő egység, a mennyiség megegyezik dz, a levegő tömege benne egyenlő ρdz, ahol ρ - levegő sűrűsége, és a gravitáció egyenlő gρdz.
Gρdz gravitáció és az erő a P nyomás a + dp lefelé irányul; vigye negatív előjellel. Felfelé irányuló nyomás P erő, akkor lesz egy „+” jel.
Az egyensúlyi állapot:
- (P + dp) + P - gρdz = 0
vagy dp = - gρdz (3.4)
Ez azt jelenti, hogy amikor felfelé mozog a légköri nyomás alá.
(3.4) képlet az alapvető egyenlet statikus légkörben.
-
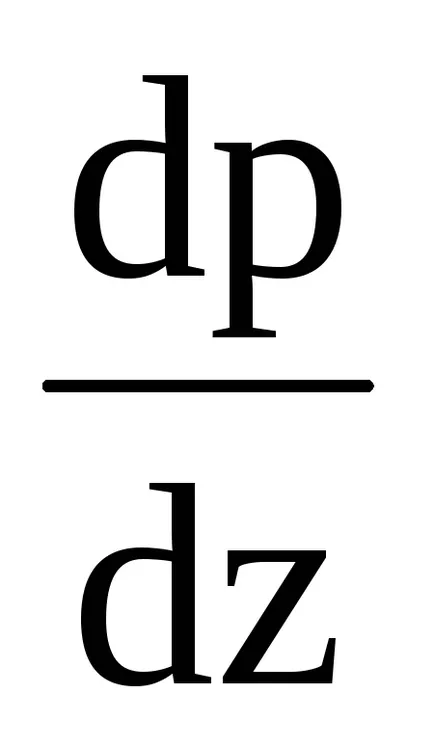
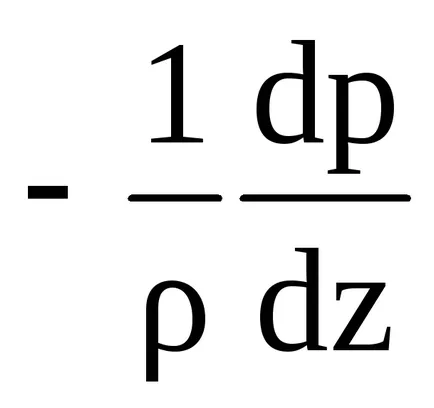
Az alapvető egyenlet fejezi állapotának statikus egyensúlyi a két erő, amelyek hatnak a tömegegységére levegő függőlegesen - függőleges nyomás gradiens és a gravitáció.
Ahhoz, hogy egy egyenletet a nyomás változása a végső növekménye magasság szükséges, hogy integrálja az (3.4) képlet tartományban szinten Z1 z2 nyomás P1 P2. Ebben az esetben a levegő sűrűsége ρ változtatható, a magasság függvényében.
Integrálja egyenletet (3.5)
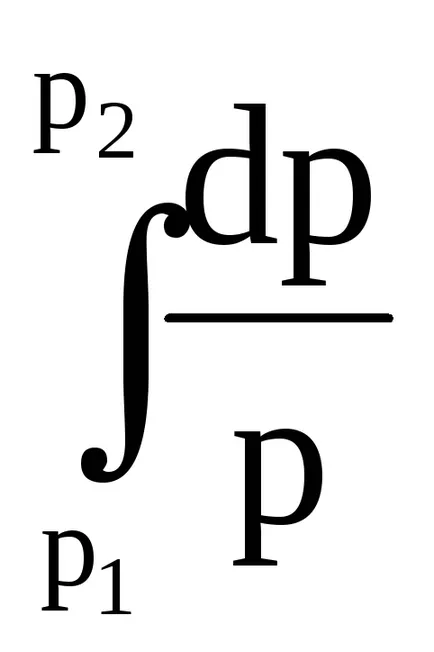
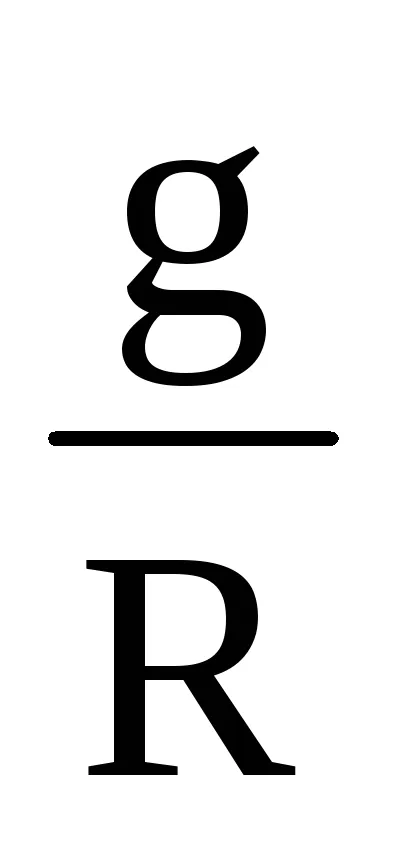
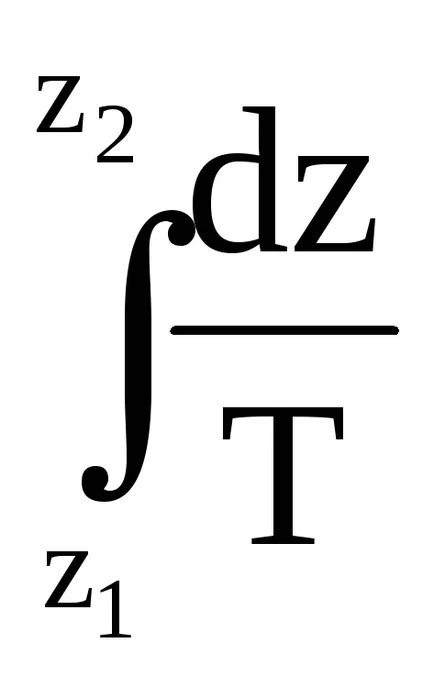
Hőmérséklet - változás mennyisége függ a magasságtól. De ez a kapcsolat nem lehet pontosan leírni matematikai függvény. Ezért figyelembe az átlagos érték Tm közötti hőmérséklet szintje Z1 és Z2. Ekkor az átlagos hőmérséklet kivinni az integrál jel.
ln
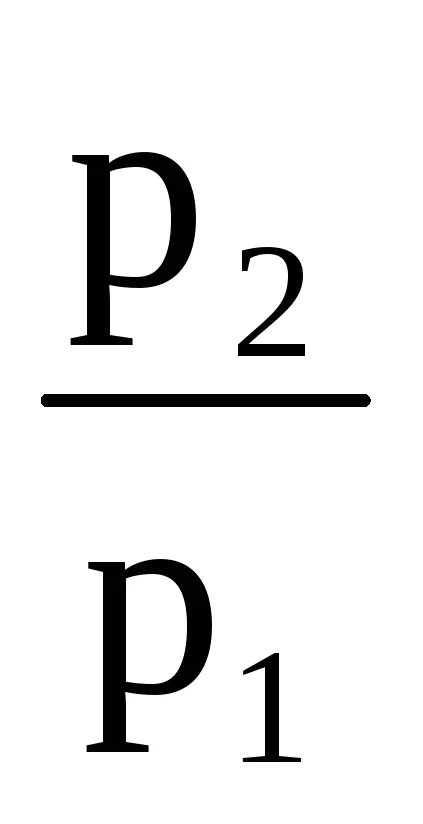
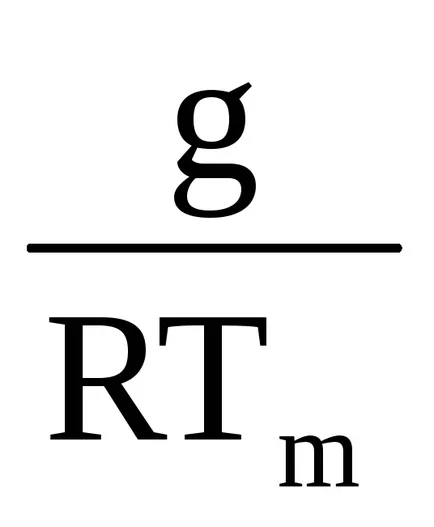
Potencirozására egyenlet 3.6, és azt kapjuk:
Egyenlet (3.7) nevezzük légköri képlet.
Ez a képlet azt mutatja, hogy a levegő nyomása változik a magassággal, attól függően, hogy a külső hőmérséklet.
Segítségével a barometrikus formula képes megoldani három probléma:
ismerve a nyomást egy szinten és az átlagos hőmérséklet a levegő réteg, megtalálja a nyomás a másik szinten;
ismerve a nyomást mindkét szinten, és az átlagos hőmérséklet a levegő réteg, talál egy szintkülönbség (barometrikus szintezés);
ismerve a szintkülönbség és a nyomás értékek számukra, hogy megtalálja azt az átlagos hőmérséklet a levegő réteg.
Abban az esetben, számítások a nedves levegő vesszük R érték a száraz levegő, szorozva (1 + 0,378)
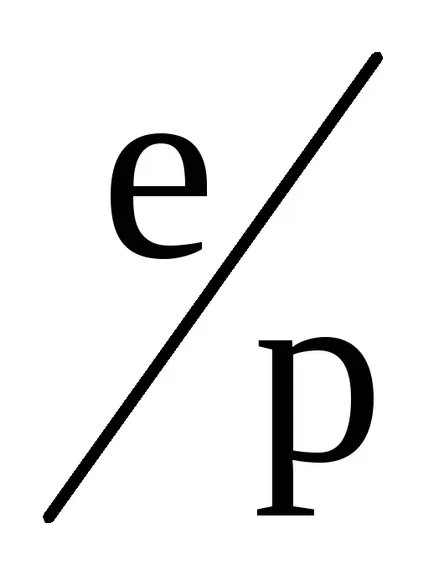
Azt, hogy gyakoroljon nyomást a tenger szintje fontos megvalósítási módja az első probléma. Ismerve a nyomás egy állomás magasságban található Z tengerszint feletti, és a hőmérséklet t ezen az állomáson, kiszámításához az első átlagos hőmérséklet a vizsgált állomás és a tengerszinten. Mert állomás szintjén hozott az aktuális hőmérsékletet, és a tengerszint felett - ugyanezen a hőmérsékleten, de nőtt olyan mértékben, hogy a levegő átlaghőmérséklete változik a magassággal. Átlagos függőleges hőmérséklet-gradiens a troposzférában vesszük egyenlő 0,6 ° C / 100 g
Így, ha egy állomás van egy magassága 200 m, és a hőmérséklet az ott 16 ° C-on, majd a tengerszint hőmérsékletet feltételezve, hogy egyenlő 17,2 ° C-on és az átlagos hőmérséklet lesz 16,6 ° C-on Ezt követően, a nyomás az állomáson és az átlagos hőmérséklet a kapott meghatározott nyomás a tengerszinten. Hoz nyomás tengerszinten van szükség, mert a felszínen időjárás térkép mindig alkalmazott nyomás csökken a tengerszint felett. Ez kiküszöböli a hatása eltérések magasságtól állomás a nyomás értékét és lehetővé válik, hogy meghatározzuk a vízszintes nyomás eloszlása.