2. fejezet Az egyenlet a halmazállapot
2.1. Termál és kalória egyenletei állam
A teljes száma termikus és termodinamikai egyenletek jármű állapota határozza meg a számát szabadsági fok, azaz a beleértve az hatással van a jármű az általánosított erők. Ezek az egyenletek empirikusan vagy módszerek a statisztikus fizika.
Egyszerű TC (száma szabadsági fokok, N = 2), amely egy generalizált erő mechanikai jellegű - davlenier. konjugátum külső parametruV. kölcsönhatás a környezet jellemzi csak egy külső paraméter változik a reakció, (generalizált koordináta) - obemomV és temperaturoyT (független paraméter). Ezután az egyensúlyi állapot a belső paraméterek: nyomás és a belső energiyuU lehet kifejezni funkcionális függőségek: p = p (V, T) - termikus állapotegyenlet és U = U (V, T) - kalorikus állapotegyenlet.
Termikus állapotegyenlet egy egyszerű TS ábrázolható formájában kapcsolat: F (P, V, T) = 0. Ez az egyenlet a termodinamikai állapotát a felület vagy felületek. Egy ideális gáz állapotegyenlet termikusan Clapeyron egyenlet: pV = MRT. ahol R - specifikus gázállandó.
Sostoyaniyaidealnogo egyenlet fűtőértékű gázt lehet beszerezni a Joule törvény: „Belső sistemyU termodinamikai energia T = const független obemaV:
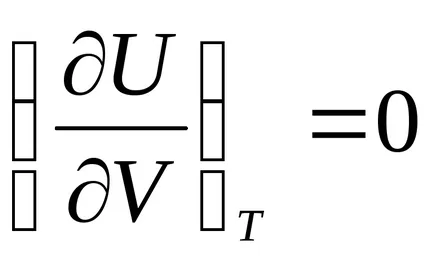
Differenciálás egyenlet U = U (V, T), kapjuk:
,
ahol
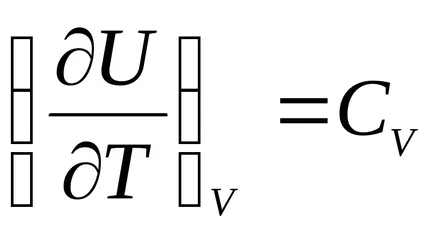
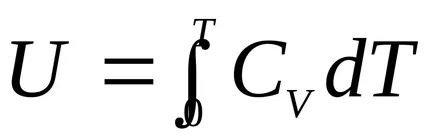
azaz A belső energia az ideális gáz egy hőmérséklet függvénye:
.
Kalóriatartalmú és termikus állapotegyenlet az ideális gáz is előállíthatók a molekuláris-kinetikus fogalmak.
2.2. Thermal állapotegyenlet az ideális gáz
Formálisan meghatározott gazmozhno ideális gáz engedelmeskedik Clapeyron egyenlet:
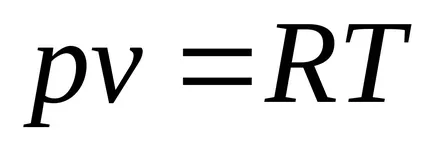
Egy fizikai szempontból ideális gáz - gáz, amelynek molekulái mentesek térbeli kiterjedése (gáz térfogatát molekulák az edényben - Vmol< , ahol k = 1.380658 (12) 10 -23 [J / K] - Boltzmann állandó;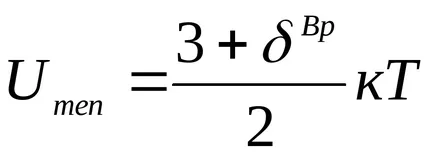
Ahhoz, hogy 1 kg: pv = RT. ahol a képletben R, J / kgK - specifikus gázállandó típusától függően a gáz, p. Pa; v. m 3 / kg; T K.
1 mol:
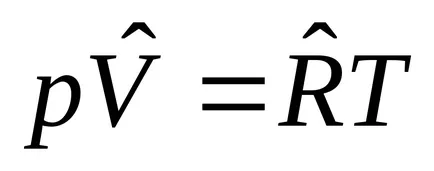

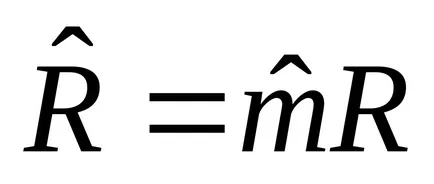


5. 1m 3:
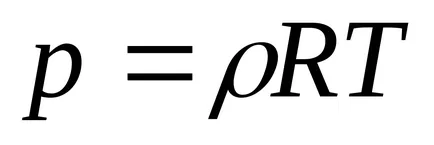
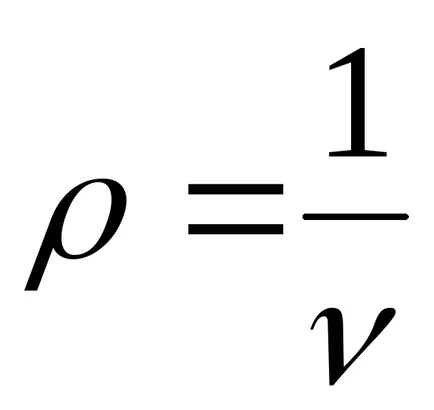
6. 1m 3:
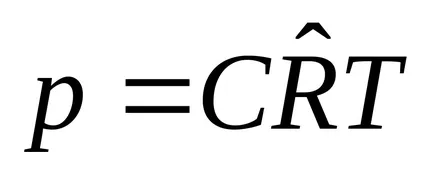
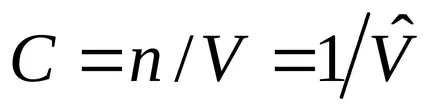
2.3. Hőállapot egyenlet reális gázok
A specifikus formája termikus egyenletet függ aggregációs állapotától és az a fajta anyag. Ez most jól fejlett állapotegyenletre valódi gázok csak. Az állapotegyenlet kondenzált anyagok rendkívül ritka, mert nem szükséges a gyakorlati számításokban.
Az egyenlet alakjának állami valódi gázok erősen függ a részecskeméret és azok szerkezete és a természet a kölcsönhatás közöttük. A potenciális energia kölcsönhatás Udvuh molekulák függ a távolság a központ -r. t.e.U = f (r). reális gázok molekulák véges méretű és vonzzák egymást olyan erővel, amely csökkenésével növekszik közötti átlagos távolság molekulák, ellentétben az ideális gázokra kotorogoU y (r) = 0.
Számítások a potenciális energia U többnyire a Lennard-Jones:
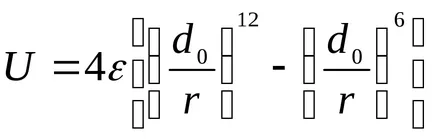
elnevezések értékek

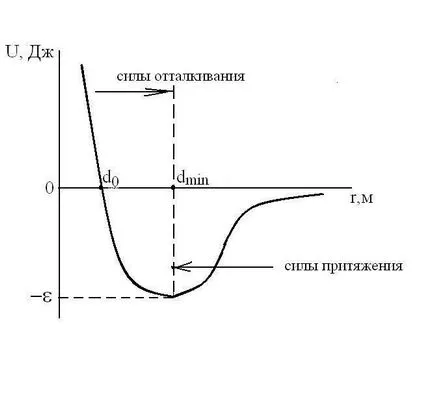
Kölcsönhatás erők közötti molekulák
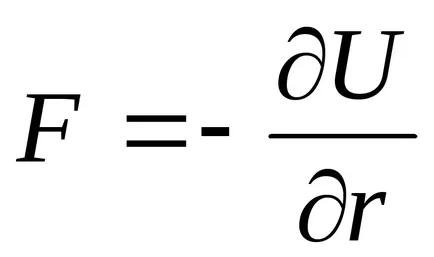
1 / r 6. szilárdság és vzaimodeystviyaF
1 / R 7. Kis rasstoyaniyr (erélyes molekulák megközelítés) U
Összehasonlításképpen megjegyezzük, hogy a Coulomb kölcsönhatás potenciális U
1 / r 2. Így, Van der Waals erők növekedésével csökken rasstoyaniyar részecskék közötti sokkal gyorsabb, mint a Coulomb-erő. Ezért az állami egyenlet reális gázok általában nem alkalmasak a plazmában. A plazma állapotegyenlet származik külön (Debye).
Kölcsönhatás erők távolságtól függően a részecskék között (F = f (R)) használunk, hogy kiszámolja a együtthatókat a különböző egyenletek az állami és a tényleges plazmagáz.
A legegyszerűbb állapotegyenletet valódi gázok egyenlete van der Waals (1873) (Jelenleg több mint 150 empirikus egyenletek). Ez az egyenlet a következő formában:
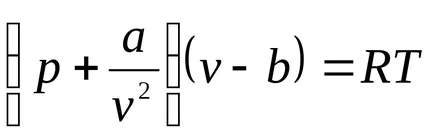
ahol b - a korrekció a molekuláris térfogat, A / V 2 - korrigáltuk molekuláris vagy belső nyomás által meghatározott kölcsönös vonzás a gázmolekulák. Konstantya és b függ a gáz típusától (a anyag jellegét).
Folyadékok tárolására, ez az egyenlet hadilábon a kísérleti adatokkal. Ez az egyenlet azt mutatja, az esetleges két fázis arra enged következtetni, hogy van egy kritikus pont. Ha az attribútum paraméterek p, T, v, hogy a kritikus parametrampk, Tc, vk a kritikus pont a fázisdiagram és azonosítani
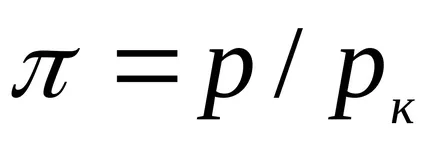
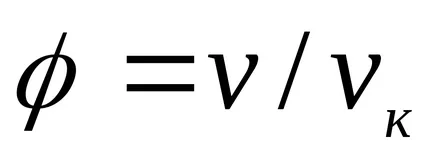
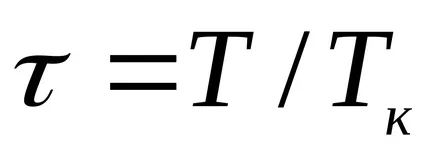
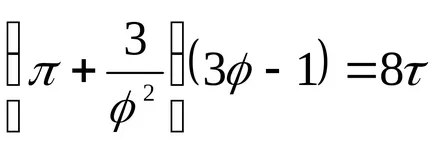
amely kifejezi a törvény megfelelő államokban.
Megfelelő állapotok nevezzük államok különböző anyagok, amelyek ugyanazt a felsorolt paraméterek




A vadervaalsovskogo gáz Rk = 2,67.
Eltérés reális gáz tulajdonságai az ideális gáz kompresszibilitási tulajdonságokkal jellemezhető nagysága a kompresszibilitási tényező vagy
Egy ideális gáz Z = 1. Az igazi gazaZ ≠ 1. A nagysága a kompresszibilitási tényező függ a nyomás, hőmérséklet és a gáz típusa és lehet nagyobb vagy kisebb, mint az egység függően ezeket a tényezőket.
Az egyenletek az állami nyerhető egy igazi gáz, figyelembe véve a kölcsönhatása a részecskék. Ezek az egyenletek az úgynevezett Virial állapotegyenlet, amely V - formában a következők:
,
ahol A (T) A (T) C (T) - az első, második és harmadik Virial együtthatók, amelyek függnek a hőmérséklettől. A p-formájú Virial egyenlet a következő formában:
Az együtthatók A (T) A (T) C (T) kapcsolódó együtthatók A '(T), a B' (T) C * (T).
Az első együttható A (T) úgy határozzuk meg, a bináris ütközések a részecskék, a második együttható B (T) - tripla ütközések részecskék stb Egyidejű ütközése nagyszámú részecskékre - nem valószínű. A legfontosabb szerepet játszott bináris ütközések részecskék. Ha a számla jobb oldalán a Virial egyenletek mentése csak két szempontból. Egy példa ennek az egyenletnek az egyenlet a van der Waals erők. Az együttható A (T) úgy határozzuk meg integrálásával bináris ütközés lehetséges. Minél nagyobb a nyomás, annál nagyobb a kifejezések száma a jobb oldalon a Virial egyenlet figyelembe kell venni.
Hőállapot egyenletek a különböző anyagok vannak beállítva a kísérleti adatokat a kompresszibilitási Z = p
