A hengereket a másodrendű

a) Egy elliptikus henger

(14) egyenletben nem tartalmaz változó. Az egyenletben a sík (14) meghatároz egy ellipszis félig tengelyek és. Ha a pont fekszik ezen ellipszis, majd bármely pontján a felületen (14). A készlet az ilyen pontok olyan felülete által leírt egy egyenes vonal, a tengellyel párhuzamos, és metsző az ellipszis

Ellipszis (14) nevezett útmutató sorban a felület, és az összes lehetséges helyzetében az említett mozgó egyenes - generátorok.

Általában a felület által leírt egy egyenes vonal, párhuzamosak maradnak néhány adott irány és a keresztező ezt a vonalat nevezzük hengeres. A felület (14) látható a Fig.49.

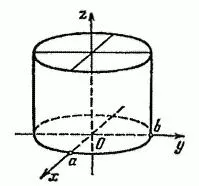
b) hiperbolikus és parabolikus hengerek

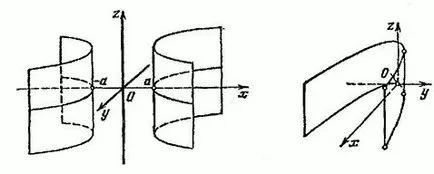
Ebben az esetben a vezető felületek vannak hiperbola vonalak és parabola generátorok és - közvetlen párhuzamos tengelyen átmenő és a hiperbola vagy parabola síkon. A felület (15) és (16) ábrán mutatjuk be. 50 és 51.

c) párhuzamos és egymást metsző síkok. Direct.

Egy felületet (17) terelők egyenes vonalak

Ezért, a felület (17) van egy pár egymást metsző síkok. Egyenletben felületek (18) és (19) hiányzik a két koordináta. (18) egyenlet a síkban van egy pár sort.

Ha veszünk bármilyen, majd a pontok megfelelnek a (18) egyenletet, így a felület (18) egy pár párhuzamos síkok.

(19) képlet írja le egy repülőgép, mivel ez az egyenlet teljesül, bármilyen típusú pont, és minden sokaságának, amelynek sík.

Is felfogható, mint egy útmutató bármely sík vagy generátorok vonalak tengelyével párhuzamosan vagy tengelyére és áthalad a vonalon.

(20) egyenletben megfelel bármely pontján, és bármilyen. Ezért, (20) jelentése egy egyenes vonal, nevezetesen, a tengely.